SCSP-SFDC/77/AEn/CP14
by
R.G. Hechanova
FAO/UNDP Brackishwater Aquaculture Development and Training Project
Manila, Philippines
1. INTRODUCTION
The physical make-up of most aquaculture projects is in general, inadequate insofar as they are engineering structures. Most of these structures are not designed to the requirements for which they are constructed and so, they have fallen short of expectations. Problems therefore arise.
The importance of the basic principles is recognized by a discussion of the principles particularly of hydraulic engineering and of soil mechanics which deal with the properties, characteristics and behaviour of soils. These two subjects are rich in the variety and interest of their practical applications in the field. Fortunately, with these technologies have come new materials and improved methods for fishpond construction.
2. LEVEE DESIGN AND CONSTRUCTION
The design and construction of earth dikes deserve much attention owing to many variants encountered in the site. Due to high cost of development, actual dike construction often violates good engineering practice. When failure occurs, the cost of the failure is many times more than the cost of the original construction. The fish farm engineer because of poor construction supervision and sub-standard practices must allow for a higher factor of safety.
Limited consideration is given to the choice of materials to use for dikes; the trend is to use what poor material is readily available near the proposed dike areas. The fish farm engineer may avoid these difficulties by any one of the several procedures:
For fish farm structures the properties of soils that are of primary importance from a practical standpoint are permeability, compressibility and shear strength. These will be discussed in the paragraphs that follow.
Clearing the path of the dike by removal of vegetation, mangrove stumps and big roots is necessary. The uprooted stumps will be placed on the outer slope of the dikes to serve as slope protection. For large-scale development, a low ground pressure tractor with a special blade may be used in felling, uprooting, removal of vegetation and in removing bad topsoil. Where springs or upwelling of underground water is encountered along the line of the dike, special cross-section designs will have to be incorporated, otherwise dike alignment will have to be changed. The presence of stumps in the dike foundation can cause problems of leakage in the future.
In actual dike construction, the provision for a clay puddle trench should be strictly followed. This core wall is constructed in order to prevent the passage of water through the embankment and sometimes as a barrier to the passage of burrowing animals. Materials for core walls include clay puddle, concrete and plastic sheets. The clay puddle consists of a mixture of clay and sand with water. The core wall is placed slightly upstream from the center of the proposed levee and extends above the level of the highest tide (Figure 1).
For pond soils which are unusually soft and compressible, or consist of organic matter to a somewhat relatively shallow depth, it is frequently economical to remove these undesirable soils and then backfill with select materials compacted in layers.
If the cost of excavating the bad soil and filling with a suitable one is prohibitive, the soft soil can be improved by a process of consolidation. The length of time needed to attain permissive settlement however, is long and consolidation tests are not feasible. Time-dependent consolidation of the soft foundation material results due to the weight of the dike material. This amount of settlement is corrected later on by increasing the dike height. Overbuilding the dikes provides for consolidation.
Since fish-farm dikes have shallow water depths, they are not subject to high horizontal thrust and failures due to sliding and/or overturning. It is customary, however, to design the cross-section with a width of base enough so that the resultant of all forces (water pressure and weight of fill) will pass through the base within the middle third. This condition is attained when the cross-section is designed for seepage, which topic is discussed later in this presentation.
Wave action on dikes near the coastline is minimized and damage is prevented by providing a buffer zone inland from the shoreline. In other words, the vegetation in this area is preserved. Portions of the main dike facing the sea may be reinforced with an armor coat of stone rip-rap or other suitable forms of sea wall protection.
3. REQUIRED SOIL TESTS AND DESIGN CONSIDERATIONS
A complete programme of soil exploration should be included in the pre-development stage. Visual inspection must precede laboratory tests of soils. For practical purposes, a test rod of an iron pipe l-inch in diameter is driven and turned under each blow, by means of a pipe wrench. Very meager information is obtainable by this method although it may reveal the depth of soft strata. As the pipe is driven, additional sections of 1.2 m (4 feet long) are screwed and the upper section fitted with a drive cap. If the rod stops with a dull ring, it has probably struck hard clay. The rod may then be withdrawn by level and chain.
A procedure for determining the characteristics of soils at the site is the standard penetration test which is conducted in connection with soil sampling using the split spoon (Gaylord and Gaylord, 1969). The use of the Vane auger (Gaylord and Gaylord, 1969) to record the consistency of clay is also common. This method determines the consistency of clay as soft, medium or hard.
The soil texture is investigated by mechanical analysis based on disturbed samples. This test is done by the Bureau of Soils or by the Materials Control Laboratory of the Philippines, Department of the Public Highways. The percentage of sand, silt and clay gives the textural grade of the soil by using the soil classification chart (Figure 2). The result of the mechanical and, of the wet soil analysis for the colloidal portions, are plotted on the soil grain distribution curve (Figure 3). The curve shows a properly graded soil in which coarse fractions are predominant and a soil in which fine fractions are predominant.
A knowledge of the properties, characteristics and behaviour of soils is very important to persons who are involved with the design and construction of structures involving soils. Prior to discussion of analysis regarding the design of levees, it is desirable to become familiar with some of the physical properties of the soil. No two soil deposits are the same and so samples taken from one area are not truly representative of the overall area. Many theories of soil mechanics developed through research are based on assumptions and the validity of these theories are no better than the assumptions made. In most cases, field or laboratory tests must be performed.
For descriptive purposes, three broad groups of soils are considered.
Granular soils such as sand and gravel. A soil that is entirely composed of gravel is designated gravel. A soil that is composed of sand and gravel is designated as sand-gravel.
Fine-grained soils including inorganic silts and clays. A soil is clay if it can be made plastic by adjusting its water content and if it exhibits considerable strength when air dried. In general, fine-grained soil consists of a combination of silt and clay and these terms are used in qualitative rather than a quantitative sense. Thus clay-silt designates soil that is predominantly silt-like, but exhibits clay-like properties.
Organic soils including peat, muck, organic silts and organic clays. Organic soil designates these soils containing an appreciable amount of decayed animal and/or vegetable matter in various states of decomposition. These soil types should be viewed with suspicion as foundation materials since they reduce the load sustaining quality of the soil, are easily compressible and have low shearing strength.
The terms gravel, sand, silt and clay thus form the basic elements of a soil name. Soil grains vary in size from a certain maximum down to microscopic size. How these different particle sizes are distributed in a soil mass is of importance to the soil engineer in the construction of dikes where the earth is used as a construction material that must satisfy dike specifications for impermeability, maximum density and structural fractions. The grain size determination is known as mechanical analysis and uses standard sieves of varying sizes, down to 0.074 mm corresponding to the 200-mesh sieve. Particle size distribution smaller than 0.074 mm are determined by methods based on the speed of sedimentation of the particles in a liquid. This method is known as the wet analysis of soils, the most common of which is the hydrometer method. The combined results of the mechanical and wet analysis are then represented in a grain size distribution curve, as shown in Figure 3. The ordinates to the graph are percentage of grain finer than any given diameter plotted on an arithmetic scale, the abcissa plotted on a logarithmic scale, representing the diameter. From the curve the effective size is the largest diameter of the grains comprising the finer 10% of the soil. The value of the uniformity coefficient is clearly explained. It should be noted that the more uniform the grain size distribution is, the steeper would the curve be, and theoretically, a uniform soil has a uniformity coefficient of unity. Soils having values of uniformity coefficient nearer to unity are those which are pervious and compressible and therefore are not good diking material.
The effect of changes in water content in the soil and that of the behaviour of the change is highly significant as they affect the physical characteristics of the soil. A given soil with high water content has the properties of a liquid in that it flows freely; acquires the shape of the containing vessel and will offer no resistance to shear. In this condition the soil is in a liquid state. The minimum water content at which the soil will flow under its own weight is the liquid limit (LL) of the soil. If the water content is decreased by evaporation, the soil will cease to flow and it will lose its liquid characteristics. It will not deform by its own weight but it can be deformed without rupture. Under this condition of water content, the soil is said to be in the plastic state. If the water content is further decreased, the plastic properties are gradually lost and the soil crumbles under external load. The soil in this condition is in the semisolid state. Further decrease in the content will cause the color to change and the sample becomes hard. The soil in this condition is in the solid state. The plastic limit (PL) of the soil is definied as the minimum water content at which the soil can be rolled into threads 1/8-inch in diameter without breaking. At water contents between the liquid limit and the plastic limit the soil is in the plastic state and the range between these water contents is called the Plasticity Index (PI) and is expressed as the difference between the liquid and plastic limit as an abstract number. The moisture content at which further loss of water does not cause a decrease in the volume of the soil is called the Shrinkage Limit (SL) and the range between the plastic and the shrinkage limit is called the Shrinkage Index (SI).
From the above discussion, it can be said that soils with a relatively high value of shrinkage and plasticity indices are good material.
It is well known that the volume and density of the soil changes when earth is excavated, hauled, placed and compacted. When the volume of earth increases because of loosening this increase is defined as swell expressed in percent of the original undisturbed volume. If earth removed from a one cubic meter hole is found to have a loose volume of 1.25 cubic meter, the gain is 0.25 cubic meter and the swell is 25%.
When earth is placed in a fill and compacted it will have a smaller volume than its original condition. This reduction is a result of an increase in density and is termed as shrinkage, expressed as a percent of the original undisturbed volume. Thus if the one cubic meter of loose earth is found to have a compacted volume of 0.9 cubic meter, the loss in volume is 0.1 cubic meter and the shrinkage is 10%. In dike designs and earthwork computations, the percent shrinkage is computed if the undisturbed and compacted density are given and percent shrinkage S, equals
| S (shrinkage) | = |  |
| = | % shrinkage |
Representative soil samples are collected and tested. One of these tests is the determination of the optimum moisture content which is expressed as percent of water content that will permit the soil to be compacted to the maximum density with the least effort. Figure 4 shows the moisture and maximum density relationship and also the density and permeability relationship. The curves show that there is a certain water content for a soil at which maximum density can be attained. Also at that maximum density, the soil is resistant to seepage. This is very important and cannot be disregarded, although actual practices in dike construction is such that compaction is done under conditions of high water content, usually above the “optimum” value.
In order to have a high density dike, the soil should be placed in horizontal layers along the dike and the soil allowed to stand until some of the water is evaporated so that the moisture content approaches that of “optimum” (about 16% for clay). Compaction is then done by whatever means available.
Table 1. Typical values of optimum moisture content and density of various soils
| Description | Range of dry unit weight (lbs/cu.ft.) | Range of optimum moisture content (percent) |
| Sand-silt clay mix with plastic fines | 110 – 130 | 15 – 11 |
| Clayey sands, sand-clay mix | 105 – 125 | 11 – 10 |
| Inorganic silts and clayey silts | 95 – 120 | 24 – 12 |
| Inorganic clay | 95 – 120 | 24 – 12 |
| Organic silts | 80 – 100 | 33 – 21 |
| Inorganic clay of high plasticity | 75 – 105 | 36 – 19 |
| Organic clays | 65 – 100 | 45 – 21 |
Shown in Table 1 are values of standard optimum moisture content and density for various soils in fish farms. Optimum moisture content is usually 2 to 5 percent less than the plastic limit of the soil.
Table 2. Typical compaction requirement based upon standard Procter Compaction Test for fish farm soils. (AASHO T99, ASTM D698 or Brt Std 1377)
| Purpose of Fill | Density required fine-grained soil | Suggested range of moisture content-dry to wet of optimum |
| Fills requiring nominal amount of strength and incompressibility as earth dikes | 90 % | -3 to +3 |
Shown in table 2 is a typical compaction guide based on the Proctor Test. With the start and during construction, field density tests should be made. Satisfactory compaction is attained if 2/3 of all field values fall within a range of within 2–3%. Unsatisfactory compaction is evidenced where only 2/3 of all field values fall in a range of +5%.
4. STABILITY OF SIDE SLOPES
The stability of the side slopes of an earth dike (and of canals) in homogenous deposits of cohesive soil such as clay can be analyzed by the use of the graph of Figure 5. Given the proposed depth of cut or the height of the dike, H; the overall depth to the firm horizontal layer, ndH and the unit weight of the soil, the cohesive strength required to provide a factor of safety of 1 can be computed from the equation,

| where w | = | unit weight of the soil, lbs/cu. ft. |
| Ns | = | stability factor as determined from Figure 5 |
| H | = | height of cut or embankment, feet |
| creqd | = | required cohesive strength, lbs/cu. ft. |
The graph of Figure 5 shows the relationship between the stability factor Ns, slope angle, θ and depth factor nd for a purely cohesive soil (clay) in which the internal angle Æ = Od. The value creqd as determined from the preceding formula can be compared with the available cohesive strength of the soil, for a factor of safety of 1. The factor of safety will depend upon several factors as, how much threat to life and property there is, reliability of the soil characteristic data and probability of live loads on the embankment. A factor of safety of 2 is normally required.
The recommended safe value of c, pounds per sq. ft. (psf), for clay ranges from 40 for the very soft to 100 for the hard consistency. For a side slope of 1:1, the angle θ is 45° and for clay in the wet dike condition, the unit weight w, is 120 lbs/cu.ft. The available cohesive strength is assumed to be about 250 psf. Solving for the height H for a dike on a stable foundation base, gives
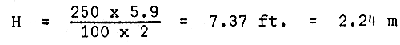
The stability factor, Ns was obtained from Figure 5 to be 2.54
The foregoing presentation gives the following procedures in design of embankments:
undisturbed soil samples should be taken and brought to the laboratory for analysis of:
unconfined compression test (which is used in determining the compressive stress that will result in failure of a cohesive soil sample, from which the value of cohesive strength, c is ½ the compressive stress at failure
the depth of the firm foundation from ground level should be determined;
a vane shear test to roughly determine the cohesive strength of clayey soil should be conducted;
the computation of slope stability should be made as indicated.
5. HYDRAULICS
5.1 Design of open channel cross sections for uniform flow as applicable to trapezoidal earth canals in fish farms
The typical problem in the design of (trapezoidal) earth canals is to determine the most economical proportion of the cross-section that requires a minimum of excavation. Flow will be assumed as steady flow, although this condition is not so in tide-fed fish farms.
Under ordinary field conditions where there are number of variables the author has settled on the use of a few accepted formulas. These formulas are used repeatedly so the reader will become acquainted with the various coefficients which give fair and reasonable results for the locality served.
Philippine practice in this field is substantially influenced by American textbooks and equipment in which the English system of measurements are used. The English and Metric systems are presented.
The importance of the basic principles is recognized in order that the reader can deal with problems that may arise in practice. Tables and charts are presented and their use explained.
In practice the economics of canal design is affected by the following factors:
If the cross-sectional area, A is to be a minimum, the velocity, v is to be maximum. Scouring of the erodible canal bed will occur when velocities are high.
Canal capacity can better be increased by widening than by deepening the channel.
The minimum value of the canal area A includes overburden. Therefore, minimum A does not imply minimum excavation.
The cost of excavation is not solely dependent on the amount of earth removed. Considerations as earth disposal and/or transfer may be important as earth material volume. The relationship between width to depth must be considered as the ratio varies widely.
Side slope could vary if design consideration includes design for minimum seepage.
Seepage or sub-surface runoff that contribute to canal flow will not be considered as this will be treated separately.
The dimensions and formulas in this paper refer to uniform flow, which occurs when the canal cross-section and slope are constant throughout the canal length. The presence of canal control structures which affect flow is not considered.
A basic hydraulic formula developed by R. Manning for determining the flow of water particularly in open channels is written as follows:

in which
| Q | = | discharge in cubic metres per second |
| A | = | cross-sectional area of flow, in square metres |
| V | = | mean velocity of water, in metres per second |
| S | = | slope of the canal bed in metres per metre |
| R | = | hydraulic radius in metres, defined as the ratio of A to P, in which P is the wetted perimeter |
| n | = | coefficient of roughness, which for earth canals is 0.0225 (new and well-maintained canals) |
The solution of Manning's equation introduces a “K” value as:
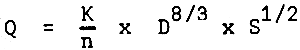
where K = discharge factor and for trapezoidal channels,
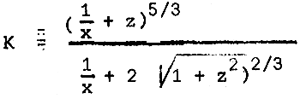
| where | z | = | D/b = ratio of depth of water to bottom width of channel and |
| z | = | canal side slope, ratio of horizontal to vertical. |
Table 3 gives values of K corresponding to D/b for common side slopes used in practice.
Table 3. K values for trapezoidal channels in the Manning's formula
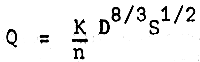
| D/b ratio | SIDE SLOPES | ||
| 1:1 | 2:1 | ||
| 0.20 | 5.026 | 5.390 | 5.720 |
| 0.21 | 4.798 | 5.161 | 5.491 |
| 0.22 | 4.589 | 4.952 | 5.282 |
| 0.23 | 4.401 | 4.764 | 5.094 |
| 0.24 | 4.226 | 4.589 | 4.925 |
| 0.25 | 4.064 | 4.427 | 4.764 |
| 0.26 | 3.916 | 4.286 | 4.623 |
| 0.27 | 3.781 | 4.152 | 4.488 |
| 0.28 | 3.654 | 4.024 | 4.360 |
| 0.29 | 3.532 | 3.909 | 4.246 |
| 0.30 | 3.425 | 3.795 | 4.138 |
| 0.31 | 3.324 | 3.694 | 4.037 |
| 0.32 | 3.230 | 3.600 | 3.943 |
| 0.33 | 3.142 | 3.512 | 3.855 |
| 0.34 | 3.055 | 3.425 | 3.768 |
| 0.35 | 2.981 | 3.351 | 3.694 |
| 0.36 | 2.907 | 3.277 | 3.620 |
| 0.37 | 2.833 | 3.203 | 3.546 |
| 0.38 | 2.765 | 3.135 | 3.479 |
| 0.39 | 2.705 | 3.075 | 3.418 |
| 0.40 | 2.644 | 3.014 | 3.358 |
| 0.41 | 2.590 | 2.960 | 3.304 |
| 0.42 | 2.537 | 2.907 | 3.250 |
| 0.43 | 2.483 | 2.853 | 3.196 |
| 0.44 | 2.436 | 2.806 | 3.149 |
| 0.45 | 2.388 | 2.759 | 3.102 |
| 0.46 | 2.341 | 2.718 | 3.061 |
| 0.47 | 2.301 | 2.671 | 3.021 |
| 0.48 | 2.261 | 2.631 | 2.974 |
| 0.49 | 2.220 | 2.590 | 2.940 |
| 0.50 | 2.187 | 2.557 | 2.900 |
| 0.51 | 2.146 | 2.523 | 2.866 |
| 0.52 | 2.113 | 2.489 | 2.833 |
| 0.53 | 2.079 | 2.456 | 2.799 |
| 0.54 | 2.052 | 2.422 | 2.765 |
| 0.55 | 2.018 | 2.388 | 2.738 |
| 0.56 | 1.991 | 2.362 | 2.705 |
| 0.57 | 1.958 | 2.335 | 2.678 |
| 0.58 | 1.931 | 2.308 | 2.651 |
| 0.59 | 1.904 | 2.281 | 2.624 |
| 0.60 | 1.884 | 2.254 | 2.597 |
Manning's formula indicates that the cross-section of greatest hydraulic efficiency is the one that, for a given shape and area, has the maximum capacity Q and therefore the shortest wetted perimeter P. For a trapezoidal section, a general expression for b can be written expressed in terms of D and side slope, z, as
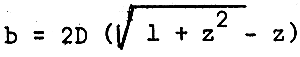
Table 4. Values of bed width, b for different values of depth D, and side slope based on the formula
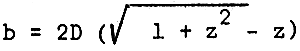
| Depth of water, meters | SIDE SLOPE | |||
| 1:1 | 1.75:1 | 1.5:1 | 2:1 | |
| 0.50 | 0.414 | 0.265 | 0.302 | 0.236 |
| 0.75 | 0.621 | 0.397 | 0.453 | 0.354 |
| 1.00 | 0.828 | 0.530 | 0.604 | 0.472 |
| 1.25 | 1.035 | 0.662 | 0.755 | 0.590 |
| 1.50 | 1.242 | 0.795 | 0.906 | 0.708 |
| 1.75 | 1.449 | 0.927 | 1.057 | 0.826 |
| 2.00 | 1.656 | 1.060 | 1.208 | 0.944 |
| 2.25 | 1.863 | 1.192 | 1.359 | 1.062 |
| 2.50 | 2.070 | 1.325 | 1.510 | 1.180 |
| 2.75 | 2.277 | 1.457 | 1.661 | 1.298 |
| 3.00 | 2.484 | 1.590 | 1.812 | 1.416 |
Bed width, b for a main supply canal, shall not be less than the width of the main control gate, as determined prior to the design of the main canal.
For a given canal section, the slope of the canal bed determines whether the velocity of flow is silting or scouring tractive. It is desirable that velocities in earth canals be high enough to transport the silt particles during drainage without being high enough to produce erosion of the bed and side slopes. During flooding, the flow is sluggish due to a positive canal grade at inflow of tidal water. This silt-laden tidal water in the main canal is partly freed of silt before the water goes into the pond through the secondary gates. Removal of these silt particles is necessary thus, the slope shall be such that there is silting velocity at inflow and that there is transport velocity during drainage.
Values of maximum and permissible velocities are shown in Table 5.
Table 5. Permissible canal velocities for different soil types
| Soil type | VELOCITY | |
| ft/sec. | m/sec. | |
| Fine sand | 1.5 – 2.5 | 0.46 – 0.76 |
| Silt | 2 – 3 | 0.61 – 0.91 |
| Loam | 2.5 – 3.5 | 0.76 – 1.06 |
| Clay | 3.75 – 5 | 1.14 – 1.52 |
5.2 Procedure for design of a trapezoidal earth canal by the use of tables
Determine the discharge Q cubic metres per second. This is calculated depending upon the following:
adequacy for drainage especially in times of flood or heavy rainfall.
The desired depth D of water in the canal is determined according to:
depth required if canal has the function of regulating the water within the farm if soil improvement by leaching is to be done.
The value of canal bed width “b” is taken from Table 4, the canal side slope assumed and canal depth D as known from (ii). Canal bed width “b” is equal to or more than the width of the main control gate.
Solve for the ratio of D to b. Table 3 gives “K” values for known D/b ratios and canal side slopes.
Determine the slope S from Table 6, for required velocity, v at given depth D and permissible velocity values as obtained from Table 5.
Compute this value with Q using the formula 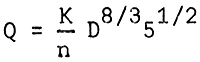
Table 6. Values of slope for different velocities V and depth, D
| Depth, D | V E L O C I T Y, m/sec | |||
| Fine sand | Silt | Loam | Clay | |
| V = 0.76 | 0.91 | 1.06 | 1.52 | |
| 0.50 | .001242 | .001780 | .002515 | .002415 |
| 0.75 | .000722 | .001036 | .001405 | .002891 |
| 1.00 | .000492 | .000706 | .000958 | .001971 |
| 1.25 | .000366 | .000525 | .000712 | .001465 |
| 1.50 | .000287 | .000412 | .000559 | .001150 |
| 1.75 | .000234 | .000335 | .000455 | .000937 |
| 2.00 | .000196 | .000281 | .000381 | .000784 |
| 2.25 | .000167 | .000240 | .000326 | .000670 |
| 2.50 | .000145 | .000208 | .000283 | .000582 |
| 2.75 | .000128 | .000184 | .000249 | .000513 |
| 3.00 | .000114 | .000163 | .000222 | .000457 |
For a trapezoidal section designed for maximum hydraulic efficiency,
| where R | 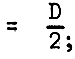 |
S |  |
The slope of the canal bed can be calculated for a given section and velocity. Manning's formula can be transposed to the following expresion; for slope,
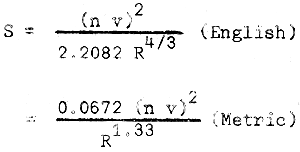
and for n = 0.0225
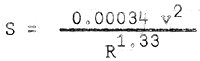
Slope S varies as the square of the coefficient “n”, slopes computed are likely to show variance from actual conditions.
For example, a canal section of depth, D equal to 1.00 metre and a side slope of 1:1 requires that “b” be 0.828 metres. For clay in which the permissible velocity is 1.52 metre/sec., and n = 0.0225, the required slope of the bed from Table 6 would be 0.00197.
6. CONCLUSIONS
It is hoped that because of increased awareness of the problems concerning engineering in the aquaculture industry, subsequently a manual on all subjects in aquaculture engineering be developed. An outline is presented as a guideline for development. This outline includes the following items.
6.1 Practical design procedures for fish farm structures. The use of charts, tables and nomograms should be handy for a non-engineer, but competent supervisor.
6.2 Construction specifications giving detailed description of aquaculture projects should be written so as to be easily understood by the layman.
6.3 A comprehensive study of equipment and implements used in brackishwater fish farms. These are the items which could generally be used in construction, maintenance, operation and management, whether for small or large-scale development.
6.4 Construction methods which are considered best and most economical for practice in the countries of the South China Sea Region.
6.5 A listing of equipment used in field and laboratory tests and detailed descriptions of the standard procedures for each test.
7. REFERENCES
Gaylord, C.N. and E.H. Gaylord, 1969 Structural engineering handbook, Section 5, Soil mechanics and foundation, pp. 5–18 to 5–23, and Section 6, Soil exploration, pp. 5–31 to 5–37. McGraw Hill Book Co., Inc.
Karol, R.H., 1955 Engineering properties of soils. Prentice-Hall, Inc. Civil Engineering Series, 567p.
King, H.W., et al, Hydraulics. John Willy and Sons, 5th Ed., pp. 255–57
Peurifoy, R.L., 1956 Construction planning equipment and methods. McGraw Hill Book Co., Inc., 696p.
Tang, Y.A., 1976 Planning, design and construction of a coastal fish farm. FAO Technical Conference in Aquaculture, Kyoto, Japan, 26 May – 2 June 1976. FIR:AQ/Conf/76/E67: 27p.
Urquhart, L.C., 1940 Civil Engineering Handbook. McGraw Hill Book Co., Inc., 2nd Edition, 896p.
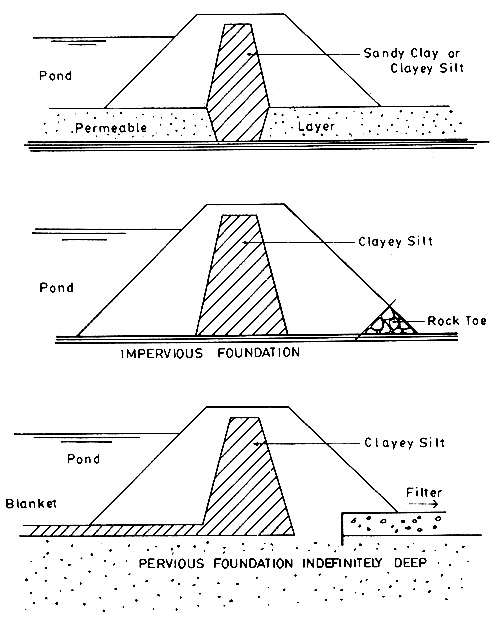
Figure 1. Examples of dike with core walls
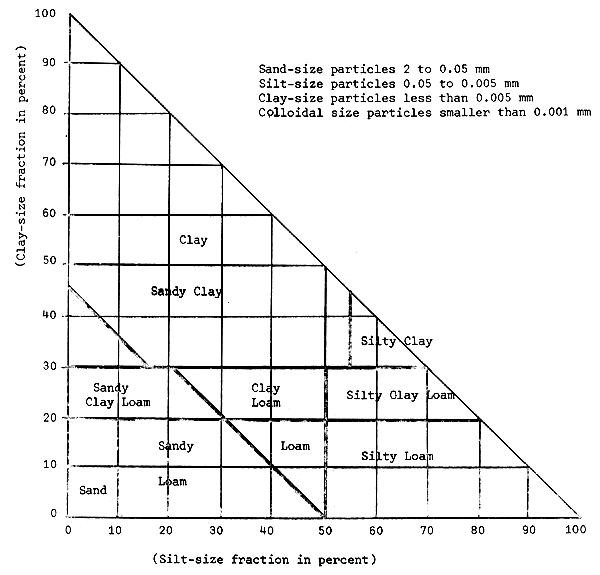
| Example: | A soil contains | 28 percent clay |
| 45 percent silt | ||
| 27 percent sand (by difference) |
This is located as point A in above figure and its classification is found to be “clay loam”. The above textural chart gives the grainsize distribution and hives it a textural name and does not reveal the other physical characteristics.
Figure 2. Textural classification chart for soils U.S. Bureau of Public Roads
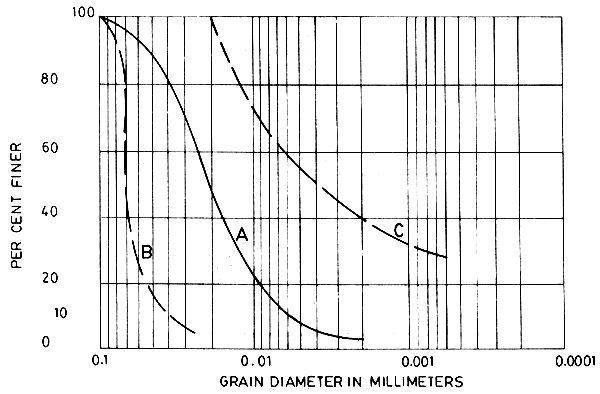
Figure 3. Grain size distribution curves
Soil A - Well graded, having all sizes of grains in such a proportion that makes it easy to compact to maximum density
Soil B - Coarse fraction predominant
Soil C - Fine fraction predominant
| Uniformity coefficient, C | 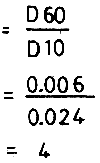 |
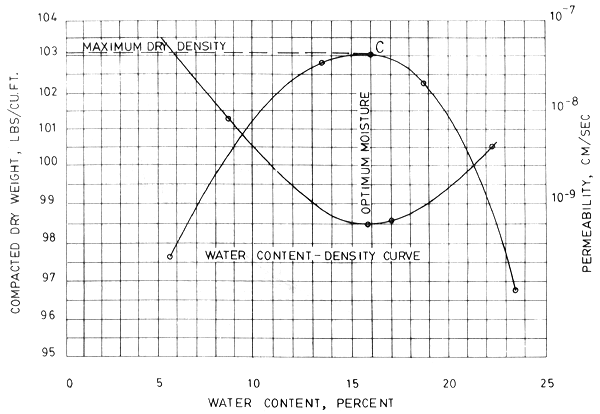
Figure 4. Water content density & water content permeability relationships
The peak of the curve represents the maximum density (at maximum compaction) for a given soil for a given compactive effort and the percentage of water content at this point, C, is known as the “optimum” water content, the moisture content necessary to give maximum compaction and minimum permeability (AASHO) Standard Procedure T-99
Maximum Dry Density - 103.3 lbs/cu ft. (1660 kg/cu m)
Optimum Moisture Content - 16.0%

Figure 5. Relationship between stability factor Ns, slope angle θ, & depth factor Nd, for a purely cohesive (Æ=0) soil. (after D.W. Taylor)
| (A) | Rotational slip at toe (Toe failure) |
| (B) | Rotational slip at front of slope base |
| (C) | Slope failure “circle on slope” |
SCSP-SFDC/77/AEn/CP35
by
J.R. Lopez
Development Bank of the Philippines
Iloilo Branch, Iloilo City
Philippines
(Summary)
Some 173 000 hectares of privately-owned and leased aquaculture projects in the Philippines produced 104 000 metric tons of fish in 1975. Extensive areas of swamplands remained untapped. While present yield is said to be 600 kg/ha, there is sufficient evidence to prove that productivity of established and new aquaculture projects can be raised significantly.
Cost of development, or modification of aquaculture projects, is considered high in the light of experiences with the use of machinery in pond construction. Employment of skilled manual labour, which is abundant in most areas, is still preferred as a measure to provide income to the work force in the community.
Funding assistance comes from the development banks, the commercial and savings banks and the rural banks. Among the members of the banking community, the Development Bank of the Philippines (DBP) assumes a leading role in extending credit for aquaculture development.
Because of their conservatism, most banks lend funds against the security of collaterals, especially real estate properties. However, as early as 1952, the DBP shifted to lending on the basis of project viability and debt-servicing capacity. The DBP's financing programme for aquaculture development was liberalized in several stages in order to make the scheme responsive to the needs of the fisheries industry.
Characteristics of the site and the selected pond system design influence the investment plan for the development of an aquaculture project. A proposed investment plan when presented to a funding agency, particularly the DBP, is evaluated in terms of viability and debtservicing capacity. Drawdown of bank funds is programmed to match the funding requirement of project development.