Models developed in Chapters 2 and 5 satisfy the dynamic pool assumption and thus homogeneity in the spatial distribution of the stock and fishing effort exerted (e.g. pelagic species). In sedentary resources (e.g., mollusks), the above assumption is not always valid for the following reasons (see Hancock, 1973; Caddy, 1975; Orensanz & Jamieson, 1998):
Populations are patchily distributed (Elliot, 1977).
The low or null mobility precludes species redistribution over a fishing ground, by filling gaps in patches resulting from a sequential distribution pattern produced by the heterogeneous allocation of fishing effort (Hancock, 1979; Caddy, 1989a, b; Conan, 1984; Orensanz et al., 1991). Thus, CPUE cannot be used as an unbiased index of abundance.
Growth, mortality and recruitment parameters are extremely dependent on environmental conditions even between small distances (Orensanz, 1986; Defeo, 1993a).
Two alternative approaches seem to be appropriate:
To relax the assumption of spatial homogeneity of stock distribution. Thus, extensive fishing grounds with variability in environmental conditions and related abundance heterogeneity, growth and mortality patterns, can be divided into smaller areas that can be considered as independent units (Caddy, 1975; 1989a; b; Hall, 1983; Sluczanowski, 1984; 1986). Hence, for a stock showing a continuous geographic range of population characteristics, a useful approach is to consider it as composed of several discrete subpopulations which can be studied independently, and the predictions integrated afterwards (Seijo et al., 1994b, c).
To develop a comprehensive approach, integrating effects of different environmental regimes on the spatial structure of the population, spatial heterogeneity of fishing effort, biological interactions, and the implications of economic factors and human attitudes (behavior of resource managers and users) (Seijo & Defeo, 1994a; Seijo et al., 1994c). In view of the uncertainty involved in the above factors (Lewis, 1982; Anderson, 1984; Sissenwine, 1984a, b; Seijo, 1987), it is preferable to build stochastic models instead of deterministic ones, in which point predictions are replaced by probability functions (Botsford, 1986; Seijo, 1986; Fogarty, 1989; Seijo & Defeo, 1994a; Seijo et al., 1994b).
Studies on fishing effort dynamics have been focused on long-term decisions of fishers, emphasizing the estimation of rates of entry and exit to the fishery and the characterization of general patterns of allocation of fishing intensity (Smith, 1969; Clark, 1976; Mangel & Clark, 1983; Emerson & Anderson, 1989). However, it is in the short-term that fishers make their spatial decisions: after deciding to go fishing and selecting the target species they decide where to fish (Hilborn & Ledbetter, 1979; Bockstael & Opaluch, 1983; Defeo et al., 1991; Eales & Wilen, 1986). The latter decisions are of utmost importance, because, in contrast with traditional views which focus on excess of fleet capitalization, dissipation of economic rent can arise primarily as a result of today's excess of fishermen's movements in response to yesterday's spatial catch rate variations.
In this Chapter, spatial considerations in modelling fisheries are introduced, notably the distance from ports to fishing grounds, in order to further understand short-run decision-making of fishers in their allocation of fishing intensity. We also add a degree of complexity in the interdependencies discussed in Chapter 3, incorporating the spatial dimension in the analysis, with special reference to fisheries where the dynamic pool assumption is not satisfied.
Modelling the spatial dynamics of fisheries in the short-term allows us to better understand the intertemporal allocation behavior of fishing effort and thus to develop adequate management strategies. Some strategies of spatial allocation of effort have been indentified:
Proportional allocation according to the spatial abundance of the resource (Caddy, 1975).
Sequential allocation to those patches of greatest abundance (Hilborn & Walters, 1987).
Random search (Hilborn & Walters, 1987).
Free distribution of allocation of fishing intensity (Gillis et al., 1993).
Proportional allocation to (Defeo et al., 1991; Seijo et al., 1994b):
The quasi rent of variable costs (including transfer costs resulting from moving from port to alternative fishing grounds).
The friction of distance, i.e., non-monetary costs associated to distance.
The probability of finding the target species at profitable levels.
With the above considerations in mind, we present two models developed by Seijo et al. (1994b), with different degree of complexity in spatial resolution and requirement of bioeconomic information.
ALLOC is a short-run bioeconomic model that represents interdependencies between two fleet types (e.g. artisanal and mechanized/industrial) coming from different ports of origin that capture the same target species in alternative fishing grounds (Seijo et al., 1994b).
Spatial and temporal dimensions are incorporated in this discrete dynamic model by specifying: (1) CPUE's by fishing grounds; (2) distances from ports to different fishing grounds; and (3) a function that determines the short-run spatial allocation of fishing intensity. The latter is modelled in ALLOC as a function of the distances from ports to alternative fishing grounds, the net revenues perceived in the previous trips, and the probability of finding the target species in each ground at profitable levels.
The spatial dynamic allocation of fishing intensity (i.e., effective effort per unit of area, sensu Gulland, 1983: 44) of vessels type m from port h among fishing grounds k in time t(fkhm(t)) is given by:
fkhm(t)=SAEkhm(t)DAYS·Vhm(t) (6.1)
where SAEkhm(t) is a (0,1) optimum spatial distribution of fishing vessels; DAYS is the average number of effective fishing days per month; and Vhm(t) is the number of vessels type m of port h which seasonally allocate their fishing effort to the target species. SAEipm(t) is estimated by:
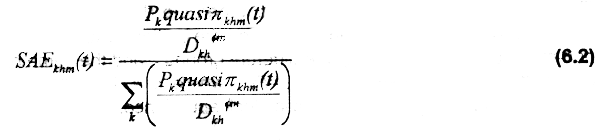
where Pk is the probability of finding the target species at profitable levels in alternative fishing grounds k, quasiπkhm(t) is the quasi rent of variable costs received by the average vessel type m from port h in ground k in time t, Dkh is the distance to fishing ground k from port h; and φm is a weighing factor called friction of distance for vessel type m. Pk can be estimated by the ratio between total fishing trips per ground and the number of trips where the target species was found at profitable levels, i.e., for those CPUE that generated net revenues greater than or equal to variable costs of fishing effort.
Additional to the transfer costs from the port of origin to alternative fishing grounds, one element considered in this model as a key explanatory factor for the spatial behavior of fleets is the friction of distance (Isard & Liossatos, 1979, Seijo et al., 1994b). Artisanal boats with limited autonomy are assumed to give substantial weight to non monetary costs derived from e.g., insecurity associated with fishing far away from port, as well as other environmental and cultural factors that assign non-monetary costs to distance. Thus, ALLOC implicitly incorporates in Dkhφm all those non-monetary factors associated with distance. The weight of this parameter for a specific fleet type m, is given by the power to which distance is raised (Dkhφm in equation 6.2).
To observe the short-term fleet performance, an estimation of the quasi rent received by an average vessel type m from port h is needed:
quasiπkhm(t) = TRkhm(t) - VCkhm(t) (6.3)
where TRkhm(t) are the daily total revenues received by vessel type m from port h by harvesting in fishing ground k in time t, and VCkhm(t) are the variable costs of fishing effort incurred by vessel type m by fishing one day in ground k in time t.
VCkhm(t) are estimated considering: (a) transfer cost (as a function of distance) defined as the product of Dkh and the average cost of oil and gas per km traveled (θ); and (b) the value of the proportion of the catch (ω) assigned to the crew as labor payment. Other variable costs (e.g., bait, gear maintenance and repair) are pooled together in a parameter called OVCm:
VCkhm(t) = ωqmBk(t) + θDkh + OVCm (6.4)
In the short-run, vessels will remain in the fishery if TRkhm(t)≥ VCkhm(t), i.e., the quasi rent of variable costs ≥ 0. Considering the SAEkhm(t) function, at least four types of distributions that account for spatial variations in fishing intensity can be described (Table 6.1):
Case 1: artisanal littoral fisheries. When the distance is irrelevant in terms of transfer costs from port to alternative grounds (θ=0) and the friction of distance is zero (φ=0), i.e., there are not non-monetary costs to fishing the different grounds, and the same probability of finding the species at profitable levels exists (P1=P2=…=Pk, where k = 1…n), the resulting SAEkhm(t) distribution is proportional to the spatial variations in stock abundance.
Case 2: fisheries in protected coastal zones. Where transfer distances to alternative grounds from port are relevant (θ>0), but non-monetary costs are negligible because of the easy operation and navigability in protected fishing grounds (φ=0), and there is the same probability of finding the species at profitable levels (P1=P2=…=Pi, where i = 1…n), the SAEkhm(t) distribution is then proportional to spatial variations in the quasi-rent of variable costs.
Case 3: fisheries in exposed coastal zones. When θ>0, the friction of distance is substantial (φ=0), and P1=P2=…=Pk, the SAEkhm(t) distribution is proportional to the spatial distribution of the quasi rent and inversely related to the friction of distance from port to the alternative grounds.
Case 4: fisheries with high information costs. When transfer distances from port to alternative grounds are relevant in monetary terms (D>0 y θ>0), friction of distance (φ>0) occurs, and there is heterogeneous probability of finding the resource at profitable levels (P1# P2#…# Pk), the distribution of SAEkhm(t) is proportional to the spatial distribution of the quasi rent and to the probability of finding the resource at profitable levels, and inversely related to the friction of distance from port to alternative fishing grounds.
| CASES | Monetary cost of distance D | Friction of distance (φ) | Probability of finding the resource (P) | Expected distribution |
|---|---|---|---|---|
| Case 1 | D1=D2=…=Dk θ=0 | φ=0 | P1=P2=…=Pk | Proportional to the abundance |
| Case 2 | D1∞D2…Dk θ>0 | φ=0 | P1=P2=…=Pk | Proportional to the quasi rent |
| Case 3 | D1∞D2…Dk θ>0 | θ>0 | φ=0 | P1=P2=…=Pk Proportional to the quasi rent and 1/Dφ |
| Case 4 | D1∞D2…Dk θ>0 | φ=0 | P1∞=P2∞=…=Pk | Proportional to the quasi rent, 1/Dφ and Pk |
The cumulative economic rent received by vessel type m from port h over the fishing season is estimated by:
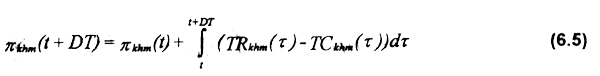
where TRkhm(t) are the total revenues received by vessel type m from port p by harvesting in fishing ground k, in time t; and TCkhm(t) are the total costs of fishing effort incurred by the fleet type m by fishing in ground k in time t.
TRkhm(t) and TCkhm(t) are estimated respectively as:
TRkhm(t) = (qmBk)(t)Ptar + Cine Pinc) f khm(t) (6.6)
TCkhm(t) = FCmVhm + VC khm(t) f khm(t) (6.7)
where: Ptar and Pinc are, respectively, the average price paid per kg of target and incidental species; Cinc is the average incidental catch per fishing trip of vessel m; qm is the catchability coefficient of vessel type m; Bk(t) is the biomass of the target species in fishing ground k in time t; FCm is the daily fixed cost for vessel type m; and Vhm is the number of vessels m from port h. Fixed costs include interest payments from borrowed capital to buy a boat, engine and gear, their depreciation, administration and insurance costs, and the opportunity cost of capital.
The dynamic catch rate is estimated as:
Ykhm(t)=(qmBk(t) + RVkhm(t)) f khm(t) (6.8)
where the random variable RVkhm(t) is generated with an exponentially autocorrelated probability density function, using the observed variance of daily catch for vessels type m when fishing in ground k. This variable accounts for catch variability not explained by variations in q, B and f in each fishing ground. It is exponentially autocorrelated to represent the fact that random catch variations at one day are not independent of previous values: (a) today's catch is dependent to a certain extent of yesterday's catch; (b) selection of fishing ground is partially dependent on previously selected grounds; (c) environmental factors affecting resource abundance tend also to be dependent on previous values. This variable is generated by subroutine EXACOR (Manetsch, 1986), which uses an uniformly distributed random variable between 0 and1, that is further transformed to the selected probability density function. Other probability density functions can be used to generate random variables, by employing the inverse transformation method or even numerical methods, depending on whether the probability density function can be integrated analytically to obtain the cumulative distribution function or not (Gottfried, 1984).
The catch per unit of effort of vessel type m in ground k in time t (CPUEkm(t)) is estimated by:
CPUEkm(t)=qmBk(t) (6.9)
Biomass for each fishing ground Bk(t) is estimated by spatially disaggregating the logistic function:
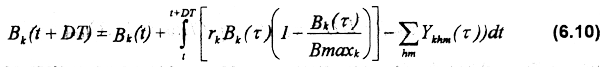
where rk and Bmax, are respectively, the intrinsic growth rate and the maximum biomass in ground k.
A time lag frequency distribution representing the rate at which small-scale fishing fleets enter the seasonal fishery or shift from one fishery to another, is frequently observed (Seijo et al., 1987). Hence, time lags in the short-run dynamics of fishing fleets are incorporated in ALLOC to relax the assumption that every boat that eventually will fish for the seasonal target species, will enter the fishery exactly the first day of the season. This aspect is incorporated through the distributed DELAY model (Manetsch, 1976) based on the Erlang (Gamma) probability density function (Seijo, 1987). Thus, the seasonal dynamics of vessel type m from different ports (Vhm(t)) can be described by a distributed delay function of order g by the following set of differential equations (see also Chapters 2 and 4):
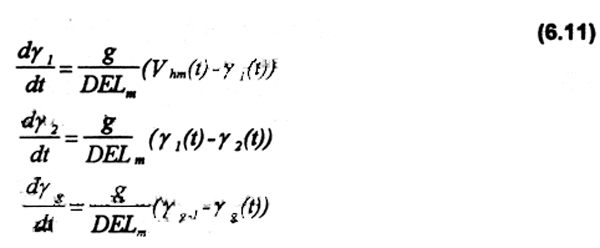
where Vhm is the input to the delay process (number of vessels from port h which will allocate their fishing effort to target species); γtg(t) is the output of the delay process (number of small-scale boats enterning the fishery along the season); γ1(t), γ2(t),…, γg-1(t) are intermediate rates of the delay; DEL is the expected time of entry of vessels to the fishery; and g is the order of the delay. The parameter g specifies the member of the Gamma family of probability density functions.
The cumulative spatial allocation of fishing intensity along the fishing season of fleets m from port h in ground k (fakhm(t)) is given by:
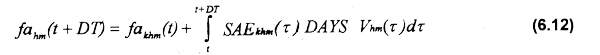
The spatial allocation of fishing intensity among alternative fishing grounds is a function of the probability of finding the target species, the net revenues obtained from different fishing grounds in previous trips, and the distances to alternative fishing grounds from different ports of origin.
CPUE is a function of q and the resource biomass in each fishing ground over time, and will tend to decrease as fishing intensity and the corresponding exploitation rate (sensu Gulland, 1983) increase at ahigher rate than the natural biomass growth rate in each site.
There is no cross migration or immigration among fishing grounds.
Uncertainty in the spatial allocation of fishing effort over time is represented by random variables (0, VAR) with an exponentially autocorrelated probability density function.
Fishers price-taking behavior (Clark, 1985) was assumed for prices of target species and incidental catch. This assumption could be relaxed if a robust time series of fish price, quantity harvested and real income of resource consumers were available.
Costs of inputs needed per fishing trip remains constant along the fishing season.
When bioeconomic information is available, some of the assumptions made in ALLOC can be relaxed to achieve a better representation of the population dynamics and of the spatial resolution of the model. CHART is an age structured, dynamic spatial model that incorporates the main features of the YRAREA model (Caddy, 1975) with the short and long run dynamics of the fishing fleets in a bioeconomic and geographic context (Seijo et al., 1994b).
The initial population structure is estimated by the maximum observed CPUE on each ground (CPUEmaxkl), where k is the latitude and / the longitude. Maximum biomass in each geographic cell kl(Bmaxkl) is obtained by dividing CPUEmaxkl by an average q per unit area. Recruitment over time can be specified as constant, dynamic, deterministic or stochastic. It involves a general stock-recruitment function built-in in addition to the upper bound imposed by the estimated maximum biomass of each cell of the geographic area. The model uses a Beverton-Holt stock-recruitment type of model (Beverton & Holt, 1957). For a given maximum recruitment (Rmax), the number of recruits is estimated as follows:
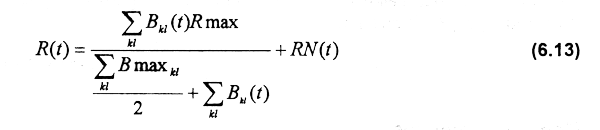
where Bkl(t) is the biomass in cell kl; and RN(t) is a (0, var) normally distributed random variable.
Total number of recruits for each year is seasonally distributed through the use of a distributed delay function, which specifies the peak recruitment month and its period (in months) of occurrence. The spatial distribution of recruitment patches is generated by randomly selecting the recruitment patch center coordinates, and then calculating recruitment density out from patch center by using the bivariate normal distribution (Caddy, 1975):

where: Rkl(t) is the number of recruits located in the patch center of the cell kl in time t; NT(t) is the number of recruits to be distributed within each patch before biomass constraint (see Seijo et al., 1994b); σ is the standard deviation of the patch density (0 < σ < 1), and x is the distance of unit area kl from patch center, estimated by:
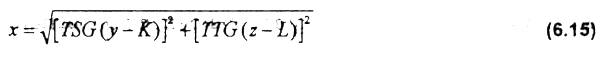
where TSG and TTG are, respectively, the length and width of the cell, estimated by a previously specified spatial resolution (e.g. degrees, minutes and seconds). Moreover:
| i = 1, 2, 3,…, SG | and | SG = number of rows in the geographic grid. |
| j = 1, 2, 3,…, TG | and | TG = number of columns in the geographic grid. |
| y = SG/2 | and | z = TG/2. |
The biomass allocated in each cell kl is estimated by:

where Njkl(t) is the number of individuals at age j in site kl in time t and mage is the maximum observed age. Average individual weight at age (Wj) is calculated by the von Bertalanffy growth equation and the corresponding length-weight relationship:
Lj = :∞(1 - e(-kp(j-to))) (6.17)
Wi = aLbj (6.18)
where a and b are constants.
The spatio-temporal distribution of population structure (Njkl(t)) is estimated by:
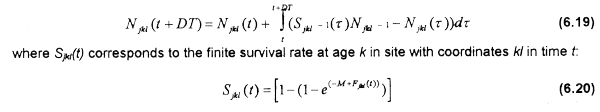
where M is the instantaneous natural mortality rate and Fjkl(t) is the age specific fishing mortality rate in site kl in time t, estimated by the product of the age-specific qj by the intensity of fishing exerted in site kl in time t (fkl(t)).
CPUE in site kl in time t (CPUEkl(t)) is estimated by:
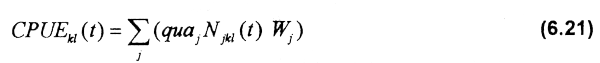
where the age specific catchability per unit of area (quaj) is estimated using the area swept equation of Baranov (1918) and the logistic selectivity curve (Sparre et al., 1989):

where: pcap is the probability of capture by the gear; area is the area swept per day; SELj is the age-specific gear retention (see Chapter 4); and AREA is the area occupied by the stock.
Short-run spatial allocation of fishing intensity (e.g. within the fishing season) is estimated as in ALLOC, with one modification: parameter Pk is substituted by the perceived risk of fishing on the fishing ground with coordinates kl.
Spatial allocation of fishing intensity of vessels from port h in site kl in time t, (fklh(t)) is given by:
fklh(t) = SAEkhm(t)DAYS Vh(t) (6.23)
where: Vp(t) is the number of vessels from port h that seasonally allocate their fishing effort to the target species; and SAEklh(t) is a (0,1) distribution of vessels of port h into sites with coordinates kl, in time t, which can be estimated as:

where Riskkl is the perceived risk of fishing in alternative grounds kl. This parameter is specified in the model with a range of values [1–3], where 1 implies absence of risk and 2–3 indicates increasing risk levels. Catch and economic rent for each ground are estimated as in ALLOC.
The number of boats from port h present in the fishery over time (years), is modelled by spatially applying Smith (1969) equation:

where is a positive constant. Equation (6.25) states that in the long-run and under open access conditions, if the sum of net revenues obtained from all fishing grounds is: (i) positive, there will be entry to the fishery; (ii) negative, exit is expected to occur; and (iii) zero, the fishery is at bioeconomic equilibrium, and there will be no stimulus for exit/entry.
Recruitment does not occur at a single point in time, but within a period whose distribution is modelled by the distributed delay model.
Extension of patches is defined by the density variance of a bivariate normal distribution.
Migration, dispersal and movement are not considered.
Natural mortality is constant for all ages.
Spatial allocation of fishing intensity is a function of ground-specific variations in the: (a) quasi-rent, (b) risk of fishing, and (c) distances from different ports.
Distances between ports and fishing grounds are estimated geographically without consideration of possible obstacles.
For the long-term fleet dynamics, an estimated time lag of 6 months is assumed for vessel entry/exit to the fishery, whereas in the short-run, the user is requested to provide the observed average time lag of entering the seasonal fishery.
Uncertainty of daily catches in each ground is modelled by an exponentially autocorrelated probability density function.
Price of target species and costs of fishing effort inputs are constant and exogenously determined.
The interested reader can conduct simulation experiments with these spatial models, which are contained in the package SPATIAL published by FAO (Seijo et al., 1994b).
Seijo & Defeo (1994a) conducted a short and long run analysis of the yellow clam Mesodesma mactroides fishery of Uruguay. For this end, a dynamic, non-linear and stochastic model was built to represent the behavior of resource and fishers through time. The short term space-time distribution of fishing effort was represented as a function of the dynamic catch per unit effort in 4 alternative grounds, the distance from different localities, the perceived probability of finding the species at profitable levels, and the corresponding net revenues obtained in the previous fishing trip (see also Defeo et al., 1991). The long-term dynamics of the fishery considered time lags in spawning, hatching and recruitment processes, as well as in fishermen's entry and exit to the fishery. The distributed delay model was applied for this purpose. A stock-dependent, overcompensatory (Ricker) function characterized the dynamics of the stock-recruitment relationship (Defeo, 1993a). Recruitment was modelled by using the distributed delay model (gamma function of order 3) in accordance with a recruitment period of 4 months. A dynamic and density-dependent natural mortality was estimated as a function of the initial density of recruits and salinity (which is substantially affected by the outflow of freshwater creeks) on each fishing ground. Effort dynamics in the long-run (number of fishers from locality h present in the fishery over time) was modelled by spatially applying the Smith (1969) equation and the distributed delay model (see Seijo & Defeo, 1994b). Price of species, opportunity costs of labor and operation costs were also included in the model.
Simulation experiments were conducted with three management strategies to observe the dynamic impact on performance variables. The following three policy vectors were simulated and compared with the base run representing the current management scheme (minimum size restriction of 50 mm, and 50 fishing licenses):
The current management scheme and a catch quota of 50 tonnes/year.
A minimum harvestable size of 43mm (size at sexual maturity) and 150 fishing licenses.
Minimum size restriction of 50–mm and 150 fishing licenses.
The model reproduced well the temporal variability in abundance of recruits (Fig. 6.1a) and adults (Fig. 6.1b), and was statistically validated. Adults markedly increased from 1988 on, as a result of a human exclusion experiment conducted between March 1987 and November 1989 (see Defeo, 1993a; 1996, 1998; Defeo & de Alava, 1995 for details). Recruitment was inhibited in 1989 and 1990, as a result of overcompensation due to high adult densities. This fact has important management connotations: simulation showed that, as a result of a prolonged closed season (more than 2 years), high adult density could inhibit recruitment success and hence the magnitude of the stock available for fishing two years later (see Fig. 6.2).
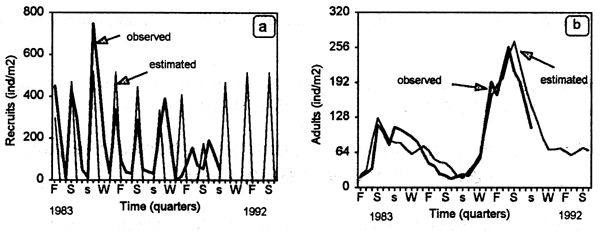
Figure 6.1 Mesodesma mactroides. Observed vs. estimated densities of (a) recruits and (b) adults.
The fishery showed a strong seasonal component. The model (Fig. 6.2) adequately reproduced the marked increase in catch and fishing intensity during summer and spring. A decline in the demand for local market consumption and a reduced availability of the resource because of downward migration towards the infralittoral explained the diminished catches in autumn and winter (Defeo, 1989). The model also satisfactorily explained the marked spatial variability in effective fishing days, catches and fishing intensity (Fig. 6.3a; see also Defeo et al., 1991), as well as spatial variations in the economic rent. Fishermen spatially allocated fishing effort proportionally to spatial variations in stock abundance, i.e., the central zones 2 and 3, with greater stock abundance presented highest yield values (Fig. 6.3b) and fishing intensity. The model correctly represented variations within and between years. As a result of the above mentioned trends and the marked seasonality of the fishery, net revenues were also greater from the central grounds, peaking in spring and summer (see also Defeo et al., 1991 for a detailed analysis).
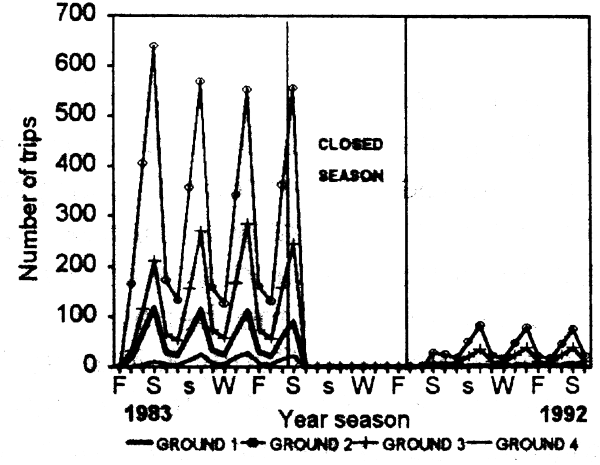
Figure 6.2 Seasonal variations in simulated fishing intensity by fishing ground from 1983 to 1992 for the yellow clam fishery of Uruguay.
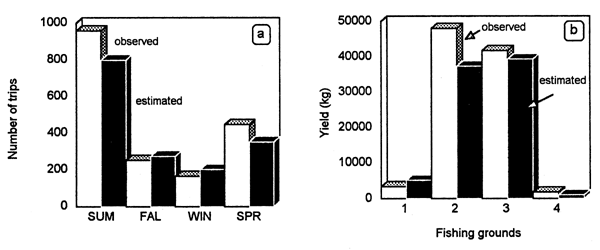
Figure 6.3 Mesodesma mactroides. Comparison of observed vs. simulated: (a) seasonal fishing effort; and (b) catches by fishing ground (summer 1985).
According to the results obtained, a spatial management scheme based upon a rotation of areas was proposed, taking into account periods of unequal demand for the product and temporal variations in stock accessibility and abundance. Because of relatively low total costs, the bioeconomic equilibrium is estimated at high levels of fishing effort, which in turn increases the risks of exhausting this highly vulnerable sedentary species.