Abstract: Excess capacity is globally recognized by resource managers as a major problem for fisheries. Yet, the concept of capacity remains vague, ill-defined, and often ambiguous. Presently, measuring capacity and capacity utilization in fisheries has become more important or of greater public concern than ever because of various national and international agreements or policies to reduce capacity in fisheries throughout the world. In this study, we propose data envelopment analysis (DEA) as one method that may be used to calculate a production-oriented measure of capacity. We conclude that although the DEA approach is limited and does not provide measures of capacity and CU consistent with the long-run optimum scale of operation, it can provide information useful to resource managers concerned with downsizing fleets or matching capacity to resource levels. We illustrate the approach by examining the capacity of ten sea scallop vessels operating between 1987 and 1990. We conclude that the ten vessels had the capability to harvest considerably more than they actually did, and the fleet should be reduced by 68 percent or more if managers desire to match capacity to a recommended sustainable yield of 20 million pounds.
The potential for excess capacity has been a long-standing argument to support access controls in fisheries. Simply, in the absence of access controls, firms enter a fishery until it is no longer profitable for other entities to enter. Although this outcome is no different than the long-run competitive equilibrium at which profit is also zero, it is troublesome because of the possibility of technological externalities, excessive harvesting capability, and the potential for economic waste. That is, the resource at any time is finite, and entry can lead to a fleet that is capable of harvesting well in excess of any reasonable sustainable level. Alternatively, production is neither technically efficient nor at minimum cost (i.e. there is economic waste because more resources are used to harvest a given level of output than is actually necessary).
Most recently, Mace (1997), before a World Congress meeting on sustainable fisheries, stated that excess harvesting capacity was the most important problem confronting fishery managers. Representatives from approximately 40 nations, in fact, recognized that excess capacity was such a serious problem that an international study should be undertaken to define and develop measures of capacity and capacity utilization (CU). This international study was sponsored and managed under the auspices of the Food and Agriculture Organization (FAO) and was to be conducted in two phases: (1) development and international acceptance of the definitions of capacity and capacity utilization, and (2) the development and acceptance of methods to assess or calculate capacity and CU.
A major reason for the concern is that many nations need to reduce capacity in order to comply with various national and international fishery agreements (e.g. Code of Conduct for Responsible Fisheries). The need to understand and measure capacity is equally important to the United States. The Sustainable Fishing Act of 1996 requires that resources be rebuilt to at least maximum sustainable yield (MSY) levels within a ten-year period (United States Congress, 1996). Under the present United States regulatory regime, the only permissible option for rebuilding many fish stocks is a drastic reduction in fishing activity.
There are three broad options available to United States regulators to reduce fishing activity. One, regulators may impose extremely stringent regulations on fishermen which could even include a moratorium on harvesting activities; the necessary levels of reduction in fishing activity for most fisheries, however, will impose extreme financial hardship and possibly bankruptcy for many vessel owners. Second, regulators may implement either a public or private funded buyback programme to purchase active vessels and reduce capacity. Third, regulators could subsidize the present vessel owners until stocks did rebuild; this last option is not one that has even been considered by regulators or the United States Congress. A fourth option is rights-based strategies such as individual transferable quotas (ITQs); ITQs or similar rights-based strategies (e.g. individual transferable effort programmes), however, are prohibited under the present regulatory regime. It appears that the only viable short-term option is some type of capacity reduction programme such as a vessel buyback. If a buyback programme is to be implemented with the intent of matching harvesting capacity to resource levels, managers must have information about capacity and capacity utilization.
Although there is widespread recognition that capacity in fisheries must be reduced, the term, capacity, remains vague and generally ill-defined when considered for the case of fisheries. The vagueness exists despite a long and rich history of research on capacity in conventional industries and fisheries by economists (e.g. Klein and Summers, 1966; Morrison, 1985a, 1985b and 1986; Berndt and Fuss, 1989; Nelson, 1989; Apostle et al., 1993; Christy, 1996; Augstyn, 1996; Banks, 1997; Valatin [no date])[143]. Between 1996 and 1998, the Food and Agriculture Organization and various nations attempted to define and develop measures of capacity and capacity utilization for fisheries.
In nearly all the FAO-sponsored studies, however, researchers actually attempted to define and develop measures of capital and capital utilization. In a limited number of cases, though, researchers did attempt to develop standardized measures of capacity based on various vessel characteristics and potential catch. The purpose of developing these standardized measures was to facilitate downsizing various fleets in accordance with removing or reducing harvesting capacity (e.g. a 50 gross registered ton vessel constructed of steel and having 400 horsepower equated to a potential harvest of 75 metric tonnes a year).
There are many definitions of capacity. Johansen (1968: p. 52), though, provides a widely accepted and useful definition "...the maximum amount that can be produced per unit of time with existing plant and equipment, provided the availability of variable factors of production is not restricted." The Johansen definition is a short-run concept of capacity in that there are fixed and variable inputs. Johansen's definition is, nevertheless, equivalent to the FAO general definition of capacity agreed upon by researchers representing forty nations at a Technical Working Group meeting held at La Jolla, California in April 1998. Alternatively, the FAO definition states that capacity output is the maximum output that could be produced given full and efficient utilization of the variable and fixed factors of production. The Johansen and FAO definitions are also equivalent to the definition offered by Christy (1996): The capacity of an individual fishing unit is a measure of the quantity of fish that it can take, assuming there are no limits on the yield from the stock, or stocks. Fleet capacity is the sum of the capacities of all fishing units in the fishery. Presently, a United States Congressional Task Force on capacity and subsidies in fisheries is using a nearly identical definition to that provided by Johansen, FAO, and Christy.
The Christy (1996), FAO (1998), United States Congressional Task Force, and Johansen (1968) definitions are all primal based in that they do not directly assess capacity from a cost or economic framework. The definitions may be viewed as technological-engineering definitions (Kirkley and Squires, 1999). In contrast to the primal-based definition, Morrison (1985a, 1985b, 1986), Nelson (1989), and Berndt and Fuss (1989) offer an economic based definition of capacity. The economic concept of capacity is defined as the output level coinciding with an equilibrium between the minimum long-run and short-run average cost curves. Berndt and Fuss (1989), however, have shown that there may be an indeterminancy problem when there are multiple products and more than one fixed or quasi-fixed factor of production. Thus, empirical implementation of the economic definition often requires aggregation over outputs and multiple fixed factors. More recently, Färe and Grosskopf (1998) offered an approach that may avoid the indeterminancy problem by using a dual data envelopment approach to measure or assess capacity.
While the approaches of Färe and Grosskopf (1998), Morrison (1986), Berndt and Fuss (1989), and Nelson (1989) are all useful and capable of providing important information, they are not likely to be very useful for assessing capacity in fisheries. Simply, the data necessary for such measures are typically unavailable for fisheries. Moreover, resource managers appear to be more interested in a primal based approach; an approach which is more consistent with the types of data typically available on fisheries and the requirements of various national and international policies (e.g. the Sustainable Fishing Act of the United States). If any type of guidance for capacity reduction programmes is to be provided to resource managers, it is a likely that such guidance will have to be based on a primal approach.
Given the widespread recognition that excess capacity is a major problem for fisheries, it is quite alarming that there has been little work to develop or adopt existing empirical methods to determine capacity, capacity utilization, and input utilization in fisheries. Two approaches which may be used are the peak-to-peak approach of Klein and Summers (1966) and the DEA approach of Färe (1984), Färe et al. (1989), and Färe et al. (1994). Both approaches, however, restrict capacity measures to the short to intermediate time period (i.e. only variable inputs may be changed). The peak-to-peak approach was used by Ballard and Roberts (1977) to examine capacity utilization rates of fishing vessels in ten major Pacific coast fisheries. The peak-to-peak approach, although having widespread applicability in the examination of capacity in United States industries, fails to offer guidance on technical efficiency and optimum input usage. In contrast, the DEA approach of Färe et al. (1989) explicitly eliminates any bias caused by failing to adjust the capacity and capacity utilization rates for inefficiency (i.e. CU with respect to the frontier).
The Färe et al. (1989) approach is based on solving an output-oriented linear programming (LP) problem. The solution to the LP problem of Färe et al. (1989) provides measures of technical efficiency corresponding to capacity output. The Färe et al. approach also can be used to obtain information about optimum input usage or input utilization rates. In addition, the Färe et al. (1989) or DEA approach easily accommodates multiple products and multiple fixed factors; this is not the case for the conventional economic-based assessment methods.
A third possible approach is the one-stage stochastic frontier approach of Battese and Coelli (1995). With appropriate modification of Battese and Coelli's (1995) approach, it may be possible to determine the maximum output corresponding to technically efficient production and conditional on the most binding fixed factor of production. We do not further consider the stochastic frontier approach of Battese and Coelli (1995), however, because the necessary procedures have not been formally developed and the approach cannot accommodate multiple outputs, which are common in fisheries.
In this paper, we provide a review of the DEA approach of Färe et al. (1989) and Färe et al. (1994). Using a panel data set on ten scallop vessels operating between 1987 and 1990, we examine capacity, capacity utilization, and input utilization. We determine that the sample fleet had considerable excess capacity relative to what they harvested. Alternatively, the fleet had the capability to harvest considerably more scallops than it actually did. We also suggest that the fleet operated at levels that were sub-optimal relative to full capacity. That is, the number of days at sea and crew size per trip was sub-optimal. Last, we show that for trips with high resource abundance, the fixed factors rather than the resource abundance actually limited production.
Following Färe et al. (1989), let there be j
= 1,...,J observations or firms in an industry producing a scalar
output ujÎR+
by using a vector of inputs
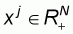 We also assume that for each
n
We also assume that for each
n 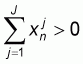 , and for each
j,
, and for each
j, 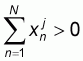 .The first
assumption states that each input is used by some firm. The second assumption
indicates that each firms uses some input. A remaining assumption is that each
firm produces some output, uj > 0 for all
j.
.The first
assumption states that each input is used by some firm. The second assumption
indicates that each firms uses some input. A remaining assumption is that each
firm produces some output, uj > 0 for all
j.
In order to calculate Johansen's notion of capacity, Färe et al. (1989, 1994) propose the following data envelopment analysis (DEA) problem:
|
maxqlz q |
|
|
s.t.
|
|
|
|
(1) |
|
|
|
|
|
|
The variable factors are denoted by
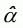 and the fixed factors are
denoted by
and the fixed factors are
denoted by  . Problem (1)
enables full utilization of the variable inputs and constrains output with the
fixed factors. Moreover, l is a measure of the
ratio of the optimal use of the variable inputs (Färe et al., 1989,
1994). Problem (1) imposes constant returns to scale, but it is a simple matter
to impose variable returns to scale (i.e. variable returns to scale requires the
constraint
. Problem (1)
enables full utilization of the variable inputs and constrains output with the
fixed factors. Moreover, l is a measure of the
ratio of the optimal use of the variable inputs (Färe et al., 1989,
1994). Problem (1) imposes constant returns to scale, but it is a simple matter
to impose variable returns to scale (i.e. variable returns to scale requires the
constraint 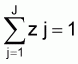
The parameter q is the reciprocal of an output distance function and is a measure of technical efficiency relative to capacity production, q £ 1.0. It provides a measure of the possible increase in output if firms operate efficiently, and their production is not limited by the availability of the variable factors of production (e.g. a value of 1.50 indicates that the capacity output equals 1.5 times the current observed output).
If we also desire to calculate capacity utilization (CU), we need to consider the possibility that the commonly used measure, observed output divided by capacity output, may be downward biased (Färe et al., 1989). The possibility for the conventional measure of CU to be downward biased is because the numerator in the traditional CU measure, observed output, may be inefficiently produced. Färe et al. (1989) demonstrate that an unbiased measure of CU may be obtained by dividing an output-oriented measure of technical efficiency corresponding to observed variable and fixed factor input usage by the technical efficiency measure corresponding to capacity output (i.e. the solution to problem (1)).
To obtain a measure of TE corresponding to observed input usage, Färe et al. (1989) suggest that TE of the jth firm, (q(xj)), may be obtained as a solution to a linear programming problem:
|
maxqlz q |
|
|
s.t.
|
|
|
|
(2) |
|
|
|
where the input vector x includes both the fixed and variable inputs.
Problems (1) and (2) are typical DEA problems which provide measures of technical efficiency from an output orientation (i.e. inputs are held constant and outputs are allowed to vary). Problem (1) provides a measure of TE, q1, which corresponds to full capacity production. Problem (2) provides a measure of TE, q2, which corresponds to technically efficient production given the usage of the variable inputs. The ratio of the two qs, q2/q1, is an unbiased measure of capacity utilization (Färe et al. 1989).
Solutions to problems (1) and (2) provide estimates of technical efficiency, capacity, capacity utilization, and optimal input utilization relative to a best practice frontier. The solutions are not indicative of absolute efficiency and capacity. Based on the solutions, we may only conclude that an observation depicts more or less efficient production or capacity relative to another observation (e.g. we find that using an identical level of fixed and variable inputs, one fishing vessel has a higher production than that of another fishing vessel; we may conclude that the vessel with the higher production was more technically efficiency than was the vessel with the lower production).
The Färe et al. (1989) approach is also limited because it provides only a short-run measure of capacity (i.e. capacity is calculated conditional on fixed factors). It is possible, however, to impose constant returns to scale and determine the optimal levels of the fixed factors that would approximately correspond to the long-run level of capacity. Alternatively, it is possible to assess the optimum levels of the fixed and variable factors that correspond to scale efficiency and use those levels as benchmarks for assessing capacity in the long-run. We defer these other possible approaches to future research because there is no comparative basis upon which to evaluate the corresponding results. More important, though, is that even if the approach cannot provide measures of capacity and capacity utilization for the long-run, it can still provide measures useful for determining the potential capacity removed with vessel reduction programmes. Also, it is highly probable that any capacity reduction programme implemented by resource managers would have additional constraints on the existing vessels such that capacity would not be allowed to increase in a short to intermediate time period.
In the case of fisheries, there is a question about whether or not resource levels should be included. By including resources, it is possible to calculate capacity conditional on resource levels. A conditional capacity is not, however, the notion of capacity which primarily interests resource managers. Managers typically want to know what is the potential maximum catch if resource conditions were not limiting; this measure provides a benchmark for evaluating excess harvesting capacity. There also remains an issue about whether or not resource levels, if they are to be included, should be included as nondiscretionary inputs rather than discretionary inputs; captains have little control of resource levels other than by area selection.
Other issues that could be considered with the DEA framework of Färe et al. (1989) include calculation of capacity output under various by-catch mitigation programs or habitat restoration policies. Adding by-catch to the problem simply requires reformulating the problem such that by-catch is treated as an undesirable output; this requires weak sub-vector disposability constraints. Alternatively, the problem may be specified in terms of directional distance functions.
The United States northwest Atlantic sea scallop, Placopecten magellanicus, fishery was traditionally one of the most important United States fisheries in terms of ex-vessel revenues. Prior to the imposition of extremely restrictive regulations in 1994 and 1995, only five to six species generated ex-vessel revenues higher than those associated with sea scallops. In 1995, the ex-vessel value of sea scallops ranked ninth relative to other species.
The northwest Atlantic sea scallop is harvested primarily from Georges Bank and various Mid-Atlantic resource areas. The primary gear type is the dredge. Small quantities of sea scallops, however, are harvested with a trawl net. The primary landed product form is meats. Only small quantities of sea scallops are landed in the shell. The fleet is mostly comprised of vessels which are 51 or more gross registered tonnes in size. Crew sizes per trip, prior to the more restrictive regulations of 1994 and 1995, were typically between nine and 12 individuals. The number of days at sea per trip, also prior to the more restrictive regulations of 1994 and 1995, varied by homeport. Vessels from New England and New Jersey ports typically made 11 to 14 day trips. Vessels from the more southern areas of the Mid-Atlantic (Virginia and North Carolina) typically had trips between 15 and 20 days.
The sea scallop fishery has been managed by the New England Fishery Management Council (NEFMC) since 1983. Prior to 1994, scallops were managed mostly by age-at-entry restrictions. Shucked meats were restricted to a maximum count of 33 meats per pound (MPP) plus a ten percent tolerance; trips in which the average meat count exceeded 36.3 were cited as being in violation of the meat count regulations. Trips for which 40 or more scallops out of a sample of 400 scallops landed in the shell were less than three and a half inches were cited as being in violation of the shell-height regulation.
The meat count regulations were considered to be inadequate to control overfishing (Kirkley and Du Paul, 1993). Moreover, the regulations did not adequately control access or the potential excess capacity. Crew could and did mix scallop meats of different sizes to comply with the meat count regulation; it only required a few large scallop meats to be mixed with a lot of small meats to comply with the regulations. Crew also soaked meats in water to increase their size, and thereby, also contributed to a quality problem. In 1994, the NEFMC imposed new regulations that restricted the number of days at sea per vessel per year. In addition, crew size was restricted to seven individuals; prior to these new regulations, there were no constraints on crew size and vessels routinely had nine to 12 individuals. Other regulations were implemented to affect the catchability of small scallops (e.g. the rings of dredges were increased from three to three and a half inches; rings could not be linked by more than one link; and chafing gear was prohibited).
It appeared that the new regulations would be adequate to rebuild the stock and allow most of the existing vessels to remain in the fleet. The Sustainable Fishing Act (SFA), however, was implemented, and it appeared that the new regulations would not be adequate to achieve the objectives of the SFA. In fact, preliminary analysis indicated that the number of days per vessel per year would have to be reduced to between 35 and 75 days. Analysis by Kirkley and DuPaul (1993) and Edwards (1997), however, revealed that the number of days required for a vessel to break even ranged from 140 to 175 days. The only apparent viable option was to reduce the number of vessels or capacity and reallocate the days at sea among the remaining vessels. There is thus a strong urgency to develop measure of capacity for the northwest Atlantic sea scallop fleet.
In this section, we discuss the data and potential problems of the data. We also outline the structure of analysis and reasons for selecting the structure.
Using a panel data set on ten scallop vessels, we calculate capacity, capacity utilization, and input utilization with and without resource levels. Our primary purpose of calculating capacity is to demonstrate one approach that may be easily used to assess capacity in fisheries, particularly when economic data are not available which is quite typical of fisheries. Our calculations are derived under variable returns to scale. We treat resource abundance as a discretionary input. The assumption that resource abundance is discretionary is questionable because captains do not have control of the resource levels. Captains do, however, have control over the selection of fishing areas and scallops are relatively immobile or stationary relative to geographic areas.
The panel data set contains observations on output and input levels, resource abundance, and characteristics indicative of the fixed factors. The data set is for the years 1987 through 1990 and corresponds to trip level activity. Data were directly obtained from settlement sheets provided by vessel owners. Output is measured in terms of pounds of sea scallop meats landed per trip. We have two variable inputs days at sea and crew size per trip. The fixed factors are vessel gross registered tonnage (GRT), engine horsepower, and dredge width in feet. Stock abundance is treated as an input even though it is more indicative of the state of technology. Stock abundance measures are fishery dependent, but were obtained from previous monitoring programmes in which vessels made one tow at the end of a trip in order to provide information about resource abundance, state of reproduction, and age-class distribution (Kirkley and DuPaul, 1989; Kirkley et al., 1995, 1998). Stock abundance is measured in terms of the number of baskets per standard tow.
The inputs are not typical of those considered in analyses of other industries (e.g. fuel and capital services). The inputs are, however, consistent with the way managers and fishery researchers typically consider the inputs for fisheries. Moreover, the inputs are those that have often been subject to fisheries regulation (e.g. allowable days at sea or maximum number of crew). Days at sea reflects capital, energy, materials, and labour. It may be considered as an intermediate output of the first stage of a nonseparable two-stage technology (Pollak and Wales, 1987). Crew size is a stock and not a flow variable, but the services may be assumed to be proportional to total crew size.
We initially calculate technical efficiency corresponding to full capacity. We solve problem (1) with and without resource abundance included. The solution to problem (1) without resource abundance provides a measure of the potential output that could be possible if only the fixed factors were constraining production. The fixed-factor conditional capacity measure provides a reference for assessing whether or not the vessel had excess harvesting capacity relative to what was actually harvested or could have been efficiently harvested. Next, we again solve problem (1), but subject to constraints on resource abundance. The solution to problem (1), with resource abundance included, provides a measure of capacity conditional on the fixed factors and resource abundance.
We next compare the two calculated capacity outputs to determine whether or not resource abundance or the fixed factors constrained output. Because of the nature of linear programming, adding additional constraints should reduce the value of the solution if the additional constraints are binding. If the two measures are equal, we can determine that the fixed factors and not the resource level constrained output.
The approach of Färe et al. (1989, 1994) provides useful information about capacity output per trip, but it does not provide a framework for assessing the actual capacity over a year for a fishing fleet. This limitation, however, is not because of the method, but rather because of fishing practices. In previous studies by Färe et al. (1989), capacity and CU were assessed using annual production information for industries that would be expected to operate a relatively fixed number of days per year (e.g. electric utilities). Unlike many conventional industries that operate between 260 and 365 days a year, vessels do not always make the same number of trips or fish the same number of days a year. In fact, even the length of trips may be quite variable because of economic conditions or unforeseen events such as weather and medical and mechanical emergencies at sea.
Table 1. Annual production, days at sea, and average days and crew size per trip of ten mid-Atlantic sea scallop vessels
| |
|
1987 |
1988 |
1989 |
1990 |
|
Vessel 1: |
Production |
200 775 |
178 034 |
146 944 |
163 323 |
| |
Days at sea |
249 |
262 |
247 |
263 |
| |
Days per trip |
16.60 |
14.55 |
14.53 |
20.23 |
| |
Crew per trip |
10.47 |
9.67 |
9.47 |
9.15 |
|
Vessel 2:a |
Production |
101 656 |
|
|
|
| |
Days at sea |
148 |
|
|
|
| |
Days per trip |
9.87 |
|
|
|
| |
Crew per trip |
11.60 |
|
|
|
|
Vessel 3: |
Production |
150 832 |
124 401 |
117 993 |
117 707 |
| |
Days at sea |
242 |
245 |
253 |
254 |
| |
Days per trip |
10.52 |
16.33 |
15.81 |
15.88 |
| |
Crew per trip |
10.91 |
9.93 |
9.25 |
8.68 |
|
Vessel 4: |
Production |
81 794 |
156 419 |
153 199 |
171 494 |
| |
Days at sea |
112 |
242 |
267 |
285 |
| |
Days per trip |
14.00 |
15.13 |
16.69 |
20.35 |
| |
Crew per trip |
9.75 |
10.19 |
10.44 |
9.43 |
|
Vessel 5: |
Production |
143 150 |
141192 |
129 642 |
129 389 |
| |
Days at sea |
228 |
262 |
265 |
268 |
| |
Days per trip |
14.25 |
14.56 |
13.95 |
19.14 |
| |
Crew per trip |
10.25 |
9.61 |
9.47 |
9.14 |
|
Vessel 6: |
Production |
140 533 |
165 499 |
129 453 |
137541 |
| |
Days at sea |
190 |
267 |
254 |
246 |
| |
Days per trip |
11.88 |
16.69 |
14.11 |
17.57 |
| |
Crew per trip |
9.75 |
9.13 |
9.22 |
9.64 |
|
Vessel 7: |
Production |
211 532 |
164 037 |
143 554 |
160 576 |
| |
Days at sea |
260 |
263 |
253 |
259 |
| |
Days per trip |
17.33 |
17.53 |
16.87 |
18.50 |
| |
Crew per trip |
9.67 |
9.07 |
8.73 |
8.71 |
|
Vessel 8: |
Production |
164 566 |
140 333 |
127 165 |
136 992 |
| |
Days at sea |
228 |
254 |
251 |
243 |
| |
Days per trip |
14.25 |
16.93 |
15.69 |
16.20 |
| |
Crew per trip |
10.13 |
9.33 |
9.56 |
8.13 |
|
Vessel 9: |
Production |
152 841 |
142 949 |
114 039 |
138 701 |
| |
Days at sea |
198 |
264 |
270 |
238 |
| |
Days per trip |
16.50 |
16.50 |
14.21 |
14.88 |
| |
Crew per trip |
10.33 |
9.50 |
9.89 |
9.13 |
|
Vessel 10: |
Production |
128 031 |
139 334 |
98 500 |
152 797 |
| |
Days at sea |
186 |
271 |
216 |
267 |
| |
Days per trip |
12.40 |
15.06 |
14.40 |
16.69 |
| |
Crew per trip |
10.20 |
10.11 |
9.47 |
8.40 |
a Vessel Number 2 left the fishery in October, 1987.
In 1987, the average total number of days per vessel per year equalled 223 (Table 1). In 1988, the average total number of days per vessel increased to 259; the average total number of days declined to 153 in 1989. In 1990, the average total number again increased 258 days per vessel per year. Between 1987 and 1990, the actual number of days per year per vessel varied from a low of 112 for vessel #4 in 1987 to a high of 285 days for the same vessel in 1990. The number of days at sea per trip ranged from a low of three to a high of 26. Crew size per trip ranged from a low of seven to a high of 13. Most of the vessels took between 12 and 18 trips per year.
The actual number of days varies in accordance with a wide variety of factors (e.g. weather, regulations, family ties, economic factors such as prices and costs, availability of labour, and numerous other possible factors). The ten vessels are relatively homogeneous in terms of characteristics, and they all faced identical economic conditions such as output prices and factor costs. They all fished the same areas and thus encountered similar weather conditions. What are some possible reasons for the differences in the number of days per year per vessel?
In some cases, differences may be attributed to unscheduled maintenance (e.g. blown engine, broken winches, faulty electronics, etc.). In other cases, differences may reflect the preferences of captains; some captains are willing to work only so many days a year (Gautam et al., 1995). In other cases, economic and social factors may explain reasons for the differences. The only way to accurately determine the maximum potential number of days is to conduct very extensive economic and social surveys and analysis.
While detailed economic and social surveys and analyses may provide the information necessary for adequately determining the potential maximum number of days per year, such surveys and studies are costly and would likely lead to decision rules for determining the number of days rather than upper limits on the potential number of days (e.g. in years when abundance and output prices are high and fuel prices are low, vessel operators may decide to fish 260 to 280 days a year). Moreover, management agencies are unlikely to wait until such surveys and analyses have been completed before implementing capacity reduction programmes. In the interim, and based strictly on empirical observation, it is suggested that capacity output be determined based on two limits: (1) the observed maximum number of days per year per vessel; and (2) the average number of days per vessel per year.
In our panel data set, the observed maximum number of days was 285 which occurred in 1990 for vessel #4. Given the relatively homogeneity of vessel characteristics, we assume that all vessels could operate at least 285 days a year in each year. Based on the optimum days at sea per trip per vessel, we calculate the capacity output for each year by multiplying the capacity output per trip per vessel times the number of trips which could be taken using 285 days at sea per year and the optimum number of days per trip subject to resource and no resource constraints.
Our calculation of capacity output subject to resource conditions is somewhat complicated. In addition to incorporating an upper limit on the total number of days a year a vessel may be at sea, it is also necessary to incorporate limits on the number of days a vessel may fish within a shorter interval of time (e.g. if a vessel is already working 28 to 30 days a month, we cannot assess capacity by allowing another trip in that month). Alternatively, it becomes necessary to consider the possible reorganization of fishing practices (e.g. taking trips in different months or by determining whether or not it would have been possible for a vessel operator to take another trip within a given month).
Initially, the assessment of capacity output is restricted to those observations having the highest capacity output (i.e. data are sorted by boat capacity output in descending order). The optimal number of days are summed over that time period and compared to the maximum number of days. If the total number of optimal days exceeds 285, trips of optimal length and minimum capacity output are removed from the analysis until the total number of days equals 285. If the total number of optimal days is less than 285, trips of optimal length are added to the analysis until the total days at sea equals 285; the additional trips are added only to those periods for which it actually would have been possible for the vessel to have made a trip. The total number of optimal days at sea per trip per vessel per year may not exactly equal 285 for all vessels because of the use of empirically determined optimal days per trip (e.g. a vessel operator could take one more trip of 18 days and realize the capacity output, but that 18 day trip might cause the total number of optimal days to equal 287).
The average number of days per year per vessel between 1987 and 1990 equalled 248.25 days. We thus use 248.25 days and the optimum number of days for each vessel to calculate capacity output with and without resource constraints. The calculation of capacity output with resource constraints subject to an upper limit on days equal to the average number of days is done using the same procedures as stated in the previous paragraph.
We also calculate technical efficiency based on the solutions to problem (2) with resources included. This provides a measure of technical efficiency and the potential output that could be produced if production was efficient given different levels of resource abundance (i.e. the potential maximum output conditional on variable and fixed factor levels and resource abundance). It also provides the required numerator, q2, for calculating capacity utilization (i.e. CU = q2/q1).
In the following section, the empirical results and analysis are presented. We initially present and discuss the empirical measures of capacity. We next discuss input utilization levels relative to the full capacity output level. We also provide a discussion of the need to consider resource abundance when calculating capacity. Last, we conclude with a discussion of capacity utilization.
Examination of the solutions to the various DEA problems reveals that the fleet did have the capability to harvest considerably more than what was actually harvested between 1987 and 1990. In 1987, the fleet landed 1.48 million pounds (Table 2). Had the vessels efficiently used their variable inputs (problem 2), the catch could have been approximately 2.08 million pounds. If the fleet had operated at full capacity in 1987 over 285 days, but subject to resource limitations, it could have harvested 3.08 million pounds. Alternatively, if the fleet had operated at full capacity subject to resource limitations, but at the mean number of days of 248.25, the fleet had the potential to harvest 2.73 million pounds. If the fleet had operated at full capacity without resource limitations, but spent 285 days at sea, it had the capacity to harvest 3.48 million pounds. Operating at the mean number of total days per year per vessel of 248.25 and without resource limitations, the fleet had the potential to harvest 3.01 million pounds.
Overall, if vessels had operated efficiently they could have increased their total production of scallop meats by approximately 50.8 percent between 1987 and 1990. Improvements in just technical efficiency, given resource levels, could have increased production to 37.5 percent of capacity output in 1987, 62.6 percent in 1988, 38.0 percent in 1989, and 46.7 percent in 1990. Operating at the optimum level of days at sea and crew size and over 285 days, subject to resource conditions, would have allowed production to increase by another 39.9 percent between 1987 and 1990.
Presently, there are approximately 175 full-time vessels operating in the northwest Atlantic sea scallop fishery. In 1996, there were 82 vessels of the same size class (Tonnage class III which is 51 to 150 gross registered tonnes (GRT)) as those of the panel data set operating in the fishery. There were 132 vessels of the next size class (> 150 GRT) operating in the fishery. There were 120 vessels of the smallest documented size class (5 to 50 GRT). The long-term potential catch has been estimated to equal approximately 29.3 million pounds of meats (Northeast Fisheries Science Center, 1998). Recent information by a group of stock assessment scientists charged with defining allowable harvests and the levels of nominal catch corresponding to overfishing, however, suggests a sustainable harvest of approximately 20 million pounds per year (NEFSC, 1997). If only the 82 vessels are considered, they have a potential capacity output of approximately 29 million pounds if allowed to operate 285 days a year. If all tonnage class III and IV vessels are considered, they have a potential capacity output well in excess of 76.7 million pounds[144]. There should be little doubt that the sea scallop fishery does, in fact, have substantial excess harvesting capacity relative to proposed long-term or sustainable yields.
Table 2. Average performance and input usage, technical efficiency, and potential capacity output
|
Variable |
1987 |
1988 |
1989 |
1990 |
|
Average catch per trip |
9 773 |
9 199 |
7 685 |
9 913 |
|
Average stock abundance per trip |
3.31 |
2.81 |
2.43 |
2.70 |
|
Average technical efficiency per trip |
1.74 |
1.96 |
2.55 |
1.81 |
|
Average capacity efficiency with stock abundance |
3.94 |
3.39 |
6.50 |
4.43 |
|
Average capacity efficiency without stock abundance |
5.29 |
3.94 |
7.98 |
5.30 |
|
Average output per trip-technically efficient production |
13 770 |
15 098 |
13 744 |
14 675 |
|
Average output per trip capacity with resource levels |
20 135 |
20 332 |
19 414 |
19 722 |
|
Average output per trip-capacity without resource levels |
23 061 |
23 260 |
23 260 |
23 260 |
|
Average days per trip |
13.52 |
15.85 |
15.07 |
17.60 |
|
Optimal days per trip (with stock) |
18.76 |
19.14 |
18.97 |
19.15 |
|
Optimal days per trip (without stock) |
19.02 |
19.02 |
19.02 |
19.02 |
|
Average crew per trip |
10.36 |
9.63 |
9.51 |
8.92 |
|
Optimal crew per trip (with stock) |
11.46 |
11.22 |
11.00 |
11.11 |
|
Optimal crew per trip (without stock) |
12.99 |
12.99 |
13.04 |
13.07 |
|
Total actual catch (million pounds) |
1.48 |
1.35 |
1.16 |
1.30 |
|
Potential catch (million pounds) Technically efficienta |
2.08 |
2.22 |
1.73 |
1.94 |
|
Potential catch (million pounds) Capacity with stockb |
3.08 |
2.74 |
2.66 |
2.67 |
|
Potential catch (million pounds) Capacity without stockc |
3.46 |
3.13 |
3.13 |
3.13 |
|
Potential catch (million pounds) Capacity with stockd |
2.73 |
2.41 |
2.34 |
2.36 |
|
Potential catch (million pounds) Capacity without stocke |
3.01 |
2.72 |
2.72 |
2.72 |
a The fleet output if vessels operated efficiently using the same level of inputs. b The fleet output if the vessels operated efficiently and at full capacity (285 days) given resource levels. c The fleet output if the vessels operated efficiently and at full capacity (285 days) without resource limits. d The fleet output if the vessels operated efficiently and at full capacity (248.25 days) given resource levels. e The fleet output if the vessels operated efficiently and at full capacity (248.25 days) without resource limits.
The average actual catch, number of days, and crew size per trip in 1987 were 9773 pounds, 13.52 days, and 10.36 crew in 1987. Results suggest that the average optimum number of days and crew per trip should have been 19.02 and 18.76 days and 13.02 and 11.46 crew without and with stock abundance included in the analysis[145]. In 1987, 51 out of 151 trips had more than 18 days at sea, while 72 trips had crew sizes larger than or equal to 11 individuals. If the number of trips with days less than ten are eliminated from the average, the average number of days per trip increases to 17.36; 92 percent of the vessels had trips longer than ten days in 1987. The corresponding average capacity output, constrained only by the fixed factors, per trip in 1987 is estimated to equal 23 061 pounds of scallop meats. If we consider the potential output with respect to only improvements in technical efficiency, but using the same level of inputs as observed, the potential output per trip is estimated to equal 13 770 pounds. The potential capacity output per trip, subject to resource constraints, is estimated to equal 20 135 pounds.
A more detailed examination of the full capacity utilization of days at sea and crew size per trip reveals that very few trips operated at the full capacity utilization levels between 1987 and 1990 (Table 3). In 1987, only seven trips, conditional on resource levels, had the full capacity utilization number of days and optimum crew size. With respect to the full capacity limitations, zero trips had the optimum levels. With respect to only the optimum days at sea, 39.1 percent of all trips between 1987 and 1990 had days at sea within plus or minus one day of the optimum given resource levels. The number of trips within plus or minus one individual of the optimum crew size, given resource conditions, was only 22 percent between 1987 and 1990. With respect to the full capacity output without resource constraints, only 14.8 and 2.2 percent of all trips between 1987 and 1990 had, respectively, the optimum days and crew size.
Table 3. Number of trips with full utilization levels of days at sea and crew size
| |
1987 |
1988 |
1989 |
1990 |
|
With Resource:a |
|
|
|
|
|
Observed Days = Optimum Days |
17 |
22 |
15 |
15 |
|
Observed Crew = Optimum Crew |
12 |
2 |
5 |
3 |
|
Both Optimum |
7 |
0 |
2 |
3 |
|
Without Resource:b |
|
|
|
|
|
Observed Days = Optimum Days |
18 |
30 |
19 |
19 |
|
Observed Crew = Optimum Crew |
0 |
1 |
0 |
0 |
|
Both Optimum |
9 |
2 |
0 |
2 |
|
Number of Trips for whichc |
|
|
|
|
|
18 £ Observed Days £ 20 |
50 |
68 |
49 |
60 |
|
11 £ Crew Size £ 13 |
55 |
22 |
29 |
9 |
|
Total Number of Trips |
151 |
147 |
151 |
132 |
a With resource abundance included in the analysis of capacity, 552 observations had a calculated optimum number of days between 18 and 20, and 444 observations had a calculation optimum crew size between 11 and 13. b Without resource abundance, 581 observations had a calculated optimum number of days between 18 and 20, but only 286 observations had a calculated optimum crew size between 11 and 13. c Eighteen to twenty days represents the approximate range of the full capacity number of days, and 11 to 13 crew represents the range of the full capacity crew size. level of days at sea and crew, without resource
We also found differences in the various potential output and optimum input levels over time. This was because of how potential output was calculated, the exit of one vessel in October 1987, and varying resource conditions between 1987 and 1990. Since the analysis was conducted on a per trip basis, the potential output was calculated by multiplying the number of trips times the respective potential output. In 1987, the ten vessels made 151 trips. In 1988, there were only nine vessels and they made a total of 147 trips. The number of trips in 1989 and 1990 were, respectively, 151 and 132. In the calculation of the two capacity outputs, the calculations were always based on the maximum 285 observed days at sea or the average 248.25 days at sea.
There was a relative consistency between resource abundance and the levels of the potential output under technically efficient production and capacity production conditional on resources levels. Average abundance per trip declined between 1987 and 1989, and the actual and capacity output, conditional on resource abundance, also declined. Between 1987 and 1990, there also was some apparent substitution between days at sea and crew size. The number of days per trip increased while the crew size decreased (e.g. the average number of days and crew size per trip in 1987, respectively, equalled 13.52 and 10.36; in 1990, the average number of days and crew size per trip, respectively, equalled 17.60 and 8.92). Reasons for the changes may be related to numerous factors which are not considered in the analysis (e.g. an increase in the abundance of larger scallops might motivate captains to increase their days at sea per trip, but also to decrease the crew size since less crew would be needed to shuck large scallops).
What about the possibility that the controllable fixed factors rather than resource abundance constrained capacity output? Out of a total of 581 trips made by the ten vessels between 1987 and 1990, only 25 trips were not constrained by resource conditions. Alternatively, the potential capacity output was constrained by resource levels for 556 trips. Those trips for which the potential capacity output conditional on resource abundance equalled the potential capacity output without resource abundance were associated with very high stock levels. The mean stock abundance index for trips in which the capacity output conditional on resource levels equalled the capacity output without resource abundance was 5.37 baskets per tow; the corresponding range was 4.26 to 6.85 baskets per tow. For those trips for which the capacity outputs were not equal, the mean stock abundance index was 2.70 baskets per tow, and the corresponding range was 0.28 to 4.25 baskets. The largest number of trips for which resource abundance would not constrain output occurred in 1987. In 1987, the capacity output for 23 trips would not have been constrained by resource abundance. The potential capacity output for all trips in 1988 would have been constrained by resource levels. The potential capacity output for only one trip in 1988 and one trip in 1989 would not have been constrained by resource abundance.
A remaining issue is that of capacity utilization. Färe et al. (1989) calculated CU by taking the ratio of the output-oriented technical efficiency measure to the output oriented capacity technical efficiency measure. Given the various possibilities because of the possible number of days at sea and the various possible groupings, we report CU measures on a per vessel basis and for each year between 1987 and 1990 (Table 4). Unfortunately, our CU measures may pose some problems. The calculation of CU was over all observations. If vessel operators actually operated at full capacity utilization, they would require more days than are available in a year. We thus calculate CU conditional our days at sea limits of 285 (maximum observed)[146]. We provide measures of CU with and without resource abundance included in the analysis and with respect to the observed and technically efficient output.
Table 4. Average capacity utilization per vessel conditional on vessel operating 285 days per year
|
Vessel |
1987 |
1988 |
1989 |
1990 |
||||
| |
Observeda |
Efficientb |
Observed |
Efficient |
Observed |
Efficient |
Observed |
Efficient |
|
With Resource:c |
|
|
|
|
|
|
|
|
|
1 |
60.7 |
85.6 |
55.2 |
82.3 |
47.1 |
80.1 |
51.5 |
76.7 |
|
2 |
40.4 |
45.9 |
|
|
|
|
|
|
|
3 |
49.7 |
71.6 |
45.4 |
77.3 |
46.6 |
78.1 |
47.0 |
69.3 |
|
4 |
26.9 |
39.6 |
48.9 |
82.1 |
48.5 |
87.6 |
54.7 |
80.2 |
|
5 |
49.0 |
71.2 |
53.4 |
85.6 |
49.3 |
74.5 |
51.0 |
77.1 |
|
6 |
44.0 |
64.6 |
51.9 |
80.4 |
41.8 |
75.5 |
44.7 |
73.4 |
|
7 |
64.6 |
81.4 |
51.9 |
76.7 |
45.7 |
70.5 |
51.7 |
69.1 |
|
8 |
52.3 |
77.5 |
45.2 |
76.5 |
41.8 |
79.6 |
46.1 |
64.4 |
|
9 |
48.0 |
67.3 |
46.5 |
80.9 |
38.3 |
86.8 |
44.6 |
73.2 |
|
10 |
40.8 |
64.9 |
45.3 |
87.3 |
33.4 |
67.8 |
49.0 |
71.8 |
|
Fleet |
48.0 |
67.6 |
49.3 |
81.0 |
43.6 |
77.9 |
49.0 |
72.5 |
|
Without Resource:d |
|
|
|
|
|
|
|
|
|
1 |
56.0 |
79.1 |
46.7 |
74.0 |
41.0 |
69.7 |
45.6 |
65.2 |
|
2 |
30.5 |
34.6 |
|
|
|
|
|
|
|
3 |
45.2 |
65.1 |
37.3 |
63.5 |
35.4 |
59.4 |
35.3 |
52.0 |
|
4 |
22.8 |
33.6 |
43.7 |
73.2 |
42.8 |
77.3 |
47.9 |
70.2 |
|
5 |
42.9 |
62.4 |
42.3 |
67.8 |
38.9 |
58.7 |
38.8 |
58.7 |
|
6 |
40.1 |
58.9 |
47.2 |
73.1 |
37.0 |
66.7 |
39.3 |
64.4 |
|
7 |
59.0 |
74.4 |
45.8 |
67.7 |
40.0 |
61.7 |
44.8 |
59.9 |
|
8 |
47.9 |
71.0 |
40.8 |
69.1 |
37.0 |
70.4 |
39.9 |
55.6 |
|
9 |
42.6 |
59.7 |
39.9 |
69.5 |
31.8 |
72.0 |
38.9 |
63.5 |
|
10 |
36.4 |
57.8 |
39.6 |
76.3 |
28.0 |
56.7 |
43.4 |
63.5 |
|
Fleet |
42.4 |
59.7 |
43.0 |
70.5 |
36.9 |
66.0 |
41.6 |
61.6 |
a Capacity utilization calculated as the ratio of observed output to the capacity output conditional on 285 days a year. b Capacity utilization calculated as the ratio of technically efficient output to the capacity output conditional on 285 days a year. c Capacity output determined conditional on resource abundance and other fixed factors. d Capacity output determined without resource abundance.
Overall, we find that average capacity utilization per trip, when based on observed output and resource constraints, is quite low. When CU is assessed using the technically efficient output in the numerator, CU is relatively high. Technical inefficiency appears to be a major reason why vessels have not operated near optimal capacity. Alternatively, if we restricted our analysis of CU to the ratio of observed output divided by capacity output, we would have a substantial downwards bias in our assessment relative to the frontier output (Färe et al., 1989). In general, vessel operators have tended to take shorter trips than they should have if they were to operate at the optimal capacity. CU conditional on resource abundance and observed output ranged from 26.9 for vessel 4 in 1987 to 54.7 in 1990; when considered relative to the technically efficient output level, CU ranged from 39.6 for vessel 4 in 1987 to 80.2 for vessel 4 in 1990. When CU is assessed without resource abundance, CU is alarmingly lower. In 1987, CU for vessel 4, when calculated using observed output, was 22.8; CU for vessel 4 in 1990 was only 47.9. Similarly, CU for vessel 4, when calculated using the technically efficient output level was only 33.6 in 1987 and only 70.2 in 1990.
If we consider CU relative to the observed number of days per year, CU is considerably higher. CU conditional on resource abundance and calculated using the technically efficient output and observed number of days ranged from a low of 72.2 for vessel 2 in 1987 to a high of 96.6 for vessel 1 in 1987; in 1990, CU ranged from 72.5 for vessel 8 to a high of 85.3 for vessel 9.
The approach of Färe et al. offers one viable way to assess capacity, capacity utilization, and input utilization in a fishery. Although it is production or primal oriented, it does provide information that may be extremely useful to resource managers. In addition, it provides information consistent with the way many resource managers view capacity (i.e. what could an existing fleet harvest in the absence of regulatory or resource constraints?). Last, it offers a more complete basis for calculating capacity than the commonly-used measure of number of vessels in a fishery (NEFSC, 1998).
The approach, however, also has some limitations. First, because it is production oriented, it does not adequately reflect the underlying economics. That is, economic conditions may be the reason why a firm does not operate at capacity; alternatively, the approach does not readily allow the determination of the economic conditions under which a firm would operate at capacity. As shown by Berndt and Fuss, though, the economic measure may be indeterminate in the presence of multiple fixed or quasi-fixed factors. Recently, Färe and Grosskopf (1998) developed a possible DEA approach that does allow for calculating the economic concept of capacity. Their approach has not, however, been empirically applied, and would not likely have widespread applicability in fisheries because of the absence of data on production costs. Moreover, it is not known if the recent Färe and Grosskopf approach adequately solves the indeterminancy problem associated with multiple fixed factors. Second, in the case of multiple outputs, which are quite common to many fisheries, capacity output is calculated based on a radial expansion of all outputs. It is possible that this limitation could be corrected by considering a non-radial expansion of outputs (Färe et al., 1994).
Regarding the sea scallop fishery, our limited empirical analysis revealed that there was substantial excess harvesting capacity by the ten vessels which comprised the panel data set and relative to the entire fleet. We also found that technical inefficiency and sub-optimal levels of variable inputs were two major reasons why many of the vessels did not operate near full capacity utilization. For most of the vessel trips, we determined that resource levels and not the fixed factors constrained capacity output between 1987 and 1990.
Our analysis also provided results somewhat consistent with the current recommendations of a national team of scientists charged with determining the optimal level of catch and the corresponding reduction in fishing vessel effort. The national team has recommended that the annual harvest of sea scallops should be limited to approximately 20 million pounds. In order to accomplish this objective, the national team has suggested that the annual number of days which vessels fish should be reduced by approximately 60 percent. If converted into simple average catches conditional on number of days, the number of vessels that could produce the equivalent recommended harvest is approximately 65. Our results would suggest a fleet of 56 or fewer vessels could harvest the recommended 20 million pounds. Differences are associated with the explicit calculation of capacity, recognition of different vessel size classes, and the fact that the national team used average catches and the assumption that the relationship between fishing mortality and days at sea is constant, regardless of different size vessels. Finally, we offer that although the approach of Färe et al. has limitations, it does offer information that could be particularly useful to resource managers concerned with developing buyback or fleet downsizing programmes.
Apostle, R., McCay, B. & Mikalsen, K. 1993. Overcapacity and Privatization: The Case of ITQs in the Scotia-Fundy Groundfish Fisheries. Paper presented to the Twelfth Anniversary Conference of the International Society for the Study of Marginal Regions. University College, Swansea and Gregynog, Powys.
Augstyn, J. 1996. Government Policies to Match Fleet Capacity to Available Marine Resources. Memo to Fisheries Department, Food and Agriculture Organization of the United Nations, from Sea Fisheries, Department of Environmental Affairs, Government of South Africa, Capetown.
Ballard, K. & Roberts, J. 1977. Empirical Estimation of the Capacity Utilization Rates of Fishing Vessels in 10 Major Pacific Coast Fisheries. Washington, D.C.: National Marine Fisheries Service.
Banks, R. 1977. Adjustments to Capacity in the European Union. Paper prepared for F.A.O. Fisheries Department.
Battese, G.E. & Coeli, T.J. 1995 A Model for Technical Inefficiency Effects in a Stochastic Frontier Production Function for Panel Data. Empirical Economics 20:325-332.
Berndt, E.R. & Fuss, M.A. 1989. Economic Capacity Utilization and Productivity Measurement for Multiproduct Firms with Multiple Quasi-Fixed Inputs. National Bureau of Economic Research Working Paper No. 2932. Cambridge, Mass.: National Bureau of Economic Research.
Christy, F.T. 1996. Over Capacity in Fisheries: Problems and Approaches. Washington, D.C.: IMARIBA.
Edwards, S. 1997. Preliminary Analysis of Economic Returns from Different Allocations of Days at Sea in the Northwest Atlantic Sea Scallop Fishery. Northeast Fisheries Science Centre, National Marine Fisheries Service).
Färe, R. 1984. The Existence of Plant Capacity. International Economic Review 23: pp. 209-213.
Färe, R., Grosskopf, S. & Kokkenlenberg. E. 1989. Measuring Plant Capacity Utilization and Technical Change: A Nonparametric Approach. International Economic Review 30: pp. 655-666.
Färe, R. Grosskopf, S. & Lovell, C.A.K. 1994. Production Frontiers. New York: Cambridge University Press.
Färe, R., & Grosskopf, S. 1998. Primal and Dual DEA Measures of Capacity Utilization. Dept. of Econ. And Dept. of Agri. And Res. Economics Discussion Paper, Oregon State University.
FAO. 1998. Report of the Technical Working Group on the Management of Fishing Capacity. La Jolla, United States, 15-18 April 1998. FAO Fisheries Report No. 586. Rome, FAO.
Gautam, A., Strand, I. & Kirkley. J.E. 1996. The Backward Bending Supply of Labour. J. Env. Econ. And Man. 31: pp. 352-367.
Johansen, L. 1968. Production Functions and the Concept of Capacity. Recherches Récentes sur la Fonction de Production, Collection, Economie Mathématique et Econométrie 2.
Kirkley, J.E. & Du Paul, W.D. 1989. Science, Commercial Practices, and the Determination of Fishery Regulations. Journal of Shellfish Research 8: pp. 139-149.
Kirkley, J.E. & Du Paul. W.D. 1993. Elimination of the Meat Count Standard: A Preliminary Assessment of Impacts. Prepared as contract report for Mid-Atlantic Fisheries Management Council.
Kirkley, J.E., Squires, D.E. & Strand, I.E. 1995. Technical Efficiency in Commercial Fisheries. Amer. J. Agr. Econ. 77: pp. 686-697.
Kirkley, J.E., Squires, D.E. & Strand, I.E. 1998. Characterizing Managerial Skill and Technical Efficiency in a Fishery. J. Productivity Analysis 9: pp.145-160.
Kirkley, J.E. & Squire, D. 1999. Measuring Capacity and Capacity Utilization in Fisheries. In: Gréboval, D (Ed). Managing Fishing Capacity: Selected Papers on Underlying Concepts and Issues. FAO Fisheries Technical Paper No 386. pp. 75-200. Rome, FAO.
Klein, L.R. & Summers, R. 1966. The Wharton Index of Capacity Utilization. Philadelphia: University of Pennsylvania, Studies in Economics.
Mace, P. 1996. Developing and Sustaining World Fishery Resources: The State of Science and Management. Paper delivered to the World Fisheries Congress, Brisbane.
Morrison, C. 1985a. Primal and Dual Capacity Utilization: An Application to Productivity Measurement in the United States Automobile Industry. Journal of Business and Economic Statistics 3: pp. 312-324.
Morrison, C. 1985b. On the Economic Interpretation and Measurement of Optimal Capacity Utilization with Anticipatory Expectations. Review of Economic Studies 52: pp. 295-310.
Morrison, C. 1986. Productivity Measurement with Non-Static Expectations and Varying Capacity Utilization. Journal of Econometrics 33: pp. 51-74.
Nelson, R. 1989. On the Measurement of Capacity Utilization. Journal of Industrial Economics XXXVII (3): pp. 273-286.
North East Fisheries Science Centre 1997. Report of the 25th Northeast Regional Stock Assessment Workshop (25th SAW): Stock Assessment Review Committee (SARC) Consensus Summary of Assessments. [By Northeast Regional Stock Assessment Workshop No. 25.] December 1997. CRD 97-14. NOAA: United States.
North East Fisheries Science Centre 1998. Report of the 27th Northeast Regional Stock Assessment Workshop (27th SAW): Stock Assessment Review Committee (SARC) Consensus Summary of Assessments. [By Northeast Regional Stock Assessment Workshop No. 27.] December 1998. CRD 98-15. NOAA: United States.
Pollak, R.A. & Wales, T.J. 1987. Specification and Estimation of Nonseparable Two-Stage Technologies: The Leontief and the Cobb Douglas CES. J. Polit. Econ. 95: pp. 311-333.
United States Congress. 1996. The Sustainable Fishing Act. Washington, D.C.
Valatin, G. [no date] The Impact of a Decommissioning Scheme on Aggregate Fishing Effort: The Variability in Effort of Similar Boats. Economics Unit, Sea Fish Industry Authority: Edinburgh.
| [137] College of William
and Mary, School of Marine Science, Gloucester Point, VA 23062. Email: [email protected].
Support for this work provided by the College of William and Mary, School
of Marine Science, Virginia Institute of Marine Science, Gloucester Point,
Virginia United States 23062, and The Reves Center for International Studies,
College of William and Mary, Williamsburg, Virginia. United States. [138] Department of Economics, and Department of Agricultural and Resource Economics, Oregon State University, Corvallis, OR 97331-3612. [139] Department of Economics, Oregon State University, Corvallis, OR 97331-3612. [140] Department of Agricultural and Resource Economics, University of Maryland, College Park, MD 20742. [141] Southwest Fisheries Science Center, National Marine Fisheries Service, La Jolla, California 92038. [142] Department of Agricultural and Resource Economics, University of Maryland, College Park, MD 20742. [143] Kirkley and Squires (1999) provide an extensive discussion and listing of various approaches and previous research on capacity and capacity utilization in fisheries. [144] The estimate of fleet capacity is based on the assumption that capacity output for tonnage class III vessels equals the capacity output for tonnage class IV and all vessels fish 285 days a year. Our estimate is likely to be substantially downward biased given that tonnage class IV vessels likely have considerably more capacity. [145] The term optimal level of inputs used in the text actually refers to the input usage at maximum potential capacity (Fare et al., 1989). [146] Measures of capacity utilization conditional on mean and observed number of days per year may be obtained from the authors. |