| AFRICAN REGIONAL AQUACULTURE CENTRE, PORT HARCOURT, NIGERIA | ARAC/87/WP/12(3) |
| CENTRE REGIONAL AFRICAIN D'AQUACULTURE, PORT HARCOURT, NIGERIA |
M. N. KUTTY
African Regional Aquaculture Centre
Port Harcourt, Nigeria
Lectures presented at ARAC for the Senior Aquaculturists course
UNITED NATIONS DEVELOPMENT PROGRAMME
FOOD AND AGRICULTURE ORGANIZATION OF THE UNITED NATIONS
NIGERIAN INSTITUTE FOR OCEANOGRAPHY AND MARINE RESEARCH
PROJECT RAF/82/009
JUNE, 1987
Hyperlinks to non-FAO Internet sites do not imply any official endorsement of or responsibility for the opinions, ideas, data or products presented at these locations, or guarantee the validity of the information provided. The sole purpose of links to non-FAO sites is to indicate further information available on related topics.
This electronic document has been scanned using optical character recognition (OCR) software. FAO declines all responsibility for any discrepancies that may exist between the present document and its original printed version.
5. EVAPORATION AND EVAPO-TRANSPIRATION
CHAPTER III
CLIMATIC FACTORS
Aquatic systems in which animals are reared are directly influenced by climate. We shall in this discussion review these factors and study their role in the aquatic environment especially with reference to the selection of sites for suitable aquaculture systems.
The temperature of the water is regulated mainly by the temperature of the surrounding air. Factors like the quantity of oxygen dissolved in the water, evaporation and also productivity, depend directly on the temperature of water. The temperature of the surrounding air is usually measured using a thermometer kept in a ventilated shelter which protects it from the sun, wind and rain. The shelter is built at a height between 1.50 m to 2 m above ground level covered with turf.
Generally the minimum temperature and the maximum temperature of the day are taken, the first measurement being done just before sunrise, around 5.30 – 6 a.m, and second immediately after the sun has passed the zenith i.e. around 1 or 2 p.m. The mean of the two values is taken as the daily average temperature.
A simpler way is to use a maximum-minimum thermometer which gives directly the maximum and the minimum temperature of the period of measurement.
The thermograph is even more accurate because it can give a continuous record of the variations of temperature during a given period. The variations are traced on a graph sheet fixed on a drum rotated by a clock mechanism. The thermograph can be a weekly or daily recording unit.
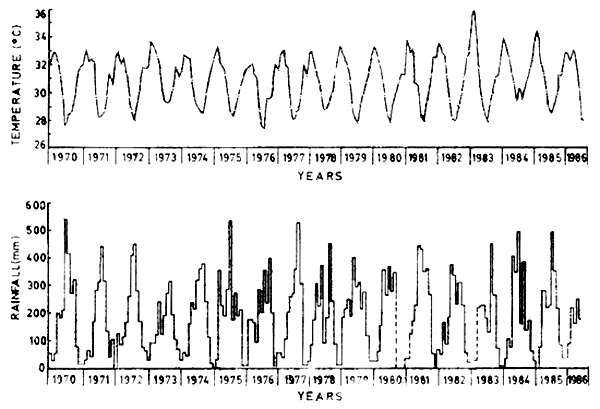
The daily temperature read over a period of one month or one year can be presented in a single graph to illustrate better the change of the temperature during that observed period. These readings can be taken at short intervals throughout the day in order to determine the daily cycle of temperature. The rate of change of temperature in atmosphere with altitude is called the lapse rate. The mean value is about 6.5 per 1000 M height change, being subject to change according to the specific situation. Mean monthly temperature and rainfall at Port Harcourt (04°51 N, 07° 01E, altitude 17.6 m) over a 16-year period (1970 to 86), from the records of pH Metereological Service, are shown in Fig. I.
Two separate aspects the photoperiod (duration of sunlight over the day) and light intensity should be considered as factors affecting aquaculture. In aquaculture, an important issue is the quantity of light that falls on the water; this regulates the development of plankton and therefore the availability of natural foods (phytoplankton, zooplankton etc.). The evaporation of water also is a result of light intensity and photoperiod (see below). Since the change os state of the molecules of water from liquid to gas requires energy, the process is most active under direct radiation of sun. It is obvious that clouds that cut down radiation will reduce energy input and reduce evaporation (see below). Metereological stations use the heliograph and radiometer for measuring photoperiod and the intensity of light respectively (see also “Light”, under “Physical features of water”).
Precipitation occurs mainly as rain but may also occur as hail, sleet, snow, fog or dew. Usually the total quantity of rain fall in a given period is expressed as the height of the water dropping down on horizontal plane without taking into account any loss due to water running out or loss by seepage and evaporation. The height obtained is usually expressed in millimetres. We take into consideration rain water as the main form of precipitation in the tropics, but precipitation from dew can be important in the arid regions.
Rains are caused by a condensation of the atmospheric water vapour following cooling of the air mass. Rainfall is measured with a rain guage which is a collector bottle cylindrical in shape, provided with a funnel with raised edge. The rain-water accumulate in the bottle, which has a narrow neck in order to reduce losses caused by evaporation. Rainfall can also be measured by automatic rain guages.
The rainfall data are taken normally every morning at the same hour of the day. The data are then plotted as a histogram which indicate the quantity of rainfall for specific unit of time. It is often important to be able to forecast the rains. It is also convenient to have the monthly average values established over a number of years. (see Fig. 1). In many cases, the change from average values from one year to another could be quite important. It is sometimes interesting to assess if during the years there have been dryness or if an increase of rainfall is to be expected. Appropriate methods to appreciate these variations in rainfall exist. For this effect, one has to refer to special publications (FAO, 1976).

Fig. 1. Mean monthly temperature and rainfall in Port Harcourt, Nigeria (04° 51'N,07° 01'E;
altitude, 17.6 m) over a 16-year period from 1970 – 1986. Numbers at bottom of
histogram indicate total annual rainfall (in mm) - Courtesy Mrs. J. Akiri and
Port Haros
The evaporation is the quantity of water transformed into atmospheric water vapour from a water body or from the ground. The transpiration is the loss of water from the surface of leaves of plants.
The evapo-transpiration includes the loss of water due to both the evaporation from the ground and the transpiration of plants. The evaporation is important in tropical aquaculture. This information enable us to determine the losses of water from the ponds, which is influenced by a number of factors. The surrounding temperature, the intensity of the light the wind and most importantly, the humidity in the air. The last-factor will depend on the evapo-transpiration of the environment surrounding the ponds.
The easiest method is to measure the evaporation in an open container filled with water. The container or tank can be of different shapes with a surface area varying from 0.2 to 2.00 m2 and with a depth of between 0.25 to 2 m. The measurements are taken in mm every day early in the morning.
The data obtained with this method are estimates of the potential evaporation. The real value of evaporation depends on several factors and is generally lesser than the potential evaporation.
Some empirical formula for calculation of evapo transpiration based on temperature relative humidity, wind and sun shine exist. Most of these formulae were established for temperated regions and perhaps not applicable elsewhere. Huet (1970) indicates an average daily evaporation of 2.5 cm for tropical regions. In the absence of more accurate values, this measure of 2.5 cm could be effectively used to calculate the volume of water to be replaced in the ponds to replace the loss incurred due to evaporation. If more precise measurements are required standard estimations (see Penman formula) should be looked into (see also “Water supply” in this section).
An example of estimation of evapo-transpiration by Penman method:
The formula for calculation of evaporation of an open water surface (Eo) was given by Penman. In view of the several difficulties, a very close approximation of Eo is given by the modified Penman formula for “Reference Evaporation” (ETo) (see FAO Irrigation and Drainage paper, No. 27). Eto indicates the rate of evapo-transpiration of an extended surface of an 18 to 15 cm tall grass cover, actively growing, completely shading the ground and not short of water. This ETo gives for our purposes of water requirement estimates in fish ponds, sufficient accurate estimate of Eo, without applying a correction.
Climatic data needed are: mean temperature (T in °C); mean relative humidity (RH in %); total wind run (U in Km/day at 2 m height) and mean actual sunshine duration (n in hour/day) or mean radiation (Rs or Rn equivalent evaporation in mm/day). Also day time windspeed (U day in m/sec at 2 m height) must be available. Also reference evapo-transpiration (ETo) representing the mean value in mm/day, over the period considered is obtained by:
ETo = c W. Rn + (1 - W). f(U). (ea - ed).,
| Where: | ||
| (ea - ed) | = | vapour pressure deficit which is the difference between saturation vapour pressure (ea) at T mean in m bar (Table 3.I) and actual vapour pressure (ed) in m bar where ed = ea. RH/100. |
| f(U) | = | wind function of f(U) = 0.27 (1 + U/100) with U in Km/day measured at 2 m height. |
| Rn | = | total net radiation in mm/day or Rn = 0.75Rs - Rnl where Rs is incoming shortwave radiation in mm/day either measured or obtained from Rs = (0.25 + 0.50 n/N)Ra. Ra is extra-terrestrial radiation in mm/day (Table 3.II), n is the mean actual sunshine duration in hour/day and N is maximum possible sunshine duration in hour/day (Table 3.III). Rnl is net longwave radiation in mm/day and is a function of temperature, f(T), of actual vapour pressure, f(ed) and sunshine duration f(n/N), or Rnl = f(T). f(n/N). f(ed) Tables 3.IV, 3.V and 3.VI) |
| W | = | temperature and altitude dependent weighting factor (Table 3.VII) |
| c | = | adjustment factor for ratio U day/U night, for RHmax and for Rs (Table 3.VIII). |
Example
Data given: Location 30°N; altitude 95 m; July; Tmean 28.5°C; RH mean 55%; U mean 232 Km/day; n mean 11.5 hour/day; (RHmax 80%, U day 3 m/sec, U day/U night 1.5).
Method of calculation:
| ea | T = 28.5°C | Table 3.I | 38.9 mbar |
| ed | ea. RH/100 | Calc | 21.4 mbar |
| ea-ed | Calc | 17.5 Mbar | |
| f(U) | 0.27(1 + U/100); U = 232 Km/day | Calc | 0.9 |
| Ra | 30°N, July | Table 3.II | 16.8 mm/day |
| N | 30°N, July | Table 3.III | 13.9 mm/day |
| Rs | (0.25 + 0.50 n/N) Ra | Calc | 11.2 mm/day |
| Rnl | f(T).f(ed).f(n/N) | Tables 3.IV, V, VI | 1.8 mm/day |
| Rn | 0.75Rs - Rnl | Calc | 6.6 mm/day |
| W | T = 28.5°C; 95 m | Table 3.VII | 0.77 |
| c | RHmax 80%; Rs 11.2; Uday/Unight 1.55 | Table 3.VIII | 1.01 |
| ETo | c(W. Rn + (1 - W). f(U).(ea - ed) | Calc | 8.8 mm/day |
(source: FAO, 1976)
Air easily absorbs moisture in the form of water vapour. The amount absorbed depends on the temperature of the air and of the water. The greater the temperature the more water vapour the air can contain. The water vapour exerts a partial pressure usually measured in either bars (1 bar = 105N/m2; 1 millibar = 102 N/m2) or mm height of a column of mercury (Hg) (1 mm Hg = 1.36 mbar).
The humidity in the air is an important climatic factor. It influences the evaporation of the water in the ponds. If the degree of humidity in the air is high, the evaporation will be less. Besides, the measurements of humidity will give an indication of action to be taken for the conservation of feed, manure, equipment etc. A high degree of humidity in the air will cause the increase in moisture of stocked agric products, prepared foods, and hardening of chemical manure, cement etc.
A measure of the degree of humidity in the air can be made with an hygrometer or a hygrograph. They both use the same principle. A human hair lengthens itself more or less according to the humidity of the air. The lengthning of the hair is transmitted to a needle which indicate the relative humidity on a standardized dial-plate. The change in the humidity during a given period (a day, a week) is recorded in a graph.
The wind influences the other meterological factors, evaporation, temperature humidity etc. By its strength alone, it can create waves on a water body and endanger structures, like pens or cages. It is therefore necessary to get information on wind direction and speed. Several corrective measures could then be envisaged. The speed of the wind and its direction are measured with anemometers made of 3 or 4 conical small cups mounted at the extremity of short mobile arms fixed on a vertical axis. The numbers of revolutions of the small cups around this axis per unit time give the speed of the wind. The weather cock indicate the direction of the wind.
Floods are seasonal phenomena happening frequently during rainy season in certain regions. The excess water supply due to rundown caused by the rainfall make water flow over their beds, flooding the nearby plains. The level and the seriousness of the flood should be noted. The height of the fish pond dike will therefore have to be calculated in order to avoid the flooding of the ponds, damages caused to the dykes and the loss of fishes. The buildings should also be sited taking into consideration the level of floods.
The infrastructure (buildings, cages, pens etc) will also have to be built taking into account the strength and the frequency of tornadoes and cyclones occurring severely in some regions (cyclonic season for example in Madagascar/Philippines).
FAO, 1976. Agro-Metereological stations. Bulletin of Irrigation and Drainage, No. 27, Rome.
Table 3.I: Saturation Vapour Pressure (ea) in mbar as Function of Mean Air Temperature (T) in °C*
| Temperature °C | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| ea mbar | 6.1 | 6.6 | 7.1 | 7.6 | 8.1 | 8.7 | 9.3 | 10.0 | 10.7 | 11.5 | 12.3 | 13.1 | 14.0 | 15.0 | 16.1 | 17.0 | 18.2 | 19.4 | 20.6 | 22.0 |
| Temperature °C | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
| ea mbar | 23.4 | 24.9 | 26.4 | 28.1 | 29.8 | 31.7 | 33.6 | 35.7 | 37.8 | 40.1 | 42.4 | 44.9 | 47.6 | 50.3 | 53.2 | 56.2 | 59.4 | 62.8 | 66.3 | 69.9 |
Table 3.II: Extra-terrestrial Radiation (Ra) expressed in equivalent evaporation in mm/day
| Northern Hemisphere | Southern Hemisphere | |||||||||||||||||||||||
| Jan | Feb | Mar | Apr | May | June | July | Aug | Sept | Oct | Nov | Dec | Lat | Jan | Feb | Mar | Apr | May | June | July | Aug | Sept | Oct | Nov | Dec |
| -6.4 | 8.6 | 11.4 | 14.3 | 16.4 | 17.3 | 16.7 | 15.2 | 12.5 | 9.6 | 7.0 | 5.7 | 40° | 17.9 | 15.7 | 12.5 | 9.2 | 6.6 | 5.3 | 5.9 | 7.9 | 11.0 | 14.2 | 16.9 | 18.3 |
| 6.9 | 9.0 | 11.8 | 14.5 | 16.4 | 17.2 | 16.7 | 15.3 | 12.8 | 10.0 | 7.5 | 6.1 | 38 | 17.9 | 15.8 | 12.8 | 9.6 | 7.1 | 5.8 | 6.3 | 8.3 | 11.4 | 14.4 | 17.0 | 18.3 |
| 7.4 | 9.4 | 12.1 | 14.7 | 16.4 | 17.2 | 16.7 | 15.4 | 13.1 | 10.6 | 8.0 | 6.6 | 36 | 17.9 | 16.0 | 13.2 | 10.1 | 7.5 | 6.3 | 6.8 | 8.8 | 11.7 | 14.6 | 17.0 | 18.2 |
| 7.9 | 9.8 | 12.4 | 14.8 | 16.5 | 17.1 | 16.8 | 15.5 | 13.4 | 10.8 | 8.5 | 7.2 | 34 | 17.8 | 16.1 | 13.5 | 10.5 | 8.0 | 6.8 | 7.2 | 9.2 | 12.0 | 14.9 | 17.1 | 18.2 |
| 8.3 | 10.2 | 12.8 | 15.0 | 16.5 | 17.0 | 16.8 | 15.6 | 13.6 | 11.2 | 9.0 | 7.8 | 32 | 17.8 | 16.2 | 13.8 | 10.9 | 8.5 | 7.3 | 7.7 | 9.6 | 12.4 | 15.1 | 17.2 | 18.1 |
| 8.8 | 10.7 | 13.1 | 15.2 | 16.5 | 17.0 | 16.8 | 15.7 | 13.9 | 11.6 | 9.5 | 8.3 | 30 | 17.8 | 16.4 | 14.0 | 11.3 | 8.9 | 7.8 | 8.1 | 10.1 | 12.7 | 15.3 | 17.3 | 18.1 |
| 9.3 | 11.1 | 13.4 | 15.3 | 16.5 | 16.8 | 16.7 | 15.7 | 14.1 | 12.0 | 9.9 | 8.8 | 28 | 17.7 | 16.4 | 14.3 | 11.6 | 9.3 | 8.2 | 8.6 | 10.4 | 13.0 | 15.4 | 17.2 | 17.9 |
| 9.8 | 11.5 | 13.7 | 15.3 | 16.4 | 16.7 | 16.6 | 15.7 | 14.3 | 12.3 | 10.3 | 9.3 | 26 | 17.6 | 16.4 | 14.4 | 12.0 | 9.7 | 8.7 | 9.1 | 10.9 | 13.2 | 15.5 | 17.2 | 17.8 |
| 10.2 | 11.9 | 13.9 | 15.4 | 16.4 | 16.6 | 16.5 | 15.8 | 14.5 | 12.6 | 10.7 | 9.7 | 24 | 17.5 | 16.5 | 14.6 | 12.3 | 10.2 | 9.1 | 9.5 | 11.2 | 13.4 | 15.6 | 17.1 | 17.7 |
| 10.7 | 12.3 | 14.2 | 15.5 | 16.3 | 16.4 | 16.4 | 15.8 | 14.6 | 13.0 | 11.1 | 10.2 | 22 | 17.4 | 16.5 | 14.8 | 12.6 | 10.6 | 9.6 | 10.0 | 11.6 | 13.7 | 15.7 | 17.0 | 17.5 |
| 11.2 | 12.7 | 14.4 | 15.6 | 16.3 | 16.4 | 16.3 | 15.9 | 14.8 | 13.3 | 11.6 | 10.7 | 20 | 17.3 | 16.5 | 15.0 | 13.0 | 11.0 | 10.0 | 10.4 | 12.0 | 13.9 | 15.8 | 17.0 | 17.4 |
| 11.6 | 13.0 | 14.6 | 15.6 | 16.1 | 16.1 | 16.1 | 15.8 | 14.9 | 13.6 | 12.0 | 11.1 | 18 | 17.1 | 16.5 | 15.1 | 13.2 | 11.4 | 10.4 | 10.8 | 12.3 | 14.1 | 15.8 | 16.8 | 17.1 |
| 12.0 | 13.3 | 14.7 | 15.6 | 16.0 | 15.9 | 15.9 | 15.7 | 15.0 | 13.9 | 12.4 | 11.6 | 16 | 16.9 | 16.4 | 15.2 | 13.5 | 11.7 | 10.8 | 11.2 | 12.6 | 14.3 | 15.8 | 16.7 | 16.8 |
| 12.4 | 13.6 | 14.9 | 15.7 | 15.8 | 15.7 | 15.7 | 15.7 | 15.1 | 14.1 | 12.8 | 12.0 | 14 | 16.7 | 16.4 | 15.3 | 13.7 | 12.1 | 11.2 | 11.6 | 12.9 | 14.5 | 15.8 | 16.5 | 16.6 |
| 12.8 | 13.9 | 15.1 | 15.7 | 15.7 | 15.5 | 15.5 | 15.6 | 15.2 | 14.4 | 13.3 | 12.5 | 12 | 16.6 | 16.3 | 15.4 | 14.0 | 12.5 | 11.6 | 12.0 | 13.2 | 14.7 | 15.8 | 16.4 | 16.5 |
| 13.2 | 14.2 | 15.3 | 15.7 | 15.5 | 15.3 | 15.3 | 15.5 | 15.3 | 14.7 | 13.6 | 12.9 | 10 | 16.4 | 16.3 | 15.5 | 14.2 | 12.8 | 12.0 | 12.4 | 13.5 | 14.8 | 15.9 | 16.2 | 16.2 |
| 13.6 | 14.5 | 15.3 | 15.6 | 15.3 | 15.0 | 15.1 | 15.4 | 15.3 | 14.8 | 13.9 | 13.3 | 8 | 16.1 | 16.1 | 15.5 | 14.4 | 13.1 | 12.4 | 12.7 | 13.7 | 14.9 | 15.8 | 16.0 | 16.0 |
| 13.9 | 14.8 | 15.4 | 15.4 | 15.1 | 14.7 | 14.9 | 15.2 | 15.3 | 15.0 | 14.2 | 13.7 | 6 | 15.8 | 16.0 | 15.6 | 14.7 | 13.4 | 12.8 | 13.1 | 14.0 | 15.0 | 15.7 | 15.8 | 15.7 |
| 14.3 | 15.0 | 15.5 | 15.5 | 14.9 | 14.4 | 14.6 | 15.1 | 15.3 | 15.1 | 14.5 | 14.1 | 4 | 15.5 | 15.8 | 15.6 | 14.9 | 13.8 | 13.2 | 13.4 | 14.3 | 15.1 | 15.3 | 15.5 | 15.4 |
| 14.7 | 15.3 | 15.6 | 15.3 | 14.6 | 14.2 | 14.3 | 14.9 | 15.3 | 15.3 | 14.8 | 14.4 | 2 | 15.3 | 15.7 | 15.7 | 15.1 | 14.1 | 13.5 | 13.7 | 14.5 | 15.2 | 15.5 | 15.3 | 15.1 |
| 15.0 | 15.5 | 15.7 | 15.3 | 14.4 | 13.9 | 14.1 | 14.8 | 15.3 | 14.4 | 15.1 | 14.8 | 0 | 15.0 | 15.5 | 15.7 | 15.3 | 14.4 | 13.9 | 14.1 | 14.8 | 15.3 | 15.4 | 15.1 | 14.8 |
Table 3.IV: Mean Daily Duration of Maximum Possible Sunshine Hours (N) for Different Months and Latitudes
| Northern Latitudes | Jan | Feb | Mar | Apr | May | June | July | Aug | Sept | Oct | Nov | Dec |
| Southern Latitudes | July | Aug | Sept | Oct | Nov | Dec | Jan | Feb | Mar | Apr | May | June |
| 40 | 9.6 | 10.7 | 11.9 | 13.3 | 14.4 | 15.0 | 14.7 | 13.7 | 12.5 | 11.2 | 10.0 | 9.3 |
| 35 | 10.1 | 11.0 | 11.9 | 13.1 | 14.0 | 14.5 | 14.3 | 13.5 | 12.4 | 11.3 | 10.3 | 9.8 |
| 30 | 10.4 | 11.1 | 12.0 | 12.9 | 13.6 | 14.0 | 13.9 | 13.2 | 12.4 | 11.5 | 10.6 | 10.2 |
| 25 | 10.7 | 11.3 | 12.0 | 12.7 | 13.3 | 13.7 | 13.5 | 13.0 | 12.3 | 11.6 | 10.9 | 10.6 |
| 20 | 11.0 | 11.5 | 12.0 | 12.6 | 13.1 | 13.3 | 13.2 | 12.8 | 12.3 | 11.7 | 11.2 | 10.9 |
| 15 | 11.3 | 11.6 | 12.0 | 12.5 | 12.8 | 13.0 | 12.9 | 12.6 | 12.2 | 11.8 | 11.4 | 11.2 |
| 10 | 11.6 | 11.8 | 12.0 | 12.3 | 12.6 | 12.7 | 12.6 | 12.4 | 12.1 | 11.8 | 11.6 | 11.5 |
| 5 | 11.8 | 11.9 | 12.0 | 12.2 | 12.3 | 12.4 | 12.3 | 12.3 | 12.1 | 12.0 | 11.9 | 11.8 |
| 0 | 12.0 | 12.0 | 12.0 | 12.0 | 12.0 | 12.0 | 12.0 | 12.0 | 12.0 | 12.0 | 12.0 | 12.0 |
Table 3.IV: Effect of Temperature f(T) on Longwave Radiation (Rnl)
| T°C | 0 | 2 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36.6 | |
| f(T)= TK4 | 11.0 | 11.4 | 11.7 | 12.0 | 12.4 | 12.7 | 13.1 | 13.5 | 13.8 | 14.2 | 14.6 | 15.0 | 15.4 | 15.9 | 16.3 | 16.7 | 17.2 | 17.7 | 18.1 |
Table 3.V: Effect of Vapour Pressure f(ed) on Longwave Radiation (Rnl)
| ed mbar | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| f(ed)=0.34 - 0.044 ed | 0.23 | .22 | .20 | .19 | .18 | .16 | .15 | .14 | .13 | .12 | .12 | .11 | .10 | .09 | .08 | .08 | .07 | .06 |
Table 3.VI: Effect of the Ratio Actual and Maximum Bright Sunshine Hours f(n/N) on Longwave Radiation (Rnl)
| n/N | 0 | .05 | .1 | .15 | .2 | .25 | .3 | .35 | .4 | .45 | .5 | .55 | .6 | .65 | .7 | .75 | .8 | .85 | .9 | .95 | 1.0 |
| f(n/N)= 0.1+0.9n/N | 0.10 | .15 | .19 | .24 | .28 | .33 | .37 | .42 | .46 | .51 | .55 | .60 | .64 | .69 | .73 | .78 | .82 | .87 | .91 | .96 | 1.0 |
Table 3.VII: Values of Weighting Factor (W) for the Effect of Radiation on ETo at Different Temperatures and Altitudes
| Temperature °C | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| Wat altitude m-0 | 0.43 | .46 | .49 | .52 | .55 | .58 | .61 | .64 | .66 | .69 | .71 | .73 | .75 | .77 | .78 | .80 | .82 | .83 | .84 | .85 |
| 500 | .45 | .48 | .51 | .54 | .57 | .60 | .62 | .65 | .67 | .70 | .72 | .74 | .76 | .78 | .79 | .81 | .82 | .84 | .85 | .86 |
| 1 000 | .46 | .49 | .52 | .55 | .58 | .61 | .64 | .66 | .69 | .71 | .73 | .75 | .77 | .79 | .80 | .82 | .83 | .85 | .86 | .87 |
| 12 000 | .49 | .52 | .55 | .58 | .61 | .64 | .66 | .69 | .71 | .73 | .75 | .77 | .79 | .81 | .82 | .84 | .85 | .86 | .87 | .88 |
| 3 000 | .52 | .55 | .58 | .61 | .64 | .66 | .69 | .71 | .73 | .75 | .77 | .79 | .81 | .82 | .84 | .85 | .86 | .88 | .89 |
Table 3.VIII: Adjustment Factor (c) in Presented Penman Equation
| R Hmax = 30% | R Hmax = 60% | R Hmax = 90% | ||||||||||
| Rs mm/day | 3 | 6 | 9 | 12 | 3 | 6 | 9 | 12 | 3 | 6 | 9 | 12 |
| U day m/sec | U day/U night = 4.0 | |||||||||||
| 0 | .86 | .90 | 1.00 | 1.00 | .96 | .98 | 1.05 | 1.05 | 1.02 | 1.06 | 1.10 | 1.10 |
| 3 | .79 | .84 | .92 | .97 | .92 | 1.00 | 1.11 | 1.19 | .99 | 1.10 | 1.27 | 1.32 |
| 6 | .68 | .77 | .87 | .93 | .85 | .96 | 1.11 | 1.19 | .94 | 1.10 | 1.26 | 1.33 |
| 9 | .55 | .65 | .78 | .90 | .76 | .88 | 1.02 | 1.14 | .88 | 1.01 | 1.16 | 1.27 |
| U day/U night = 3.0 | ||||||||||||
| 0 | .86 | .90 | 1.00 | 1.00 | .96 | .98 | 1.05 | 1.05 | 1.02 | 1.06 | 1.10 | 1.10 |
| 3 | .76 | .81 | .88 | .94 | .87 | .96 | 1.06 | 1.12 | .94 | 1.04 | 1.18 | 1.28 |
| 6 | .61 | .68 | .81 | .88 | .77 | .88 | 1.02 | 1.10 | .86 | 1.01 | 1.15 | 1.22 |
| 9 | .46 | .56 | .72 | .82 | .67 | .79 | .88 | 1.05 | .78 | .92 | 1.06 | 1.18 |
| U day/U night = 2.0 | ||||||||||||
| 0 | .86 | .90 | 1.00 | 1.00 | .96 | .98 | 1.05 | 1.05 | 1.02 | 1.06 | 1.10 | 1.10 |
| 3 | .69 | .76 | .85 | .92 | .83 | .90 | .99 | 1.05 | .89 | .98 | 1.10 | 1.14 |
| 6 | .53 | .61 | .74 | .84 | .70 | .80 | .94 | 1.02 | .79 | .92 | 1.05 | 1.12 |
| 9 | .37 | .48 | .65 | .76 | .59 | .70 | .84 | .95 | .71 | .81 | .96 | 1.06 |
| U day/U night = 1.0 | ||||||||||||
| 0 | .86 | .90 | 1.00 | 1.00 | .96 | .98 | 1.05 | 1.05 | 1.02 | 1.06 | 1.10 | 1.10 |
| 3 | .64 | .71 | .82 | .89 | .78 | .86 | .94 | .99 | .85 | .92 | 1.01 | 1.05 |
| 6 | .43 | .53 | .68 | .79 | .62 | .70 | .84 | .93 | .72 | .82 | .95 | 1.00 |
| 9 | .27 | .41 | .59 | .70 | .50 | .60 | .75 | .87 | .62 | .72 | .87 | .96 |