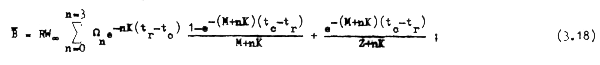Uno de los aspectos que caracterizan a las poblaciones es que están constituidas por individuos de varias edades diferentes. Tantas, que al agrupar a todos los individuos de acuerdo con el año de su nacimiento o de acuerdo con el año en que se integraron a la población podemos encontrar tantos grupos de edad como años pueda sobrevivir la especie. Así, si por ejemplo tenemos una especie cuya longevidad o edad máxima es tλ = 6 años, es de esperar que la población de esta especie esté constituida hasta por seis grupos de edad, cada uno de los cuales corresponderá a una clase anual diferente. Ya en el capítulo anterior hemos seguido a una sola clase anual en su paso por la vida y hemos podido apreciar los cambios que experimenta desde que aparece hasta que se extingue. Trataremos ahora de hacer el mismo seguimiento pero esta vez a nivel de toda la población.
Resulta explicable que las clases anuales tengan una existencia relativamente corta ya que la duración de su vida está limitada; en primera instancia por la mortalidad que la va mermando paulatinamente hasta extinguirla y, en última instancia, por la longevidad o edad máxima (tλ) que es característica para cada especie y a la cual las clases anuales no pueden teóricamente sobrevivir.
La población en cambio es un ente perdurable, compuesto en todo momento por una o más clases anuales que avanzan paralelamente por la vida sucediéndose unas a otras de forma que así como cada año hay una clase anual ya vieja que se extingue y desaparece, cada año también aparece una nueva clase anual, compuesta por individuos jóvenes. La población puede entonces considerarse como un ente por el cual pasan en sucesión las clases anuales portando cierta cantidad de individuos que tienen características propias a su talla o edad promedio.
Es así como el tamaño y la estructura de la población en todo momento es el resultado del tamaño y las características de cada una de las clases anuales existentes en ese instante. Por ejemplo, si en el año 1970 tomamos a la población de peces de las fig. 3.1 y 3.2 después del ingreso de la clase anual correspondiente a ese año, encontraremos que la población en dicho año será el resultado de la suma de los individuos de la clase anual de 1970, que recién han ingresado, más, los individuos sobrevivientes de la clase anual de 1969 que ya han cumplido t = 1 año de edad, más los sobrevivientes de la clase anual de 1968, que ya tienen t = 2 años de edad, más los sobrevivientes de la clase anual de 1967, que tienen t = 3 años, más los sobrevivientes de la clase anual de 1966 que ya tienen t = 4 años y así sucesivamente, hasta llegar a la última clase anual sobreviviente o hasta llegar a la clase anual que esté por alcanzar la edad máxima t = tλ. De acuerdo con ésto, la estructura de la población en el año 1970 (P70) se puede representar mediante la expresión:
P(70) = N 0 (70) + N 0 (69) e -Z + N 0 (68) e -Z(2) + … + N 0 (70-tλ) e -Z(tλ);
Como por definición ningún individuo puede sobrevivir a la edad máxima tλ, ya sea que tλ tome un valor real o que tome un valor infinitamente grande, se debe cumplir que:
Ntλ = No e -Ztλ = O ;
Con lo cual la expresión anterior puede generalizarse suprimiendo el último término, de forma que:
Pi = N 0 (i) + N 0 (i - 1) e -Z + N 0 (i - 2) e -Z(2) + … + N 0 (i - tλ + 1) e -Z(tλ - 1);
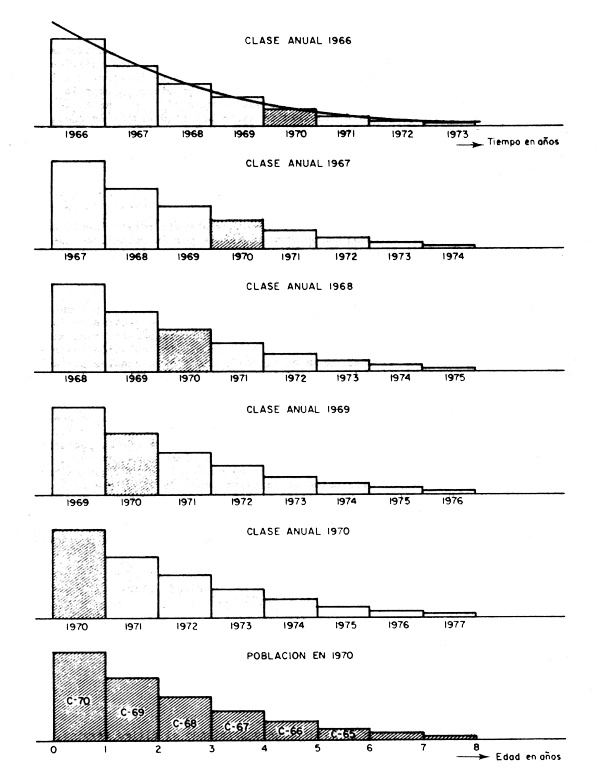
Figura 3.1 Equivalencia entre la estructura por edades de las clases anuales a través del tiempo y la estructura por edades de la población en un momento dado bajo condiciones constantes
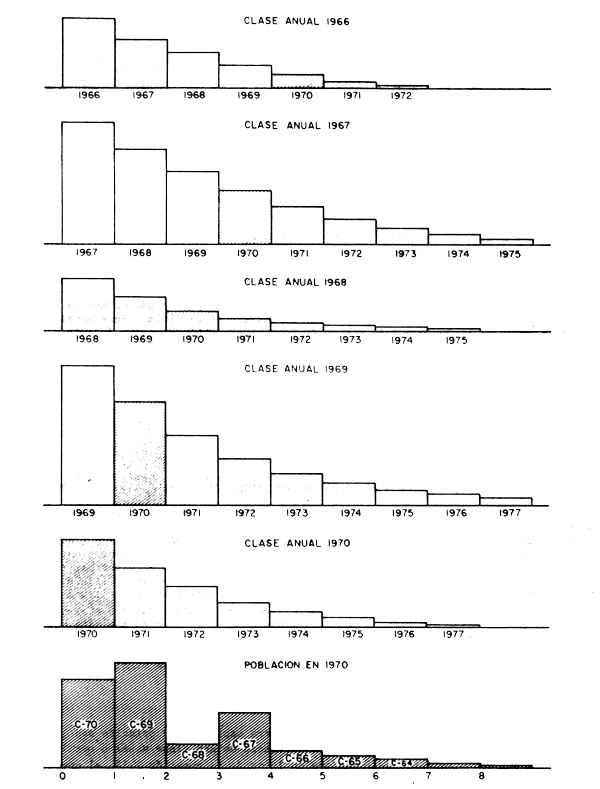
Figura 3.2 Equivalencia entre la estructura por edades de las clases anuales a través del tiempo y la estructura por edades de la población enun momento dado, bajo condiciones variables
o también:

donde:
Pi = población en número en el año i, inmediatamente después del ingreso de una nueva clase anual;
No = número inicial de individuos de cada clase anual;
t = tiempo;
tλ = longevidad o edad máxima;
Z = coeficiente instantáneo de mortalidad total.
Ahora, si queremos determinar el tamaño de la población después de que ha transcurrido una fracción φ de la unidad de tiempo desde el ingreso de la última clase anual, tendremos que considerar el hecho de que la población debe haber estado expuesta durante dicha fracción de tiempo al efecto descendente de la mortalidad, y en este caso:
Piφ = Pi e -Z(φ)
y por lo tanto;

donde φ representa una fracción de la unidad de tiempo que en este caso es un año.
En la vida real resulta sumamente difícil conocer la magnitud o tamaño de las clases anuales antes del reclutamiento ya que, como los pre-reclutas no están accesibles a la pesquería, sus integrantes no pueden ser encontrados ni cuantificados hasta que no hayan pasado a formar parte de la población explotable. Razón por la cual es más conveniente tomar el número de individuos que completan el reclutamiento, es decir la magnitud del reclutamiento (R), como punto de partida para seguir la historia de las clases anuales en lugar de tomar el número inicial de individuos (No), que en este caso corresponde a una edad t = 0 donde los peces pueden ser muy numerosos pero tienen un tamaño y un peso promedio insignificante, además de estar expuestos a una mortalidad natural (M') mucho más alta que la mortalidad natural (M) a la cual están expuestos los estadios posreclutas.
Si consideramos que el reclutamiento ocurre a una edad tr la magnitud del reclutamiento (R) será:
R = No e-M'tr) ;
donde M'>>M, y si asumimos que la edad a la primera captura (tc) coincide con la edad del reclutamiento (tr) podemos expresar la sobrevivencia de una clase anual a partir del número o magnitud del reclutamiento, de forma que en lugar de la ecuación 2.11, el número de individuos sobrevivientes de una clase anual a cualquier edad t posterior al reclutamiento será:
| Nt = Re -Z(t - tr); | (3.3) |
Normalmente la edad a la primera captura (tc) y la edad del reclutamiento (tr) coinciden, pero hay casos en que las regulaciones pesqueras o el bajo interés por capturar a los peces recién reclutados (por ser más pequeños) hacen que la edad a la primera captura sea mayor que la edad del reclutamiento. En este caso (cuando tc > tr) la ecuación anterior debe escribirse:
| Nt = R e -M (to - tr) e -Z(t - to); | (3.3a) |
En el primer caso (cuando tr = tc) la ecuación 3.2 puede escribirse haciendo:
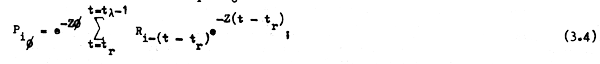
y si tenemos condiciones ideales y el reclutamiento es constante, es decir, si:
R = Ri = Ri - 1 = Ri - 2 = … = Ri - n;
la población explotable en cualquier año, una fracción de tiempo φ después de haberse producido el último reclutamiento, será:

y por ende, la población existente inmediatamente después de haberse producido el reclutamiento (cuando la fracción de tiempo es φ = 0) será:

lo que como veremos a continuación, es igual a la suma de los grupos de edad existentes a través del tiempo en una sola clase anual.
Efectivamente, si entre las edades tr y tλ seguimos a todos los individuos de una misma clase anual registrándolos y sumándolos independientemente cada vez que crecen a una edad mayor, podemos modificar la ecuación 3.3 que describe la sobrevivencia de una sola clase anual en función al reclutamiento de forma que:

Comparando esta ecuación con la ecuación 3.6 tenemos que:

de donde podemos concluir que cuando el reclutamiento es constante, y siempre que la mortalidad sea también constante, la población en un momento dado tiene el mismo tamaño y la misma estructura que una sola clase anual a lo largo de toda su existencia. Hecho que se ha tratado de ilustrar en el ejemplo de la fig. 3.1, y que en la práctica permite que la estructura de la población en un momento dado pueda ser averiguada si se conoce la historia de una sola clase anual, y viceversa, es decir, si esta condición se oumple, es posible también conocer la historia de una clase anual (incluyendo la sobrevivencia y el crecimiento) a partir de la estructura que tiene la población en un momento dado.
Esta correspondencia tan singular entre lo que ocurre con la población en un momento dado y lo que ocurre con cada clase anual a lo largo de su existencia sólo se da bajo condiciones ideales donde la mortalidad y el reclutamiento son constantes. Una situación muy diferente, aunque no por ello menos frecuente, se da cuando el reclutamiento es variable (fig. 3.2). En cuyo caso las ecuaciones 3.1, 3.2, 3.3 y 3.4 así como sus conceptos previos siguen teniendo plena validez, no así las que se refieren a las ecuaciones 3.5, 3.6 y 3.7 que sólo son válidas bajo condiciones ideales.
Si analizamos la ecuación 3.6 encontraremos que sus términos corresponden al desarrollo de una serie geométrica convergente, donde:
PO = R + Re-Z(1) + Re-Z(2) + Re-Z(3) + … + Re-Z(tλ - tr - 1) ;
cuya suma es:
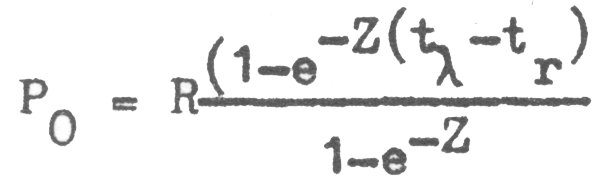
y, ya sea que (tλ - tr) tienda a hacerse infinitamente grande o que por definición hagamos que la tasa de sobrevivencia a la edad máxima (e-Ztλ) se haga infinitamente pequeña, tenemos que el limite de la expresión anterior es:

que expresa que bajo condiciones ideales de equilibrio la población en número (P0) existente inmediatamente después de haberse producido el reclutamiento es en cualquier año igual a la magnitud del reclutamiento (R) dividida entre la tasa anual de mortalidad total, que es A = 1-e-Z.
Lógicamente, luego de haberse producido el último reclutamiento la población se irá reduciendo paulatinamente debido al efecto de la mortalidad, hasta que ocurra un nuevo reclutamientoal año siguiente (fig. 3.3). De esta forma el número de individuos en la población luego de haber transcurrido una fracción de tiempo φ entre un reclutamiento y otro será:

donde φ es una fracción cualquiera de la unidad de tiempo existente, que en este caso es t = 1 año.
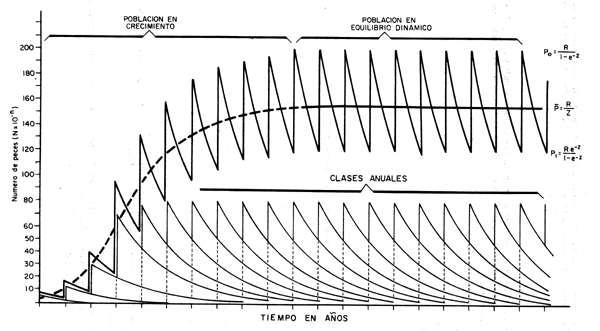
Figura 3.3 Fluctuaciones en la población en número en relación a la mortalidad (Z) y al reclutamiento (R) condiciones de equilibrio y parámetros constantes
La población llegará a su nivel mínimo inmediatamente antes de producirse un nuevo reclutamiento(cuando la fracción de tiempo φ se aproxima a 1) con lo que la ecuación 3.9 se hace:
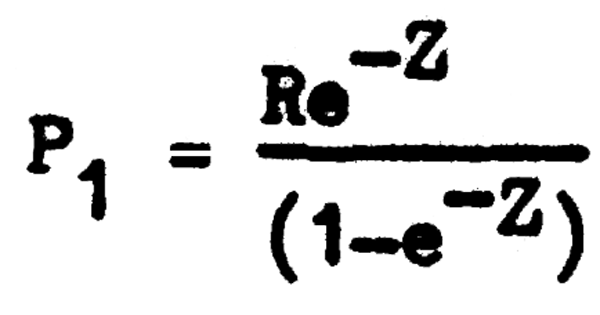
De esta forma la población fluctuará constantemente entre los valores P0 y P1 pasando por todos los valores posibles de Pφ, por lo cual, si queremos conocer el tamaño promedio de la población, tendremos que hacer:
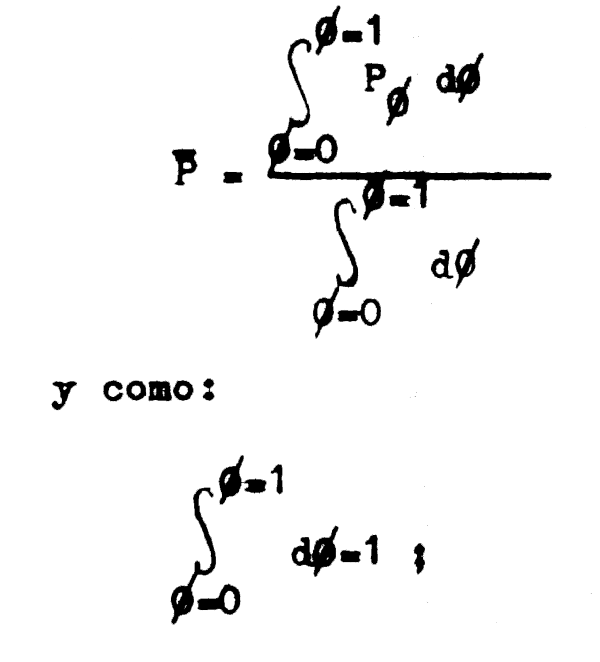
reemplazando Pφ por el valor de la ecuación 3.9 tenemos que:

que expresa que bajo condiciones ideales de equilibrio la población promedio es igual a reclutamiento entre la tasa instantánea de mortalidad total.
En el capítulo anterior (ecuación 2.24) hemos llegado a establecer que el peso o biomasa total de una clase anual a cualquier edad t es:
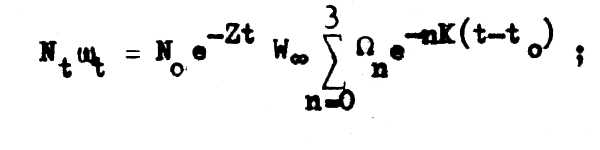
pero como nuestro interés en la biomasa de las poblaciones de peces explotables comienza cuando sus integrantes han entrado en la fase explotable, podemos expresar la ecuación anterioren función al reclutamiento (R), que en la práctica es más fácil de determinar que N0 de forma que:
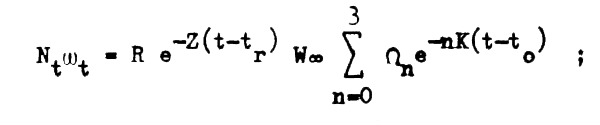
y si sumamos y restamos tr al exponente que está dentro del signo sumatorio la ecuación no se altera:
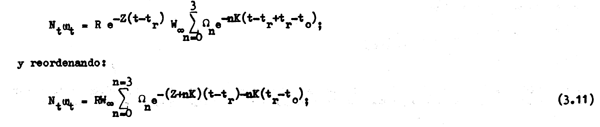
como bajo condiciones ideales de equilibrio la población tiene el mismo tamaño y la misma estructura que una sola clase anual a lo largo de toda su existencia se cumple entonces que el peso o biomasa total de la población explotable al inicio de cualquier período de tiempo o año t, inmediatamente después de haberse producido el reclutamiento será:

y, luego de haber transcurrido una fracción de tiempo φ entre un año y otro, o entre un reclutamientoy otro, la biomasa de la población en cualquier instante t + φ será:
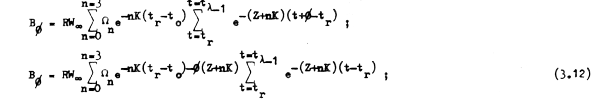
dende la expresión de la segunda sumatoria desarrolla una serie geomótrica convergente:
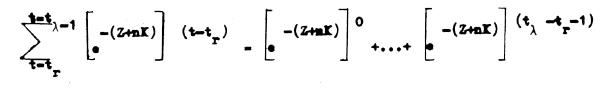
cuya suma es:
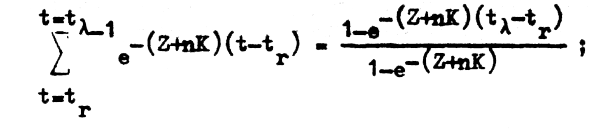
si hallamos el límite cuando tλ tiende a infinito, o si de acuerdo con la definición de tλ hacemos que la tasa de sobrevivencia sea igual a cero de forma que:
S = e -tλ = o ;
la expresión anterior se hace:
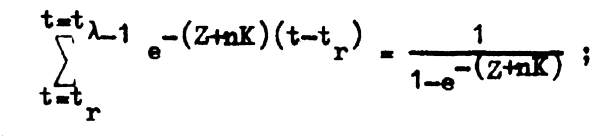
y, reemplazando en la ecuación 3.12, tenemos que en cualquier instante o fracción de tiempo φ de un año cualquiera, la biomasa total de la población bajo condiciones de equilibrio es:

Por último, para hallar el peso o la biomasa total promedio de la población en cualquier tiempo o año t, tenemos que integrar la ecuación anterior entre los límites de la fracción de tiempo φ = 0 y φ = 1, de forma que:

que nos permite expresar la biomasa total promedio de la población explotable en función a la tasa de crecimiento y a la mortalidad total en cualquier año, siempre que se den condicionesideales de equilibrio.
Nótese que si las primeras capturas se comenzaran a realizar algún tiempo después de haberse producido el reclutamiento, es decir si tc es mayor que tr, habría que considerar la expresión 3.3a en lugar de la 3.3 en todas las ecuaciones anteriores, con lo cual la poblaciónen número en el momento φ de cualquier año (ecuación 3.9) será:
| Pφ = R e -M (tc - tr) e -Zφ | (3.15) |
el número promedio de peces en la población (ecuación 3.10) se expresará por:

la población en peso o biomasa en el momento φ de cualquier año (ecuación 3.13) se reempla– zará por la expresión :
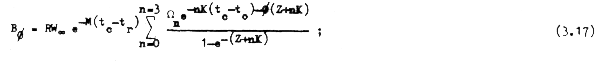
y por último la biomasa promedio en cada año sería: