8.1 INPUT-OUTPUT OR RESPONSE RELATIONSHIPS
8.2 OPTIMIZATION OF A SINGLE-VARIABLE INPUT RESPONSE PROCESS
8.3 OPTIMIZATION OF MULTI-VARIABLE INPUT RESPONSE PROCESSES
8.4 DATA SOURCES FOR RESPONSE ANALYSIS
8.5 DIFFICULTIES IN RESPONSE ANALYSIS
8.6 REFERENCES
'But for the law of diminishing returns, it would be possible to grow all of the world's grain needs in a bucket.'Earl O. Heady (1916 - 1987)
From Chapter 7, the two main weaknesses that may be uncovered by farm management analysis in diagnostic Mode are, first, those arising from the use of suboptimal levels of resources within individual activities and, second, inefficient combinations of activities. Analogously, in analysis in prescriptive Mode (system planning), the two main tasks of the farm management analyst are to define the best levels of resources to use in potential future activities and the best mix of such activities. Optimization of the activity mix is discussed in Chapter 9. This chapter is concerned with the first problem, i.e., determining the best levels of resources within activities.
For either restructuring weak activities or formulating new ones, the problem reduces to constructing an input-output activity budget. However, unlike a budget which simply describes the actual resource composition of a past or existing activity, or what a farmer has done, this planning or adjustment budget now specifies what the farmer should do in terms of allocating resources to the activity.
Specifying the 'best' levels of resources to use in respective activities will usually present few problems. Farmers will base their estimates of the best seeding rates, irrigation frequencies, fertilizer rates etc. on their own experience or village practice or local lore or, in a few cases, on reference to farm records. For new inputs with which they are not familiar, the estimates might be based on the (sometimes dubious) advice of fertilizer or agricide agents or on the more objective recommendations of extension workers.
These sources of data will usually be a sufficient basis for making at least reasonable estimates of the best levels of resources to use in individual activities. However, in a few cases it will be necessary to take a more formal approach to determine the best levels of resource use in an activity, viz.:
(i) When the cost of an input and/or the value of its effect on output is economically significant, i.e., sufficiently great as to warrant the cost of obtaining more precise information.(ii) When the likely effect of an input is quite unknown and the farmer (or more likely an analyst or extension worker on behalf of a group of farmers) sees the need for a small-scale field trial before deciding on the use of the input.
(iii) If sharp or significant changes occur in what have been stable input unit costs and/or output prices, resulting in the likelihood that past levels of resource use should now be changed.
(iv) When entirely new activities or technologies are introduced to an area so that new activity budgets must be constructed.
(v) On mono-crop farms and estates where more intensive effort will routinely be devoted to input-output relationships which, for these same activities on small mixed farms, might be of only marginal interest and where rough approximations are good enough.
In these situations the more formal methods of response analysis might be required to determine optimal input levels. An introduction to such methods is given here. A more extensive introduction is provided by Amir and Knipscheer (1989, Ch. 3) and Dillon and Hardaker (1993, Ch. 7) while a relatively comprehensive formal presentation is to be found in, e.g., Beattie and Taylor (1985), Debertin (1986), Dillon and Anderson (1990), Doll and Orazem (1984, Chs 2, 3, 4 and 5) and Rae (1977, Chs 2, 3 and 4). A variety of applications of response analysis is to be found in Heady and Dillon (1961), Heady and Bhide (1984) and Hexem and Heady (1978).
Agricultural input-output relationships are, in themselves, of a physical nature. Their manipulation and (so far as possible) control by the farmer so as to achieve his or her goals, however, implies that these physical relationships have to be evaluated in value terms as determined by the market price or opportunity cost of outputs and inputs.
Physical relationships in response analysis
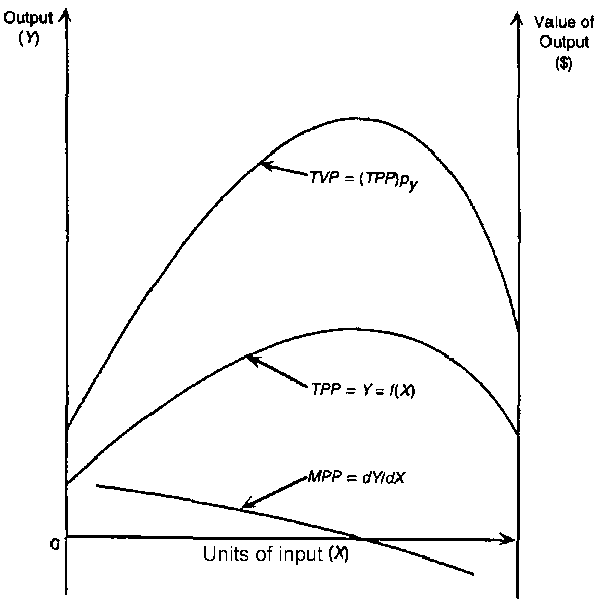
An illustration of the physical response curve or production function showing total physical product (TPP) for a single input/single output situation is given in Figure 8.1. Note that, by convention and for convenience, the symbols Y and X respectively denote both a particular type of output or input and the quantity or level of that output or input per technical unit of production such as per ha of land or other fixed resource (e.g., per animal unit or per tree). Two further physical relationships can be derived from TPP. These are average physical product (APP) and marginal physical product (MPP), both of these being measured on the same technical-unit basis as TPP, These three physical measures are defined as follows:
TPP: Total physical product is the yield or response of output Y in physical units to inputs of X, also in physical units. Thus TPP = Y = f(X) where f(X) denotes the relevant production or response function as outlined in Section 5.1.1.APP: Average physical product is the amount of output achieved per unit of input. Thus APP = TPP/X = Y/X.
MPP: Marginal physical product is the change in TPP in response to a marginal unit change in input. Thus MPP = D TPP/D X = dTPP/dX = dY/dX where the symbol D (.) denotes a small increment in (.) and dY/dX is the first derivative of Y = f(X).
While the TPP and MPP curves are illustrated in Figure 8.1, the APP curve is not shown. However, note that APP for any point on the TPP curve is given by the slope of a radius from the origin to the point on the TPP curve since such a radius has slope of Y/X = APP.
As drawn in Figure 8.1, the TPP curve reflects the law of diminishing returns. This is because, as additional variable input X is applied in conjunction with the amount of fixed resource being used. MPP declines. Initially, while TPP continues to increase, MPP is positive. Eventually, however, TPP reaches a maximum and then declines absolutely at which stage MPP becomes increasingly negative.
FIGURE 8.1 - Total Physical Product (TPP), Marginal Physical Product (MPP) and Total Value Product (TVP) per Technical Unit for a Single-variable Production Function Y = f(X)
Value relationships in response analysis
Since optimization is to be achieved in economic (here financial) terms, it is necessary to convert the above physical relationships to a value basis per technical unit. This is done simply by multiplying TPP, APP and MPP by the unit price py of the output to obtain:
|
Total value product: |
TVP = (TPP)py |
|
Average value product: |
AVP = (APP)py |
|
Marginal value product: |
MVP = (MPP)py |
Of these value relationships, only TVP is shown in Figure 8.1. In fact, for the economic analysis of response, only the TVP and MVP relationships are needed; the average relationships APP and AVP are not further discussed except to note that, on the basis of purely physical efficiency, the amount of input used should never be less than the level at which its MPP equals its APP so that its APP is decreasing, not increasing. Likewise, and again on purely physical grounds, the amount of input should never exceed the level at which its MPP becomes negative. Thus the use of an input should always lie within the range where its MPP satisfies the condition APP ³ MPP ³ 0. Within this range, the optimal level of the input will be determined by the relative price ratio px/py as outlined in Section 8.2 below.
It should also be noted that in making the conversion from physical to value terms it is necessary to assume that output price py remains constant over all levels of output, i.e., that the unit price which an individual farmer receives for his or her product does not change as he or she produces less or more of it. Constant unit prices usually apply to individual small farmers; they most likely will not apply to farmers in aggregate and to very large producers who produce a sufficient amount of the commodity to influence its market.
On the input side the two relevant parallel relationships are:
Total cost (TC): the cost of inputs required to achieve any specified level of output Y; it is the sum of any relevant fixed cost (FC) (see below) and the variable cost (VC) associated with the variable inputs. This VC is calculated as the number of input units times their unit price, i.e., Xpx for a single input X. (With multiple variable inputs X1, X2...Xn, VC = S Xipi for i = 1 to n.)Marginal cost (MC): is the change in total cost as one more (i.e., marginal) unit of variable input is used. Thus, with px constant, it is simply the unit cost of the variable input.1 Hence, since D FC = 0, for D X = 1:
MC = D TC/AX = D TC = D (FC + VC) = D FC + D VC = D VC = px
1 In production economics theory (as here), marginal cost is defined as cost per unit of input; in cost theory it is defined as cost per additional unit of output.
Here again a parallel assumption is that for any individual small farmer the unit cost of the input is constant regardless of how much of it is purchased. Also, as previously noted (Section 5.3), in addition to fixed costs associated with non-variable or fixed inputs, the cost of such variable inputs as seed, water etc. can also have a 'fixed' component such as the cost of owning/maintaining the machine or facility by which the variable input (seed, water etc.) is applied. However, inclusion of such a fixed component - should it exist - will increase only TC; being a fixed cost and therefore constant, it will not affect MC.
8.2.1 Optimization by partial budgeting
8.2.2 Optimization by graphical methods
8.2.3 Optimization by using the response equation
8.2.4 Optimization by using the profit function
8.2.5 Maximum output vs optimal economic output
8.2.6 Constrained optimization
The objective of resource-use optimization is to maximize the level of net benefit generated by applying a resource to produce an output. Net benefit is simply the difference between total output value and total cost, however measured (Dillon and Anderson 1990, pp. 29-32). In practice, net benefit is usually measured or assessed as money profit. As discussed in Sections 2.1 and 6.1, money profit provides a direct measure of net benefit in the case of market-oriented farms and often a convenient surrogate measure for subsistence-oriented farms. Optimization of simple lower Order Level systems (single- and two-input processes and activities) can be achieved using partial budgets (Chapter 4) or graphs or the mathematical equations on which these latter are based; more complex activity and whole-farm systems usually require a mathematical approach.
The physical input-output data presented in the first two columns of Table 8.1 are from an on-farm trial concerning some animal or crop production process. Note that the data are standardized on the basis of a technical (production) unit of one hectare. The unit cost of the input is Rs 5 and the unit price of output is Rs 0.40. A fixed cost of Rs 6 per ha is associated with the fixed land input and the application of the variable input. First, the base-data input (X) and output (Y) columns are expanded to obtain a partial budget for each level of input showing total value of production (TVP), total cost (TC) and profit (TVP - TC) in the following columns. The optimal level of input use is then found by inspection as that at which profit is a maximum, here Rs 96 resulting from the use of six units of input. This can readily be checked: in the table the use of one less or one more input unit would reduce profit below this maximum level.
TABLE 8.1 - Response Optimization by Partial Budgeting of Profit
|
Trial Data |
TVP |
Costs |
Profit TVP-TC |
|||
|
X |
Y |
FC |
VC |
TC |
||
|
(kg/ha) |
(kg/ha) |
|
(Rs/ha) |
|
||
|
2 |
224 |
89.6 |
6 |
10 |
16 |
73.6 |
|
3 |
264 |
105.6 |
6 |
15 |
21 |
84.6 |
|
4 |
292 |
116.8 |
6 |
20 |
26 |
90.8 |
|
5 |
316 |
126.4 |
6 |
25 |
31 |
95.4 |
|
6 |
330 |
132.0 |
6 |
30 |
36 |
96.0 |
|
7 |
340 |
136.0 |
6 |
35 |
41 |
95.0 |
|
8 |
344 |
137.6 |
6 |
40 |
46 |
91.6 |
|
9 |
340 |
136.0 |
6 |
45 |
51 |
85.0 |
Equivalently, partial budgeting can also be applied using the marginal value relationships, MVP and MC. Here the optimizing rule is to extend input use to that level at which MVP = MC, or alternatively stated, where MVP - MC = 0 (or stated another way, where the use of one less or one more unit of input would result in a decline in profit). These marginal-based partial budgets are shown in Table 8.2 and, as with using the budgets in total terms of Table 8.1, the MVP - MC = 0 condition is achieved with an input of six units approximately - from graphical analysis, the exact optimal level is 6.4 units.
Sometimes the desired physical input-output relationship is available in graphical form. More often, in simple single-input situations, a freehand curve can be sketched through an array of available input-output data such as those of Table 8.2. On the other hand, the relationship might be of such practical economic importance that greater accuracy is warranted in preparing the graph; if so, it must then be derived from an underlying or statistically estimated mathematical response equation or production function as outlined by Dillon and Hardaker (1993, Ch. 7). By whatever means the graph is obtained, its use in resource optimization is usually straightforward. The only practical condition is that the relative prices of the input and the output must be capable of expression as a price ratio, px/py.
TABLE 8.2 - Response Optimization by Partial Budgeting of Marginal Value Relationships
|
Trial Data |
TVP |
MVP |
MC |
MVP - MC |
|
|
X |
Y |
||||
|
(kg/ha) |
(kg/ha) |
(Rs/ha) |
|||
|
2 |
224 |
89.6 |
- |
- |
- |
|
3 |
264 |
105.6 |
16.0 |
5 |
11.0 |
|
4 |
292 |
116.8 |
11.2 |
5 |
6.2 |
|
5 |
316 |
126.4 |
9.6 |
5 |
4.6 |
|
6 |
330 |
132.0 |
5.6 |
5 |
0.6 |
|
7 |
340 |
136.0 |
4.0 |
5 |
-1.0 |
|
8 |
344 |
137.6 |
1.6 |
5 |
-3.4 |
|
9 |
340 |
136.0 |
-1.6 |
5 |
-6.6 |
The graphical approach also makes use of the marginality condition for resource-use optimization, MVP = MC. Noting that MVP is defined as MPP times the unit value or price of the product Y, i.e., MVP = (MPP)py, the optimality condition can be restated as (MPP)py = MC. Noting also that MC is simply the (constant) unit cost of the variable input X, the condition can also be restated as (MPP)py = px or, transposing terms, as MPP = px/py. Since MPP is the rate of change of TPP as X changes, this final relationship states that optimality is achieved by continuing to apply variable input to the process until the resultant rate of change in output (MPP) is equal to the ratio of input unit price px to output unit price py i.e., px/py. The input-output process is then in economic balance in the sense that use of either more or less input would reduce profit. Analogously to the discussion of trade-off between input factors in Section 7.5, this is shown by the fact that MPP = px/py, implies D Y/D X = px/py, or, rearranging, (D Y)py = (D X)px so that the gain (D Y)py, from producing D Y is exactly balanced by the cost (D X)px, of its production. In other words, for maximum profit, the last unit of input must just pay for itself. Because of diminishing returns, prior units of input will have more than paid for themselves; further units of input will not cover their cost.
The operating steps in graphical analysis of response are as follows:
(i) Sketch the physical response curve (TPP of Figure 8.1).(ii) Obtain the price ratio px/py
(iii) Draw a straight-line segment which has a slope ('the rise over the run') equal to the price ratio px/py, and move this towards the TPP curve until it is tangent to (i.e., just touches) this curve.
(iv) At this point of tangency, the TPP curve has the same slope as the px/py price-ratio line. Thus, at the tangency point, the rate of change of Y as X changes, dY/dX, is equal to the price ratio px/py. But from Section 8.1, dY/dX (or dTPP/dX) is the definition of MPP. Therefore, at the tangency point, MPP = px/py, or transposing, (MPP)py = px but (MPP)py is defined as MVP and px is the cost of a marginal unit of input, MC. Thus the tangency point locates the input level at which the optimality condition MVP = MC is met.
(v) Read off from the graph that level of input directly below the tangency point. This is the input level at which MVP = MC, at which profit (TVP - TC) is at a maximum, and where the use of one (marginal) unit less or more of input in the process would result in a profit decrease.
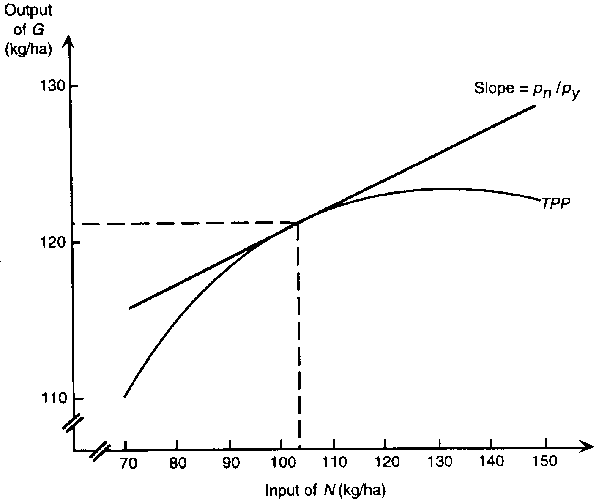
An example of the above procedure is shown in Figure 8.2 for the simple single-input process of applying nitrogen to a grain crop on a per ha basis. The unit price of nitrogen, denoted by pn is assumed to be Rs 0.16 and the unit price of grain, denoted by pg, is Rs 0.90. The pn/pg, ratio is thus 0.16/0.90 = 0.18. The input level per ha at which the price-ratio line having this slope is tangent to the TPP curve is 103 units of nitrogen per ha. At this optimal level of N, the optimal level of output is read off as 121 units of grain per ha.
The use of a response equation to determine the optimal level of a variable input is appropriate if the physical input-output data are available in equation form and/or if a high level of precision is required.
As previously, the optimality condition MVP = MC is used and now applied to the explicit form of a response relationship G = f(N) where G denotes grain output and N denotes nitrogen input. MVP is equal to (MPP)pg, and MPP (i.e., the rate of change of grain output as nitrogen input is marginally changed) is obtained as the first derivative of G with respect to N, i.e., dG/dN. The optimality condition MPP = pn/pg is rewritten as dG/dN = pn/pg.
As an example, suppose the physical response relationship on a per ha basis is
G = 70 + 0.8N - 0.003/N2
and the respective unit prices of nitrogen and grain are Rs 0.16 and Rs 0.90 as previously. The price ratio, as before, is thus 0.18. The optimality condition is then obtained as dG/dN = 0.18, i.e., 0.8 - 0.006N = 0.18. Solving this for N, the optimal level of nitrogen is 103 units per ha. Substituting this value for N in the response equation results in a corresponding output of grain of 70 + 0.8(103) - 0.003(1032) or 121 units per ha.
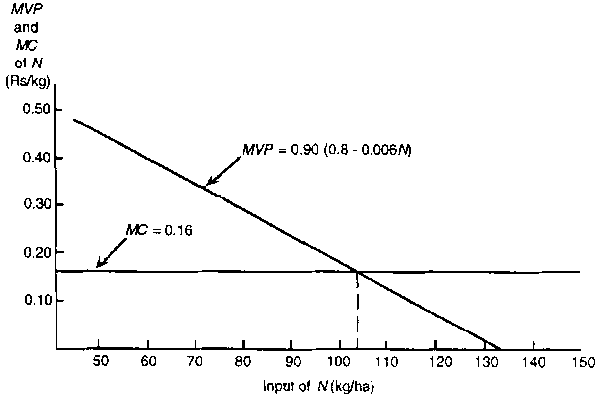
Whichever of the above response-optimization methods - partial budgeting, graphical analysis or response equations - is used, proof that optimality in resource use level is defined by the condition MVP = MC is offered by the graph of Figure 8.3. This diagram shows the graphed values of MVP = (dG/dN)pg = Rs(0.8 - 0.006N)0.90. On the other hand, the horizontal line is the graphed value of MC which is the constant unit cost of N, Rs 0.16. These graphed values are equal, i.e., MVP = MC, at the point of curve intersection. This occurs at an input level of N = 103. 'Proof consists of inspection of the intersection point and observing that with the use of one unit less of input, MVP would be greater than MC and it would pay to add an extra unit of input; with the use of one unit more of input, the (marginal) cost of this last unit of input would be greater than the (marginal) value of product derived from its use. Thus 103 units per ha is the optimal input level.
FIGURE 8.2 - Example of Graphical Analysis of Response
It is often more convenient to approach optimization of resource use in terms of the basic profit equation. Profit was defined previously as total gross return less total cost, i.e., denoting profit by pi, the profit from a response process is
p = TVP-TC
where TC = VC + FC. Total gross return equals TVP which is output times its unit price. FC is here assumed to be Rs 5 per ha. VC is variable input quantity times its unit price. Again using the nitrogen-grain example with pg = Rs 0.90 and pn = Rs 0.16, the equation for profit in Rs per ha is given by:
p = TVP - VC - FC = pgG - pnN - 5 = 0.90(70 + 0.8N - 0.003N2) - 0.16N - 5
which reduces to
p = 58 + 0.567N - 0.0027N2
which is at a maximum when the level of N is such that using one (marginal) unit more or less would cause profit to decline, i.e., where the marginal rate of change of p with respect to N, i.e., dp /dN, is zero. This condition implies
dp /dN = 0.56 - 0.0054N = 0.
FIGURE 8.3 - Graph of Optimality Condition MVP = MC
Solving this equation for N, the profit-maximizing level of N is found to be 103 units per ha, the same as obtained previously using the equivalent criteria MVP = MC or MPP = pn/pg. With this optimal level of N, as before, the corresponding levels of G and p are, respectively, 121 units per ha and Rs 87 per ha.
Distinction needs to be recognized between maximum output and that level of output which maximizes profit (i.e., the economically optimal output). Again using the above nitrogen-grain example, maximum output is defined as that resulting from an input of N which if altered marginally in either direction would result in output decreasing or, stated another way, where the response curve peaks and has a slope of zero implying that the first derivative of grain output with respect to nitrogen input (i.e., dG/dN or MPP) is zero. Thus for the nitrogen-grain response equation G = 70 + 0.8N - 0.003N2, the output-maximizing level of N is found directly from dG/dN = 0.8 - 0.006N = 0 as 133 units per ha which compares with the profit-maximizing level of 103 units. The maximum level of output is thus G = 70 + 0.8(133) - 0.003(1332) = 123 units per ha with an associated profit of Rs 86 per ha which compare with the respective profit-maximizing levels of 121 units and Rs 87 per ha.
In a large-scale commercial situation with the input to be applied over a large area, the difference between these two levels could be seen as significant so that exactly 103 units of N would be applied per ha. But on small farms, especially those of a near-subsistence nature, the farmer would be likely just to throw on a few extra units of fertilizer in the knowledge that the amount which will give the 'best' crop is about the same as that which will give the 'best' net return.
Obviously, the achievement of optimal resource use is possible only if the resource is available in sufficient quantity or - what amounts to the same thing - only if the farmer has sufficient budget available to buy it in sufficient quantity.
Again using the nitrogen-grain example, it is easy to see if such a budget constraint would be present. The optimal input of N is 103 units per ha which would cost Rs 16.48. Suppose there is only a budget amount of B per ha available for purchase of N. The implied budget constraint is thus B³ 0.16N. It will be immediately apparent whether the necessary input cost of Rs 16.48 per hectare is greater or less than whatever budget level B might be operative; and if greater, the actual amount of N which can in fact be afforded. Thus a budget B of Rs 10 per ha would permit the budget-constrained use of only B/pn = 10/0.16 = 63 units of N per ha regardless of what the optimal level might be. This simple type of single-input situation hardly warrants a formal statement of the budget constraint in equation form. However, in multi-input and multi-process situations, formal statements of any constraints to optimization are required - see Dillon and Anderson (1990, pp. 40-53).
When the use of variable input factors is limited by a budget constraint, the law of diminishing returns implies that the limited budget should be spread across all the variable factors and all the technical production units (i.e., units of land area cropped or animals fed). The limited budget should not be concentrated on a limited number of variable factors or technical units. Figure 8.3 with its graph of declining MVP = 0.90(0.8 - 0.006N) for the response process TPP = 70 + 0.8N - 0.003N2 provides an illustration. (Note that this declining MVP is a reflection of diminishing returns to N in the response equation.) Faced with this response situation, suppose the farmer could only afford 80 units of N for his or her two hectares of crop. It would be best for 40 units of N to be allocated to each hectare rather than all 80 units to one hectare. The former strategy would generate a total profit (assuming the same prices as before) of Rs 152. In contrast, the latter strategy would only generate Rs 58 on the unfertilized hectare and Rs 85 on the fertilized hectare, giving a total profit of only Rs 143.
8.3.1 Optimization based on MVP = MC
8.3.2 Optimization by using the profit function
Optimization of two- and three-variable input processes can also be achieved by partial budgeting (using total relationships as in Section 8.2.1 above) but this method would be limited by the work involved in preparing the large number of necessary partial-budget tables. In practice, optimization of resource use in multi-variable input processes is best approached by an extension of the response equation method discussed in Section 8.2.3 above.
As outlined in Section 5.1, single-variable input production relationships of the type G = f(N) are usually a greatly oversimplified view of reality. More realistic would be the statement G = f(N, W/P, K, L, CK) in which grain yield is recognized as depending explicitly on the level of nitrogen and water while also acknowledging that soil phosphorus and potash status, amount of labour applied, cultivating frequency etc. are also important factors. More realistic still would be analysis which explicitly evaluates all of these factors as variable inputs. But usually a balance must be struck between achieving greater realism on the one hand and analytical capacity on the other. This is generally based on selection for analysis of only those input factors which (a) have significant economic relevance and (b) can be manipulated or controlled by management. (Many factors are not easily amenable to farmer manipulation: e.g., the necessity sometimes of simply accepting whatever volume of water comes down the irrigation supply channel. Other factors such as, e.g., rainfall and solar radiation, are totally beyond the farmer's control; from his or her perspective they are not decision factors except in so far as supplementary strategies - such as irrigation to overcome rainfall deficits - may be used to ameliorate his or her lack of control.)
Thus, in practice, analysis of most multi-variable input processes of Order Level 2 is limited to examining the simultaneous effects of two or three variable-input factors which are under the farmer's control. In contrast, analysis of the resources used in production function analysis of whole-farm systems of Order Level 10 might consider four, five or six categories of inputs as outlined, e.g., by Dillon and Hardaker (1993, pp. 221-224) and Heady and Dillon (1961, pp. 218-228). (The analysis of whole-farm systems using production functions is largely confined to work in Field D relating to policy guidance (Section 2.1.7) which is outside the scope of this discussion.)
Resource use in multi-variable input processes is optimized using an extension of the response equation method outlined in Section 8.2.3 above, regardless of whether two- or three- or n-variable inputs are involved. Here, for purposes of illustration, two variable inputs are assumed but the method extends directly to three or more variable input factors. Again the relevant relationships are the physical response function, the MVP of each variable input used and the unit price of each input in relation to the unit price of the output. The only operational change is that the partial derivative of each variable input is now used and the MVP of each variable input is now obtained as this partial derivative times the unit price of the input.
The optimizing rule is to use each input at the level at which the ratio of its marginal physical product to its unit price is equal to the inverse of the unit product price. Thus the response process Y = f(X1, X2) is optimized when
MPP1/p1 = 1/py = MPP2/p2
where MPPi denotes the MPP of Xi. To illustrate the procedure it is assumed that a response function relating grain output (denoted by G) to input of nitrogen (N) and water (W) could be obtained by fitting some appropriate equation to input-output data from a field trial to obtain the response function G = f(N, W). The unit price of grain is given as p and the unit costs of the two inputs are given as pn and pw respectively.
Given the response relationship G = f(N, W), the marginal value product of N, denoted by MVPn, is defined as pg(MPPn) = pg(¶ G/¶ N) where ¶ G/¶ N denotes the partial derivative of G with respect to N. Likewise, MVPw = pg(¶ G/¶ W).
Setting these respective marginal value products equal to their respective input prices (i.e., the marginal cost of each input factor), profit maximization implies that:
(i) pg(¶ G/¶ N) = pn
(ii) pg(¶ G/¶ W) = pw
Dividing each of these equations by pg gives
(iii) ¶ G/¶ N = pn/pg
(iv) ¶ G/¶ W = pw/pg
Dividing (iii) and (iv) through, respectively, by the prices pn and pw,
(v) (¶ G/¶ N)/pn = 1/pg
(vi) (¶ G/¶ W)/pw = 1/pg
Since both equations (v) and (vi) are equal to 1/pg they are equal to each other and, noting that the left-hand numerators are the respective marginal physical products of N and W, equations (v) and (vi) can be rewritten as the optimality condition:
(vii) MPPn/pn = MPPw/pw = 1/pg
or, equivalently, after multiplying through by pg,
(viii) MPPn/pn = MPPw/pw = 1
Example
Given the response function
G = 500 + 100N + 4W - 5N2 - 2W2 + 2NW
for grain (G) in relation to nitrogen (N) and water (W) applications on a per ha technical unit basis and output and input unit prices of pg = Rs 20, pn = Rs 2 and pw = Rs 3, and working in terms of the basic optimization relationships MVPn = MCn and MVPw = MCw, (i.e., MVPn = 2 and MVPw = 3), corresponding to equations (i) and (ii) above:
2000 - 200N + 40W - 2 = 0
80 + 40N - 80W - 3 = 0.
Solving these two equations simultaneously for N and W (e.g., by multiplying the first by two and adding the result to the second to eliminate the W term), the optimal input levels are obtained as 11.31 units of N and 6.62 units of W per technical unit with a corresponding optimal yield of G = 1 080 units per ha. Substituting these derived values of N and W into equation (viii) shows that they satisfy the optimality condition.
As noted previously, often a more convenient way of approaching optimization is to work directly with the profit equation. From this viewpoint the multi-input optimization problem is that of using each variable input factor up to a level at which the resultant difference between TVP and TC, i.e., p , is at a maximum. This will be achieved when the use of one more or one less (marginal) unit of the input factor would lead to a reduction in profit. This occurs at input levels at which the rate of change in profit, relative to each input, is zero - or, in mathematical terms, when the partial derivative of profit relative to each variable input factor appearing in the profit function p = TVP - VC - FC is zero.
As before, given the underlying physical response relationship, the first step is to convert this to value or TVP terms. Using the same response equation and prices as in Section 8.3.1:
TVP = 20(500 + 100N + 4W - 5N2 - 2W2 + 2NW).
On the cost side of the profit equation, variable costs are simply the amount of N used in the process times its unit price plus the amount of water used times its unit price, i.e., Npn + Wpw. Fixed costs are assumed to be Rs 10 per ha. Thus
p = TVP - VC - FC = (10 000 + 2 000N + 80W - 100N2 - 40W2 + 40NW) - (2N + 3W) - 10 = 9 990 + 1 998N + 77W - 100N2 - 40W2 + 40NW.
Taking partial derivatives of pi with respect to N and W, and setting these equal to zero (because such equality defines the condition for profit maximization), the following two equations are obtained:
¶ p /¶ N = 1 998 - 200N + 40W = 0
¶ p /¶ W = 77 + 40N - 80W = 0.
Solving these two equations simultaneously for the values of N and W at which profit is at a maximum, these values are 11.31 units of N and 6.62 units of W per technical unit, the same as were obtained in Section 8.3.1 using the less direct MVP = MC approach.
Note that fixed costs (FC) are irrelevant to determination of marginal rates of profit change with respect to variable inputs. This is because, by their nature, FC are invariant relative to input levels and profit. Thus, unlike VC, they play no part in the profit optimizing decision.
8.4.1 Using existing data
8.4.2 Data from on-farm experiments
8.4.3 Trials with 'permanent' or long-term crops
Possible sources of data for response analysis are briefly reviewed.
In most Asian-Pacific countries there exists a large volume of potentially useful data relating to the major crops and their inputs/outputs in specific farming environments. In colonial times the emphasis was on the export crops (tea, rubber, coconut, oilpalm, cacao, jute etc); the village or 'minor' (often staple!) crops were relatively neglected. In post-colonial decades, emphasis has shifted to the major food crops (paddy and the other cereals, food legumes and root crops).
Commodity-specific national research institutes such as the Rubber Research Institute of Malaysia, the Coconut Research Institutes of the Philippines and Sri Lanka, the Tea Research Institute of Sri Lanka etc. continue to generate much information from field experiments and this work is now generally broadened to include other crops grown in association with the main export crops (e.g., food crops inter-planted in young rubber and similar under-cropping with coconut). As well, much response information on staple crops and on livestock is available from such international agricultural research institutes as AVRDC (vegetables), CGPRT Centre (coarse grains, pulses, roots, tubers), CIAT (beans, cassava, tropical forages), CIMMYT (maize, wheat), CIP (potato, sweet potato), ICLARM (aquaculture), ICRAF (agroforestry), ICRISAT (sorghum, finger millet, pearl millet, chickpea, pigeonpea, groundnut), ILRI (cattle, buffalo, sheep, goats) and IRRI (rice).
Too, in spite of their general past neglect in comparison with the export crops, some of the village crops were in fact intensively investigated decades ago: the libraries of Bogor, Kuala Lumpur, Los Baños, Calcutta, Kandy, Islamabad ... as well as the archives of the ex-colonial administrations are depositories of vast amounts of information covering a wide range of input/output relationships for field and tree crops and livestock. This is now often neglected but a considerable part of it is still relevant. Of particular value (and fascination) are the old monographs and Agriculture Department journals of the 1920s and 1930s. This was indeed a golden age in terms of the range of crops investigated and practical guidelines which were developed for their management: kitul palm, palmyrah, areca, ginger, breadfruit, citronella, sago, cassava, nipah palm ... are only some of the 'people's crops' that were studied - and only now are some of these crops being officially rediscovered.
Useful data from this earlier period usually concern yield relationships relative to such husbandry variables as plant spacing, pruning method, manure application, crop age at harvest (Figure 8.4), harvest frequency and water application. These relationships are seldom presented as formal response functions but as tables of input/output data from which such functions may be constructed. As an example, Figure 8.4 shows the relationship between crop age and yield for two varieties of cassava as determined from field trials conducted in the 1920s. Assuming that the varieties are still current and the environments are similar, the response curves shown might well be of direct present use. Or, if the varieties have been superseded, the relationships shown might at least serve as a guide in structuring an on-farm trial to up-date such information.2
2 Continuing validity of data from past crop trials will obviously depend on whether or not the old varieties are still current. In general, the major short-term food-crop varieties are frequently superseded by new cultivars, as are some of the major (export) tree crops such as rubber and oilpalm. But most tree crops and most minor crops are replaced by improved varieties only once in several decades, if at all.
When working with farmers in Modes 3 and 4, i.e., respectively, diagnosis of system weaknesses and prescription of solutions, most farm analysts (consultants, extension officers, village development agents) will be able to organize simple field trials in cooperation with farmers for such short-term crops as paddy, maize, sorghum, wheat, clover etc. These will typically involve maintaining the trial over some short period of three to six months. They will also be able to execute on-farm trials involving those aspects of livestock production which involve a rapid short-term response, e.g., feeding at different input levels in relation to yield of milk or fish, but not, e.g., long-term breeding trials aimed at the genetic improvement of livestock.
FIGURE 8.4 Sketch of Field-trial Results for Two Varieties of Cassava

As a consequence of the recognition of the usefulness of a systems approach to farm research and of the benefits of farmer participation in such research, much has been written on the need for and conduct of on-farm trials - see, e.g., Amir and Knipscheer (1989), Dillon and Anderson (1990. Ch. 8), Farming Systems Support Project (1987a, b, c), Hildebrand and Poey (1985), Mutsaers and Walker (1991), Mutsaers, Weber, Walker and Fischer (1997), Nagy and Sanders (1990), Norman, Worman, Siebert and Modiakgotia (1995) and Tripp and Woolley (1989). The following points are offered as a general guide.
Selecting the farm: In setting up a farm experiment on behalf of a group of farmers or village the trial should be located on a farm which is as representative as possible of all those other farms to which the results may be relevant.
Selecting the farmer: Selection of the cooperating farmer on whose land the experiment is to be located is usually more difficult. The farmer should be representative of his or her peer group, neither outstandingly advantaged or disadvantaged; but in addition he or she should be an opinion-leader though not an official. However, the most cooperative farm families are often those of the village chief or other officials (local-level officials are often also farmers); and these people often enjoy significant farming advantages in owning the best lands, getting priority in water supply, having access to credit etc. These factors, which may be favourable to the successful technical conduct of an on-farm trial might later become disadvantages when they are cited as reasons why 'ordinary' villagers don't or can't apply trial results.
Identifying the decision-maker: It should not be assumed that the male head of the household is the 'farmer' or 'decision-maker'. In many societies the farmers, as managers and operators if not as resource owners, are women. Obviously any on-farm trial must be carefully explained to and if possible planned with all relevant members of the cooperating household, not just its nominal head.
Ensuring maximum participation: It is essential that on-farm experiments involve the maximum number of potential beneficiaries at all stages of planning, execution and evaluation. While most farmers will not understand the concepts of resource optimization as these have been presented in this chapter, they will understand when 'optimality' is presented in down-to-earth terms and supported by visual demonstration.
Defining the subject for investigation: The analyst will probably approach the setting up of a trial with a fairly firm idea of what is to be investigated. But unless he or she sits down and discusses this with the household (or even better, the village), he or she might not learn, e.g., (a) that the object of the trial is judged by them to be not important; or (b) that, although important, there are even more important relationships which should be investigated first; or (c) that there are better ways of measuring the proposed relationships than those the analyst had intended to use; or (d) that even though the trial might perhaps yield positive results, the village would have absolutely no intention of applying them because of local economic/institutional/social/political factors of which the analyst, as an outsider, is ignorant.
Defining the trial boundaries: Regarding the trial as a system, its boundaries should be carefully defined to include secondary outputs or side effects even when these cannot be accurately measured. An example is offered by the practice of many Sri Lankan farmers of using much more water on paddy than is needed for optimal rice output. The extra water is used to reduce weed growth. Being natural economists, the farmers have figured out the optimal balance between grain lost due to excessive water and weeding-labour saved. A water input/grain output trial which excluded consideration of the labour-saving output of water would be of little practical relevance to these villagers.
If working with large farms/estates growing perennial tree crops, analysts and development officers will be able to conduct both short- and long-term trials. Short-term trials will involve factors having a rapid short-term response, e.g., yield in relation to fertilizer application, or yield in relation to harvest frequency. Long-term trials will aim at evaluation of the effect on yield of such factors as tree variety and spacing, or pruning patterns, or the mutual effects of different species in a tree-crop mix. Because of the long periods of time required to obtain results and difficulties of trial control, long-term trials with perennial crops will usually not be practicable on small farms; only short-term (usually seasonal) trials of some aspects of their production will be possible.
Figure 8.5 shows the results of a typical long-term tree-crop trial relating the yield of cashew nuts in response to a range of tree spacings (and their corresponding input levels of trees per acre). Obviously, because of the long waiting period involved before the trees begin to bear and the cost of monitoring this type of trial over many years, it would not be practicable to conduct it in a small-farm environment. The yield curves of Figure 8.5 refer to only the first few years of this experiment; the effect of 'crowding' at the higher tree-population levels (closer spacing levels), which will later become operative through competition for moisture and nutrients, is not yet apparent. It would be necessary to continue the trial over several more years in order to quantify the full effects of spacing on yield. Such a trial might have to be monitored over 20 years or so (over which time the response schedules would probably take on a more conventional curvature indicating diminishing returns as tree density increases with closer spacing). Note also that this example is useful in illustrating that there might well be more than one basis for measuring output in terms of the technical unit of production used. Here, yield per unit of land area would be appropriate for a farm where land is in short supply, while yield per tree would be appropriate if the farmer's cashew is scattered over a relatively large area (and perhaps intercropped).
Obtaining long-term data from cross-sectional surveys
One way that long-term tree-crop 'trials' can be 'conducted' rapidly is to use cross-sectional data from a survey of tree-crop stands on a sample of farms as a surrogate. This approach is illustrated in Figure 8.6 which relates yield of cacao to tree age and population density, and thus depicts the two-input process Y = f(age, density). The data were obtained by a survey of a sample of farms, all growing cacao of the same variety on similar soils and inter-planted with a similar mix of other tree crops of different ages and densities. Although the data from this type of cross-sectional survey come from many farms, it can usually be used as a guide for an individual subject farm as long as this is similar in essential respects to the surveyed farms. The main point is that data which would otherwise take 25, 30... years to obtain can often be obtained in two or three weeks by a field survey.
The data on which response analysis is based and the information which it gives can never be perfect (Dillon and Anderson, Chs 7 and 8). First, there will always be uncertainty about the effect of such uncontrolled factors as climate, pests and disease. Second, relative to its proposed use, the data on which the response relationship is based may be imperfect, e.g., it may relate to a different location (the problem of location specificity) or to a superseded variety or a soil of different fertility status. Third, the assumed response relationship can only be interpreted as an average relationship across some set of, preferably, representative observations. The better the spread of these observations across time and space, the more reliable will response analysis be. Data from trials of a multi-year multi-location nature are to be preferred to data from a trial conducted only once in a single location. Fourth, prices - particularly of output - may not be known with certainty. Fifth, every farm household, farmer and farm is unique. Resource qualities vary between farms. Farmers vary in their managerial ability, their knowledge, their opportunity costs, their assessment of uncertainty and their reactions to it, and in their preferences about the possibilities they see as open to them.
FIGURE 8.5 - Results of a Cashew Spacing Trial
Source; North-wood and Tsaliris (1967).
For all the above reasons, information based on response analysis should be used with caution and judgement. While it can provide useful guidelines (as illustrated relative to Figures 7.2 and 7.3), response analysis is no panacea to the problem of deciding on the best allocation of resources to production processes and activities. Generally, from the perspective of a farm management analyst working with farmers, a simple graphical approach to the appraisal of response processes is likely to be more fruitful than a more complex full-blown multi-variable analysis based on response equations. This is especially so relative to small farms involving a subsistence component.
FIGURE 8.6 - Sketch of Cacao Yield relative to Tree Density and Age from a Farm Survey in Sri Lanka
Source: Based on a 1974 survey by P.C. Kuhonta and others.
Amir, P. and H.C. Knipscheer (1989). Conducting On-farm Animal Research: Procedures and Economic Analysis, Winrock International Institute for Agricultural Development, Morrilton.
Beattie, B.R. and C.R. Taylor (1985). The Economics of Production, Wiley, New York.
Debertin, D.L. (1986). Agricultural Production Economics, Macmillan, New York.
Dillon, J.L. and J.R. Anderson (1990). The Analysis of Response in Crop and Livestock Production, 3rd edn, Pergamon Press, Oxford.
Dillon, J.L. and J.B. Hardaker (1993). Farm Management Research for Small Farmer Development, FAO Farm Systems Management Series No. 6, Food and Agriculture Organization of the United Nations, Rome.
Doll, J.P. and F. Orazem (1984). Production Economics: Theory with Applications, 2nd edn, Wiley, New York.
Farming Systems Support Project (1987a). Diagnosis in Farming Systems Research and Extension, FSR/E Training Units: Vol. I, International Programs, Institute of Food and Agricultural Sciences, University of Florida, Gainesville.
Farming Systems Support Project (1987b). Design Techniques for On-farm Experimentation, FSR/E Training Units: Vol. II, International Programs, Institute of Food and Agricultural Sciences, University of Florida, Gainesville.
Farming Systems Support Project (1987c). Analysis and Interpretation of On-farm Experimentation, FRS/E Training Units: Vol. III, International Programs, Institute of Food and Agricultural Sciences, University of Florida, Gainesville.
Heady, E.O. and S. Bhide (1984). Livestock Response Functions, Iowa State University Press, Ames.
Heady, E.O. and J.L. Dillon (1961). Agricultural Production Functions, Iowa State University Press, Ames.
Hexem, R.W. and E.O. Heady (1978). Water Production Functions for Irrigated Agriculture, Iowa State University Press, Ames.
Hildebrand, P.E. and F. Poey (1985). On-farm Agronomic Trials in Farming Systems Research and Extension, Lynne Rienner Publishers Inc., Boulder.
Mutsaers, H.J.W. and P. Walker (eds) (1991). On-farm Research in Theory and Practice. International Institute of Tropical Agriculture, Ibadan.
Mutsaers. H.J.W., G.K. Weber, P. Walker and N.M. Fischer (1997). A Field Guide for On-farm Experimentation, International Institute of Tropical Agriculture, Ibadan.
Nagy, J.G. and J.H. Sanders (1991). 'Agricultural Technology Development and Dissemination within a Farming Systems Perspective', Agricultural Systems 32: 305-320.
Norman, D.W., F.D. Worman, J.D. Siebert and E. Modiakgotia (1995). The Farming Systems Approach to Development and Appropriate Technology Generation, FAO Farm Systems Management Series No. 10, Food and Agriculture Organization of the United Nations, Rome.
Northwood, P.J. and A. Tsaliris (1967). 'Cashew Nut Production in Southern Tanzania: III - Early Yields from a Cashew Spacing Experiment', East African Agricultural and Forestry Journal 33: 81-82.
Rae, A.N. (1977). Crop Management Economics, Crosby Lockwood Staples, London.
Tripp, R. and J. Woolley (1989). The Planning Stage of On-farm Research: Identifying Factors for Experimentation, CIMMYT, Mexico, D.F. and CIAT, Cali.
van der Zijl, C.E. (1930). Improvement of Cassava Cultivation by Field Experiments, Agricultural University, Wageningen.