Considérons un ensemble de données concernant la densité du bois obtenues à partir d’observations d’un ensemble, choisi au hasard, de tiges appartenant à un ensemble d’espèces de bambous. Supposons que l’on ait t espèces et r observations pour chaque espèce. Les résultats peuvent être rassemblés en tableau, selon le modèle ci-après :

Note: Dans ce tableau, une période (.) en indice dénote la somme sur cet indice.

La théorie qui sous-tend l’analyse de variance est complexe et risquerait de rebuter le lecteur profane. C’est pourquoi nous avons choisi de présenter une dérivation heuristique des formules. Considérons les r observations concernant une espèce particulière quelconque, par exemple la i-ème. Leurs valeurs peuvent être différentes, ce qui démontre l’influence de nombreux facteurs externes sur les observations de tiges de cette espèce. Cette influence peut-être mesurée par les écarts des observations individuelles à la moyenne. Il est préférable d’élever les écarts au carré car les écarts simples pourraient s’éliminer lors de la sommation. L’amplitude d’une variation aléatoire affectant les observations concernant la i-ème espèce est donnée par l’expression

= (3.13)

Pour chaque espèce, la variation produite par les sources externes reflète l’influence des facteurs incontrôlés, qui peut être globalement estimée par sommation. La variation totale observée, imputable à des facteurs externes, également connue sous le nom de somme des carrés due aux erreurs (SSE) est donnée par

SSE = (3.14)

Outre les fluctuations aléatoires, différentes espèces peuvent avoir différents effets sur la réponse moyenne. La variation due à la i-ème espèce dans les r observations est donc

(3.15)

La variation due aux différences entre les espèces est donc donnée par la relation

SS due aux espèces = SSS = (3.16)

algébriquement équivalente à

SSS =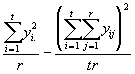 (3.17)

Le second terme de l’équation (3.17) est appelé facteur de correction (C.F.).

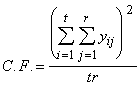(3.18)

Pour finir, nous devons trouver la variation totale présente dans toutes les observations. Cette dernière est donnée par la somme des carrés des écarts de toutes les réponses à leur moyenne générale. En symboles,

SSTO = 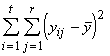(3.19)

=

=

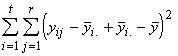
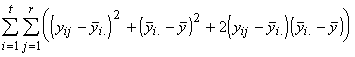
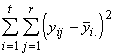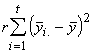= + (3.20)

où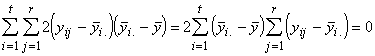

La variation totale des réponses peut donc s’exprimer comme la somme des variations entre les espèces et des variations au sein d’une espèce. C’est là l’essence même de l’analyse de la variance.

Aux fins des calculs, SSTO s’obtient aussi comme

SSTO =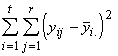+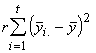= 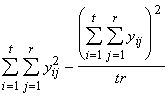(3.21)

Si la répartition de la variabilité totale entre ce qui est dû aux différences entre espèces et ce qui est dû aux facteurs externes a une valeur informative, elle n’est guère utile en elle même pour pousser plus avant l’interprétation. En effet, ces valeurs dépendent du nombre d’espèces et du nombre d’observations effectuées sur chaque espèce. Pour éliminer l’effet dû au nombre d’observations, on réduit les mesures de la variabilité observée à une variabilité par observation, c’est à dire à la moyenne de la somme des carrés. Etant donné qu’il y a au total rt observations, dont on tire la somme totale des carrés, il est évident que l’on peut calculer la moyenne de la somme des carrés en divisant la somme totale des carrés par rt. Au lieu de cela, on la divise par (rt-1), qui est le nombre total d’observations moins une. Ce diviseur est appelé degré de liberté et indique le nombre d’écarts à la moyenne indépendants qui contribuent au calcul de la variation totale. Par conséquent,

Moyenne de la somme des carrés due aux espèces = MSS = (3.22)

Moyenne de la somme des carrés due aux erreurs = MSE = (3.23)

Le calcul de la moyenne des carrés des espèces et de la moyenne des carrés des erreurs est crucial pour vérifier la signification des différences entre les moyennes des espèces. Ici, l’hypothèse nulle qui est testée est que toutes les moyennes de population des espèces sont égales, c’est à dire :

Dans cette hypothèse, les deux moyennes des carrés ci-dessus représenteront deux estimations indépendantes du même effet aléatoire, autrement dit MSS et MSE fournissent une estimation de la même variance. On peut maintenant tester l’hypothèse " les effets des espèces sont égaux " à l’aide du critère F, où F est le rapport de MSS à MSE. Le critère F suit une distribution F avec (t-1) et t(r-1) degrés de liberté. La signification de F peut être déterminée de la manière habituelle en se reportant à la table de F (Annexe 3). Si la valeur calculée de F est supérieure à la valeur indiquée par la table, l’hypothèse est rejetée. Cela signifie que les observations concernant au moins une paire d’espèces ont mis en évidence des différences significatives.

Les résultats qui précèdent peuvent être récapitulés dans un tableau d’analyse de variance, présenté comme suit

Table 3.4. Tableau d’analyse de variance

Nous illustrerons ce qui précède à l’aide des données du Tableau 3.5. Celles-ci représentent un ensemble d’observations sur la densité du bois, dérivées d’un ensemble, prélevé au hasard, de tiges de cinq espèces de bambous.

L’analyse de la variance des données de l’échantillon se fait en plusieurs étapes.

*Etape 1. Calculer les totaux des espèces, la moyenne des espèces, le total général et la moyenne générale (comme dans le Tableau 3.5) . Ici le nombre d’espèces = t = 5 et le nombre d’observations = r = 3.

Tableau 3.5. Densité du bois (g/cc) observée sur un ensemble, prélevé au hasard, de tiges appartenant à différentes espèces de bambous.

*Etape 2. Calcul er le facteur de correction C.F à l’aide de l’équation (3.18).

C.F.

*Etape 3. Calculer la somme totale des carrés à l’aide de l’équation (3.21).

SSTO = (0.58)² + (0.53)² + . . .+ (0.63)² -

= 0.0765

*Etape 4. Calculer la somme des carrés relative aux espèces à l’aide de l’équation (3.17).

SSS =

= 0.0307

*Etape 5. Calculer la somme des carrés des erreurs grâce à la relation SSE = SSTO - SSS

SSE = 0.0765 - 0.0307

= 0.0458

*Etape 6. Calculer la moyenne de la somme des carrés pour les espèces et les erreurs. Celles-ci sont données par les équations (3.22) et (3.23).

MSS =

= 0.0153

MSE =

= 0.0038

*Etape 7. Calculer le rapport F

F =

=

= 4.0108

*Etape 8. Résumer les résultats comme dans le Tableau 3.6.

Tableau 3.6. Tableau de l’analyse de la variance des données du Tableau 3.5.

Comparer la valeur calculée et la valeur tabulaire de F, pour 4 et 10 degrés de liberté. Dans notre exemple, la valeur calculée du rapport F (1.73) est inférieure à la valeur tabulaire (3.48), au seuil de signification de 5%. On en conclut qu’il n’y a pas de différences significatives entre les moyennes des différentes espèces.

3.7. Transformation de données

On a déjà dit dans la section précédente que la validité de l’analyse de variance dépend de certains hypothèses importantes. L’analyse peut aboutir à des conclusions fausses si toutes ces hypothèses ne sont pas respectées, ce qui est par exemple relativement courant pour l’hypothèse de la variance constante des erreurs. Dans ce cas, l’une des possibilités est d’effectuer une analyse de variance pondérée, en vertu de laquelle chaque observation est pondérée par l’inverse de sa variance. Ceci suppose d’estimer la variance de chaque observation, ce qui n’est pas toujours possible. Souvent, les données subissent certaines transformations d’échelle, de sorte qu’à l’échelle transformée, l’hypothèse de la variance constante est réalisée. Certaines de ces transformations peuvent aussi corriger des écarts des observations par rapport à la normale, du fait qu’une différence de variance est souvent aussi liée à la distribution de la variable. On dispose de méthodes spécifiques pour identifier la transformation requise pour tout ensemble de donnée particulier (Montgomery et Peck, 1982), mais on peut aussi avoir recours à certaines formes de transformation normalisées suivant la nature des données. Les plus courantes sont la transformation logarithmique, la transformation racine carrée et la transformation angulaire.

Lorsque les données se présentent sous forme de nombres entiers représentant des catégories de grande étendue, les variances des observations à l’intérieur de chaque groupe sont généralement proportionnelles aux carrés des moyennes du groupe. Pour ce type de données, la transformation logarithmique est conseillée. La comparaison d’une parcelle témoin de moyennes de groupe avec l’écart-type du groupe mettra en évidence une relation linéaire. Les données issues d’une expérience réalisée avec différents types d’insecticides fournissent un bon exemple. Pour l’insecticide efficace, les catégories d’insectes dans l’unité expérimentale traitée peuvent être peu étendues, alors que pour les insecticides inefficaces, les catégories peuvent comprendre de 100 à plusieurs milliers d’insectes. Dans le cas de données avec des zéros, il est conseillé d’ajouter 1 à chaque observation avant de procéder à la transformation. La transformation logarithmique est particulièrement efficace pour normaliser les distributions désaxées vers la droite. Elle est parfois aussi employée pour calculer l’additivité des effets.

La méthode consistant à convertir les observations originelles à l’ordre de grandeur de la racine carrée, en prenant la racine carrée de chaque observation, est connue sous le nom de transformation racine carrée. Elle est appropriée lorsque la variance est proportionnelle à la moyenne, ce que l’on peut voir sur un graphique de variances de groupe et de moyennes de groupes. Une relation linéaire entre la moyenne et la variance est couramment observée lorsque les données sont de petits nombres entiers (ex : catégories de sauvageons par quadrat, adventices par parcelle, vers de terre par mètre carré de sol, insectes pris au piège etc…) Lorsque les valeurs observées sont comprises dans une fourchette allant de 1 à 10, et surtout lorsqu’elles ont des zéros, la transformation devrait être , . La transformation du type est également employée pour certaines raisons théoriques.

Dans le cas de proportions dérivées de données de fréquence, la proportion observée p peut être mise sous une nouvelle forme . Cette méthode est connue sous le nom de transformation angulaire ou de transformation arc-sinus. Toutefois, lorsque presque toutes les valeurs des données sont comprises entre 0,3 et 0,7, cette transformation n’est pas nécessaire. En outre, elle n’est pas applicable aux proportions ou aux pourcentages qui n’ont pas été obtenus expérimentalement. Ainsi, les pourcentages de marques, de profit, de protéines dans les graines, la teneur en huile des semences etc…ne peuvent pas être soumis à une transformation angulaire. La transformation angulaire n’est pas valable lorsque dans les données p prend les valeurs 0 ou 1. On l’améliorera en remplaçant, avant de prendre des valeurs angulaires, 0 par (1/4n) et 1 par [1-(1/4n)], où n est le nombre d’observations sur la base desquelles est estimé p pour chaque groupe.

Pour illustrer la transformation angulaire par un exemple, prenons les données du Tableau 3.7 qui représentent le pourcentage de racines obtenu après avoir appliqué pendant six mois un traitement hormonal, à des doses différentes, à des boutures de tiges d’une espèce d’arbre. Trois lots, contenant chacun dix boutures, ont été trempés dans une solution hormonale, à des dosages différents. L’hormone a été essayée à trois concentrations et l’expérience comprenait un lot témoin non traité. Le pourcentage de racines de chaque lot de boutures a été obtenu en divisant le nombre de boutures à racines par le nombre de boutures compris dans un lot.

Tableau 3.7. Pourcentage de boutures obtenu au bout de six mois de traitement

Les données du Tableau 3.7 ont été transformées à l’échelle angulaire, à l’aide de la fonction, après avoir remplacé les valeurs de " 0 " par (1/4n) où n =10. Les valeurs de la fonction pour différentes valeurs de p peuvent aussi être extraites du Tableau (X) of Fisher et Yates (1963). Les données transformées du Tableau 3.7 sont rassemblées dans le Tableau 3.8.

Table 3.8. Données du Tableau 3.7 transformées à l’échelle angulaire.

Afin de voir si les effets des traitements présentent des différences significatives, une analyse de variance à un facteur peut être effectuée selon la méthode indiquée dans la section 3.6 sur les données transformées. Les résultats de l’analyse de variance sont présentés au Tableau 3.9.

Tableau 3.9. Analyse de la variance des données transformées du Tableau 3.8.

* significatif au seuil de 5%.

Avant de conclure cette section, il convient d’ajouter une note de caractère général. Une fois que la transformation a été faite, l’analyse est effectuée avec les données transformées et toutes les conclusions sont tirées à l’échelle transformée. Toutefois, lors de la présentation des résultats, les moyennes et leurs écarts types sont reconverties aux unités originelles. Lors de cette reconversion, certaines corrections doivent être apportées aux moyennes. Dans le cas de données soumises à une transformation logarithmique, si la valeur moyenne est y, la valeur moyenne des unités originelles sera au lieu de . Avec la transformation racine carrée, la moyenne à l’échelle initiale serait au lieu de où représente la variance de . On ne fait généralement pas ces corrections dans le cas d’une transformation angulaire. Pour la transformation angulaire, la transformation inverse serait p = (sin q )².

3.8. Corrélation

Dans beaucoup de systèmes naturels, les changements d’un attribut s’accompagnent de variations d’un autre attribut, et il existe une relation définie entre les deux. En d’autres termes, il existe une corrélation entre les deux variables. Par exemple, plusieurs propriétés des sols, comme la teneur en azote, la teneur en carbone organique ou le pH, sont corrélées et varient de façon concomitante. On a observé une forte corrélation entre plusieurs caractéristiques morphométriques d’un arbre. Dans de telles situations, il peut être intéressant pour un chercheur de mesurer l’importance de cette relation. Si (x_i,y_i); i = 1, ..., n, est un ensemble d’observations appariées effectuées sur n unités d’échantillonnage indépendantes, une mesure de la relation linéaire entre deux variables est donnée par la quantité suivante, appelée coefficient de corrélation linéaire de Pearson, ou simplement coefficient de corrélation.

(3.24)

où Cov (x,y) = =

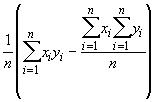
V(x) = =

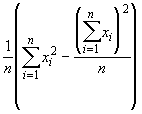
V(y) = =

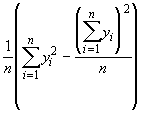
Ce paramètre statistique indique à la fois la direction et le degré de la relation existant entre deux caractères quantitatifs x et y. La valeur de r peut varier de –1 à +1, sans atteindre ces valeurs. Si la valeur de r est nulle, cela signifie qu’il n’y a pas de relation linéaire entre les deux variables concernées (il peut toutefois y avoir une relation non-linéaire). La relation linéaire est forte lorsque la valeur de r approche –1 ou +1. Une valeur négative de r indique que si la valeur d’une variable augmente, celle de l’autre diminue. Au contraire, une valeur positive indique une relation directe, c’est à dire que l’augmentation de la valeur d’une variable est associée à une augmentation de la valeur de l’autre. Un changement d’origine, d’échelle, ou d’origine et d’échelle est sans incidence sur le coefficient de corrélation. Lorsque l’on ajoute ou soustrait un terme constant aux valeurs d’une variable, on dit que l’on a changé d’origine, alors que lorsque l’on multiplie ou divise par un terme constant les valeurs d’une variable, on parle de changement d’échelle.

A titre d’exemple, considérons les données du Tableau 3.10 concernant le pH et la teneur en carbone organique mesurés dans des échantillons de terrain provenant de 15 fosses d’observation creusées dans des forêts naturelles.

Tableau 3.10. Valeurs du pH et de la teneur en carbone organique observées dans des échantillons de terrain prélevés dans des forêts naturelles.

Le coefficient de corrélation se calcule en plusieurs étapes.

*Etape 1. Calcul de la covariance de x et y et des variances de x et de y à l’aide de l’équation (3.24).

Cov (x,y) =

= 0.05

V(x) =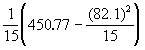

= 0.0940

V(y) =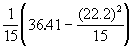

= 0.2367

*Etape 2. Calcul du coefficient de corrélation avec l’équation (3.24).

r =

= 0.3541

La signification d’une valeur du coefficient de corrélation calculée à partir d’un échantillon doit être testée pour confirmer l’existence d’une relation entre les deux variables, dans la population considérée. En général, on définit l’hypothèse nulle comme alors que l’hypothèse alternative est .

Pour n relativement petit, l’hypothèse nulle () peut être testée à l’aide du critère statistique

(3.25)

Ce critère statistique suit une distribution de Student t avec n-2 degrés de liberté.

Examinons les données du Tableau 3.10, où n = 15 et r = 0.3541. Pour tester si ou si, au contraire, , on calcule le critère statistique à l’aide de l’Equation (3.25).

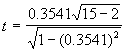= 1.3652

Dans la table de l’Annexe 2, la valeur critique de t est 2,160, pour 13 degrés de liberté, au seuil de signification a = 0,05. Comme la valeur calculée de t est inférieure à la valeur critique, on conclut que le pH et la teneur en carbone organique mesurés à partir d’échantillons de terrain ne sont pas corrélés de manière significative. Pour simplifier, on pourrait aussi se reporter à l’Annexe 5 qui donne les valeurs au-delà desquelles un coefficient de corrélation observé peut être déclaré significatif, pour un nombre donné d’observations au seuil de signification voulu.

Pour tester l’hypothèse , où r ₀ est une valeur donnée quelconque de r , on utilise la transformation Z de Fisher donnée par

(3.26)

où ln indique le logarithme naturel.

Pour tester l’hypothèse nulle, on choisit le critère statistique

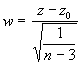(3.27)

où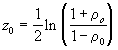

Le critère statistique w suit une loi de distribution normale standard.

Pour illustrer ceci par un exemple, prenons les données du Tableau 3.10, pour n = 15 et r = 0.3541. Supposons que l’on veuille tester l’hypothèse nulle = 0.6 ; on commencera par soumettre les valeurs de r et r à la transformation z.

= 0.3701

= 0.6932

La valeur du critère statistique sera donc

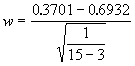= 1.16495

Etant donné que la valeur de w est inférieure à la valeur critique 1.96, le critère n’est pas significatif au seuil de signification de 5%. On en conclut que le coefficient de corrélation entre le pH et la teneur en carbone organique ne diffère pas de manière significative de 0.6.

3.9. Régression

Le coefficient de corrélation mesure le degré de la relation entre deux variables qui varient de façon concomitante, avec des effets qui se renforcent mutuellement. Dans certains cas, les changements relatifs à une variable sont provoqués par les variations d’une variable connexe, sans qu’il y ait de dépendance mutuelle. En d’autres termes, une variable est considérée comme dépendante des variations de l’autre variable, dans la mesure où elles dépendent de facteurs externes. Une telle relation entre deux variables est appelée régression. Lorsque ces relations sont exprimées sous forme mathématique, il est possible d’estimer la valeur d’une variable d’après la valeur de l’autre. Par exemple, le rendement de conversion photosynthétique et le coefficient de transpiration des arbres dépendent de conditions atmosphériques comme la température ou l’humidité, sans pour autant que l’on s’attende généralement à une relation inverse. Toutefois certaines variables sont souvent déclarées indépendantes uniquement au sens statistique, même dans des situations où des effets inverses sont concevables. Par exemple, dans une équation servant à estimer le volume, le volume des arbres est souvent considéré comme dépendant du diam&egr ave;tre à hauteur d’homme, même si le diamètre ne saurait être considéré comme indépendant des effets du volume des arbres au sens physique. C’est pourquoi, dans le contexte de la régression, les variables indépendantes sont souvent appelées variables exogènes (explicative), et la variable dépendante variable endogène (expliquée).

La variable dépendante est habituellement notée y et la variable indépendante x. Dans le cas où il n’y a que deux variables en jeu, la relation fonctionnelle est appelée régression simple. Si la relation entre les deux variables est linéaire, on parle de régression linéaire simple ; dans le cas contraire, la régression est dite non-linéaire. Lorsqu’une variable dépend d’au moins 2 variables indépendantes, la relation fonctionnelle entre la variable dépendante et l’ensemble des variables indépendantes est une régression multiple. Dans un souci de simplification, on se limitera ici à examiner le cas d’une régression linéaire simple. Pour des cas plus complexes, on se référera à Montgomery et Peck (1982).

La régression linéaire simple de y en x dans la population peut s’exprimer comme

(3.28)

où et sont des paramètres, appelés aussi coefficients de régression, et e est une déviation aléatoire pouvant dériver de la relation attendue. Si la valeur moyenne de e est zéro, l’équation (3.28) représente une droite de pente b et d’ordonnée à l’origine a . Autrement dit, a est la valeur présumée de y lorsque x prend la valeur zéro et b représente la variation attendue de y correspondant à une variation unitaire de la variable x. La pente d’une droite de régression linéaire peut être positive, négative ou nulle, selon la relation entre y et x.

En pratique, les valeurs de a et b doivent être estimées à partir d’observations des variables y et x effectuées sur un échantillon. Par exemple, pour estimer les paramètres d’une équation de régression proposée liant la température atmosphérique et le taux de transpiration des arbres, un certain nombre d’observations appariées sur la température et le taux de transpiration sont effectuées sur plusieurs arbres, à différents moments de la journée. Notons (x_i, y_i); i = 1, 2, . . ., n ces couples de valeurs, n étant le nombre de d’observations appariées indépendantes. Les valeurs de a et b sont estimées par la méthode des moindres carrés (Montgomery et Peck, 1982) de sorte que la somme des carrés des différences entre les valeurs observées et prévues soit minimale. Le processus d’estimation repose sur les hypothèses suivantes: i) Les valeurs de x sont non aléatoires ou fixes ; ii) Pour tout x, la variance de y est la même ; iii) Les valeurs de y observées pour différentes valeurs de x sont complètement indépendantes. Si l’une de ces hypothèses n’est pas vérifiée, il faut apporter les changements voulus. Pour les tests d’hypothèses se référant à des paramètres, une hypothèse additionnelle de normalité des erreurs est nécessaire.

En effet, les valeurs de a et b s’obtiennent grâce à la formule,

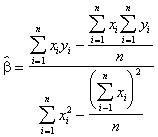(3.29)

(3.30)

L’équation représente la droite de régression ajustée, qui peut être utilisée pour estimer la valeur moyenne de la variable dépendante, y, associée à une valeur particulière de la variable indépendante, x. En général, il est plus sûr de limiter ces estimations à la fourchette des valeurs de x dans les données.

On peut obtenir une estimation des erreurs-type de avec la formule suivante :

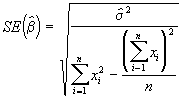(3.31)

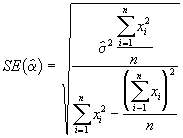(3.32)

où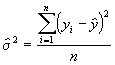

L’erreur-type d’une estimation, qui est l’écart-type de sa distribution d’échantillonnage, donne une indication du degré de fiabilité de cette estimation.

Nous illustrerons ce qui précède à l’aide des données du Tableau 3.11 qui présente les valeurs appariées du rendement photosynthétique et des radiations, obtenues à partir d’observations des feuilles d’une essence forestière spécifique. Dans cet exemple, la variable dépendante est le rendement photosynthétique et la variable indépendante est la quantité de lumière. La méthode de calcul de l’ajustement d’une régression linéaire est indiquée ci-dessous.

*Etape 1. Calculer les valeurs du numérateur et du dénominateur de l’équation (3.29) en utilisant les sommes, sommes des carrés et sommes des produits de x et y, dérivées du Tableau 3.11

= = 2.6906

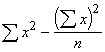= 12.70 - = 0.1508

Tableau 3.11. Données sur le rendement photosynthétique en mol m^-2s^-1 (y) et mesure de la radiation en mol m^-2s^-1 (x), observées sur une essence forestière

*Etape 2. Calculer les estimations de a et b avec les équations (3.29) et (3.30).

= 17.8422

12.60 - (17.8421)(0.9148)

= -3.7202

La droite de régression ajustée peut être utilisée pour estimer la valeur du rendement photosynthétique à un niveau de radiation quelconque donné, dans la limite des données. Ainsi, le rendement photosynthétique prévu, pour 1 mol m^-2s^-1 de lumière sera,

= 14.122

*Etape 3. Estimer s ² selon la formule définie dans l’Equation (3.32).

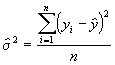= 0.6966

*Etape 4. Estimer les erreurs-type de à l’aide des Equations (3.31) et (3.32).

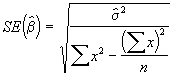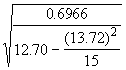= = 2.1495

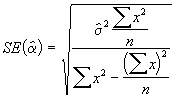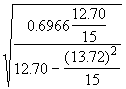= = 1.9778

Une fois que les paramètres de la fonction de régression ont été estimés, l’étape suivante est le test de signification statistique de la fonction de régression. Selon l’usage, on définit l’hypothèse nulle comme H₀: b = 0 en opposition à l’hypothèse alternative, H₁: b ¹ 0 ou (H₁: b < 0 ou H₁: b > 0, selon la nature présumée de la relation). Pour effectuer le test, on peut suivre la procédure de l’analyse de variance. Le concept de l’analyse de la variance a déjà été expliqué dans la Section 3.6, mais ses applications dans le cadre de la régression sont indiquées ci dessous, à l’aide des données du Tableau 3.11.

*Etape 1. Dresser un schéma de la table d’analyse de la variance.

Tableau 3.12. Représentation schématique d’une analyse de variance pour une analyse de régression.

*Etape 2. Calculer les différentes sommes des carrés, selon la méthode suivante :

Somme totale des carrés = 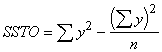(3.33)

= (7.58)² + (9.46)² + . . . + (14.36)² -

= 58.3514

Somme des carrés dus à la régression = SSR = 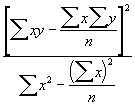(3.34)

=

= 48.0062

Somme des carrés dus à l’écart par rapport à la régression = SSE = SSTO - SSR (3.35)

=58.3514 - 48.0062 = 10.3452

*Etape 3. Entrer, comme indiqué dans le Tableau 3.13, les valeurs des sommes des carrés dans la table d’analyse de variance et effectuer les calculs restants.

Tableau 3.13. Analyse de variance pour l’équation de régression relative aux données du Tableau 3.11.

*Etape 4. Comparer la valeur calculée de F avec la valeur tabulaire correspondant à (1,n-2) degrés de liberté. Dans notre exemple, la valeur calculée (60.3244) est supérieure à la valeur tabulaire de F (4.67) correspondant à (1,13) degrés de liberté, au seuil de signification de 5%. La valeur de F est donc significative. Si la valeur calculée de F est significative, le coefficient de régression b diffère de 0 de manière significative. Exprimée en proportion de la somme totale des carrés, la somme des carrés due à la régression est appelée coefficient de détermination et mesure la quantité de variation de y imputable à la variation de x. En d’autres termes, le coefficient de détermination mesure la fraction de la variation de la variable dépendante expliquée par le modèle. Dans notre exemple, le coefficient de détermination (R²) est

(3.36)

= 0.8255