3.10. Analyse de covariance

Dans l’analyse de la variance, on évalue, en général, la signification d’un élément de variation connu, par rapport à la variation résiduelle inexpliquée. Un contrôle approprié est donc nécessaire pour réduire l’amplitude de la variation non contrôlée. A cette fin, on peut soit élargir le modèle à d’autres sources de variations mieux connues, soit exercer un contrôle délibéré sur de nombreuses variables ayant une incidence sur la réponse. A défaut d’un tel contrôle, des différences de groupe réelles ne seraient pas détectées en présence d’une variation résiduelle importante. Dans de nombreux cas, la variation existant au départ entre les unités d’observation est en grande partie responsable des variations de leurs réponses futures, et il devient nécessaire d’éliminer l’influence des variations endogènes entre les sujets de la comparaison des groupes étudiés. L’analyse de la covariance est l’une des méthodes employées pour réduire l’amplitude des erreurs inexpliquées. Dans un contexte expérimental, par exemple, on peut effectuer une analyse de la covariance lorsque l’on dispose d’observations sur une ou plusieurs variables corrélées provenant de chaque unité expérimentale, ainsi que d’ observations sur la variable de réponse considérée. Ces variables additionnelles reliées sont appelées covariables ou variables accessoires ou concomitantes. Il est indispensable qu’elles soient associées à la variable à l’étude. Par exemple, dans les essais de rendement, la variation du volume sur pied initial due à des facteurs externes, les effets résiduels des plantes antérieurement cultivées sur le site etc…, peuvent faire office de covariables.

L’analyse de covariance est une synthèse des méthodes de l’analyse de la variance et de la régression. Ce concept est étudié plus en détail ici dans le contexte d’une expérience portant sur l’étude d’une variable unique notée y et d’une covariable unique notée x. Notons t le nombre de groupes expérimentaux à comparer, chaque groupe étant constitué de r unités expérimentales. Dans cette situation, un modèle sous-jacent possible est

(3.37)

où y_ij est la réponse observée sur la j-ème unité expérimentale appartenant au i-ème groupe,

(i = 1, 2, …, t; j = 1, 2, …, r)

m _y est la moyenne globale de la population de y,

a _i est l’effet de l’appartenance au i-ème groupe,

b est le coefficient de régression de y en x à l’intérieur du groupe

x_ij est l’observation d’une variable accessoire sur la j-ième unité du ième groupe.

m _x est la moyenne globale de la covariable

e_ij sont les composantes des erreurs qui sont supposées être distribuées normalement et de manière indépendante avec une moyenne nulle et une variance constante de valeur .

L’analyse de la covariance étant essentiellement une extension de l’analyse de la variance, toutes les hypothèses sur lesquelles se fonde cette dernière s’appliquent aussi. Dans une analyse de la covariance, d’autres hypothèses sont également nécessaires, notamment i) la relation liant le caractère principal considéré y et la covariable x est linéaire ii) l’importance de la relation entre x et y est la même dans chaque groupe expérimental iii) la variation de la covariable n’est pas la résultante de différences internes au groupe.

Les différentes étapes de l’analyse de la covariance sont décrites ci-après.

*Etape 1. Dans l’analyse de la covariance, la première étape consiste à calculer la somme des carrés due aux différentes composantes, pour la variable y et la covariable x, comme pour une analyse de la variance, à l’aide des formules indiquées ci-après :

SS totale de y = SSTO(y) = 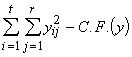(3.38)

où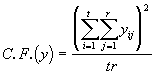 (3.39)

SS de y dans le Groupe= SSG(y) = 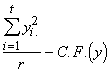(3.40)

SS de y dus aux Erreurs = SSE(y) = SSTO(y) -SSG(y) (3.41)

SS Totale de x = SSTO(x) = 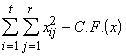(3.42)

où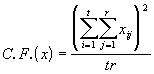 (3.43)

SS de x dans le Groupe = SSG(x) = 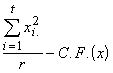(3.44)

SS de x dus aux Erreurs = SSE(x) = SSTO(x) - SSG(x) (3.45)

*Etape 2. Calculer comme suit la somme des produits de x et y.

SP Totale= SPTO(xy) = 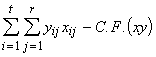(3.46)

où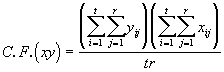 (3.47)

SP dans le Groupe = SPG(xy) = 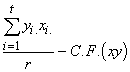(3.48)

SP dus aux erreurs = SPE(xy) = SSTO(xy) - SSG(xy) (3.49)

*Etape 3. L’étape suivante consiste à vérifier si la covariable est affectée par les groupes expérimentaux. Si les groupes n’ont aucune influence sur x, il ne doit pas y avoir de différences significatives entre les groupes par rapport à x. Le coefficient de régression à l’intérieur des groupes est donné par la relation

(3.50)

On peut tester la signification de à l’aide du test F. Le critère de test statistique F est donné par

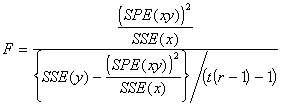(3.51)

Le critère statistique F suit une loi de F avec 1 et t(r-1)-1 degrés de liberté. Si le coefficient de régression est significatif, on procède à des ajustements de la somme des carrés de y pour des variations de x. Dans le cas contraire, les ajustements sont inutiles.

*Etape 4. Des valeurs ajustées de y sont calculées comme suit:

SS totale Ajustée de y = Adj. SSTO(y) = SSTO(y) - 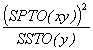(3.52)

SS Ajustée des erreurs de y = Adj. SSE(y) = SSE(y) - (3.53)

SS Ajustée de y dans le groupe = Adj. SSG(y)= Adj. SSTO(y) - Adj. SSE(y) (3.54)

Par convention, on regroupe tous ces résultats dans un seul tableau (voir Tableau 3.14).

*Etape 5. Les valeurs ajustées des moyennes de chaque groupe s’obtiennent avec la formule

(3.55)

L’erreur-type dans l’appréciation de la différence entre deux moyennes ajustées est donnée par:

SE(d) = 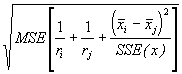(3.56)

où les symboles ont les significations habituelles.

Si le nombre de répétitions est le même pour tous les groupes et si les moyennes des valeurs globales de on a,

SE(d) = 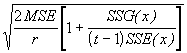(3.57)

Tableau 3.14. Table d’analyse de la covariance

Utilisons les données du Tableau 3.15 pour montrer comment s’effectue l’analyse de la covariance. Les données représentent les moyennes de parcelles, basées sur quarante observations de la hauteur initiale (x) et de la hauteur atteinte après quatre mois (y) de trois variétés de Leucaena leucocephala, chacune étant cultivée dans 10 parcelles d’une station expérimentale.

Tableau 3.15. Hauteur initiale (x) et hauteur quatre mois plus tard (y), en cm, de trois variétés de Leucaena leucocephala), sur une station expérimentale.

L’analyse se fait suivant le modèle du Tableau 3.14. Les calculs sont expliqués ci-dessous:

*Etape 1. Calculer, à l’aide des équations (3.38) à (3.45), la somme des carrés des variables x et y.

C.F.(y) = = 812136.5333

SSTO(y) = (145)² + (149)² + . . . + (184)² - 812136.5333

= 7493.4667

SSG(y) =

= 4328.4667

SSE(y) = 7493.4667 - 4328.4667

= 3615.0

C.F.(x) =

= 20856.0333

SSTO(x) = (18)² + (22)² + . . . + (32)² -20.856.0333

= 966.9697

SSG(x) =

= 539.267

SSE(x) = 966.9697-539.267

= 427.7027

*Etape 2. Calculer la somme des produits des variables x et y à l’aide des équations (3.46) à (3.49).

= 130145.8667

SPTO(xy) = 18(145) + 22(149) + . . . +32(184) -130145.8667

= 2407.1333

SPG(xy) =

= 1506.44

SPE(xy) = 2407.1333 - 1506.44 = 900.6933

*Etape 3. Calculer le coefficient de régression et tester sa signification avec les équations (3.50) et (3.51).

=

= 2.1059

La signification de peut être testée à l’aide du test F. Le critère statistique F est donné par l’équation (3.51).

F =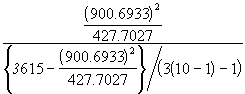

=

= 28.7012

La valeur tabulaire de F correspondant à (1,26) degrés de liberté est égale à 9.41 au seuil de signification de 5%. Ici, la valeur calculée de F est supérieure à la valeur tabulaire, par conséquent diffère de zéro de manière significative.

*Etape 4. Calculer les sommes ajustées des carrés relatives aux différentes sources dans l’analyse de covariance à l’aide des équations (3.52) à (3.54). Synthétiser les résultats comme dans le Tableau 3.14 et calculer les valeurs des carrés moyens des groupes (MSG) et des erreurs (MSE), ainsi que la valeur de F basée sur ces carrés moyens.

SSTO Aj. (y) =

= 1501.2513

SSE Aj. (y) =

= 1268.2422

SSG Aj. (y) = 1501.2513 - 1268.2422

= 233.0091

MSG = = 116.5046

MSE =

= 48.7785

=

= 2.39

Tableau 3.16. Table d’analyse de la covariance des données du Tableau 3.15.

La valeur de F correspondant à (2,26) degrés de liberté au seuil de signification de 5% est 3.37. Puisque la valeur observée de F ( 2.4) est inférieure à la valeur critique, on conclut qu’il n’y a pas de différence significative entre les variétés.

*Etape 5. Trouver les moyennes ajustées de chaque groupe et l’erreur–type de la différence entre les moyennes ajustées de deux groupes quelconques avec les équations (3.55) and (3.57).

= 149.5 - 2.1059(21.6 - 26.37) = 159.54

= 165.2 - 2.1059(25.6 - 26.37) = 166.82

= 178.9 - 2.1059(31.2 - 26.37) = 168.73

SE(d) =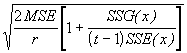

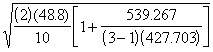= = 3.9891

L’erreur-type de la différence entre les moyennes des groupes peut être utile dans la comparaison par paire des moyennes des groupes, comme on le verra dans le Chapitre 4.

3.11. Analyse de mesures répétées

Les mesures répétées d’unités d’observations sont très fréquentes en recherche forestière. Le terme « répétées » signifie que les mesures sont effectuées sur le même caractère et sur un même échantillon d’observation, mais sont relevées à plusieurs reprises. Dans les études longitudinales, les individus peuvent être suivis sur une période de temps pour enregistrer les changements qui surviennent dans leur état. Parmi les exemples classiques, on peut citer les mesures périodiques du diamètre ou de la hauteur des arbres dans une expérience sylvicole, ou les observations de l’évolution des maladies sur un ensemble de plantules, dans un essai en pépinière. Les mesures répétées peuvent être spatiales plutôt que temporelles. Prenons pour exemple les mesures des caractéristiques du bois de plusieurs troncs dans leur partie basse, centrale et haute, chaque ensemble de troncs appartenant à une espèce différente. Les propriétés du sol observées à partir de multiples carottes de sondage, à des profondeurs de 0-15, 15-50 et de 50-100 cm, dans différents types de végétation sont un autre exemple.

Les mesures répétées se caractérisent principalement par le fait qu’il peut exister une corrélation entre les mesures successives dans l’espace ou dans le temps. L’autocorrélation entre les résidus découlant de mesures répétées sur les mêmes unités expérimentales contredit l’hypothèse fondamentale de l’indépendance des erreurs, sur laquelle se fonde une analyse de variance ordinaire. Toutefois on dispose de plusieurs méthodes pour analyser des mesures répétées. Ces méthodes sont plus ou moins efficaces ou appropriées suivant la nature des données. Si la variance des erreurs reste la même à chacune des mesures successives, et si en outre les covariances entre les erreurs des différentes mesures sont les mêmes, on peut choisir de soumettre les données à une "analyse de modèle mixte à une variable". Si les erreurs ne sont pas structurées, il est préférable d’effectuer une analyse multivariable en prenant des mesures répétées des différents caractères observés sur les mêmes entités (Crowder et Hand, 1990). Nous allons illustrer ci-après les détails d’une analyse à une variable dans un contexte d’observation simplifié et conseillons à nos lecteurs de se référer à (Crowder and Hand, 1990) pour une analyse multivariable dans ce contexte.

Ici, la situation se présente comme suit: on a n individus x p occasions, les individus étant répartis en t groupes de tailles n_i (i = 1, 2, …, t). L’hypothèse à tester implique une comparaison entre les groupes. Le modèle utilisé est le suivant 

y_ijk = m + a _i+ e_ij + b _j + g _ij + e_ijk (3.58)

où y_ijk est l’observation sur le k-ème individu dans le i-ème groupe à la j-ème occasion;

( i =1, …, t, j =1, …, p, k =1, …, n_i.)

m est la moyenne générale,

a _i est l’effet du i-ème niveau du facteur ‘groupe’,

b _j est l’effet du j-ìème niveau du facteur ‘occasion’,

g _ij est l’effet d’interaction pour le i-ème niveau du facteur ‘groupe’ et le j-ème niveau du facteur ‘occasion’. Ce terme mesure les différences entre les types de réponses des groupes, au fil des occasions. Cette interaction sera examinée plus en détail au Chapitre 4.

Dans le modèle (3.58), les composantes aléatoires e_ij et les composantes d’erreurs aléatoires e_ijk sont supposées suivre des lois de distribution indépendantes et normales avec une moyenne nulle et une variance et respectivement. En outre, les a _i et les b _j sont supposés fixes.

Notons y_i.. le total de toutes les observations au niveau i du facteur groupe; y_.j. le total de toutes les observations au niveau j du facteur occasion; y_ij. le total de toutes les observations appartenant à la (ij)-ème cellule; y_… le total général de toutes les observations. Mathématiquement, ces notations s’expriment comme suit

y_i.. = , y_.j. = , y_ij. = , y_… =

Le modèle mixte à une variable d’analyse de variance est illustré ci-dessous.

Tableau 3.17. Représentation schématique du modèle mixte à une variable d’analyse de variance.

Les sommes des carrés du tableau ci-dessus se calculent avec les formules suivantes,

SSTO = (3.59)

SSG =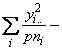 (3.60)

SSE_a = 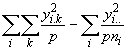(3.61)

SSO =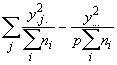 (3.62)

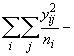
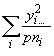
SSOG = 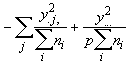(3.63)

SSE_b = SST - SSG - SSE_a - SSO - SSOG (3.64)

Nous illustrerons cette analyse à l’aide des données du Tableau 3.18, sur la croissance mycélienne (en mm) de cinq isolats de Rizoctonia solani sur milieu de gélose dextrosée à base de fécule de pomme de terre au bout de 14, 22, 30 et 38 heures d’incubation, chaque isolat étant cultivé dans trois unités du milieu de culture. Ici, les isolats sont les « groupes » et les différents moments sont les « occasions » dont il est question dans le Tableau 3.17.

Tableau 3.18. Données sur la croissance mycélienne (en mm) de cinq groupes d’isolats de R. solani , sur milieu de culture de gélose dextrosée à base de fécule de pomme de terre (PDA).

L’analyse de ces données peut être conduite comme suit:

*Etape 1. Calculer, à l’aide de l’équation (3.59), la somme totale des carrés des valeurs du

Tableau 3.18.

SSTO =

*Etape 2. Dresser un tableau à double entrée des totaux Isolat x unité de PDA, en additionnant les observations correspondant aux différentes occasions et calculer les totaux marginaux, comme indiqué dans le Tableau 3.19. Calculer SSG et SSE_a en utilisant les valeurs indiquées dans le Tableau et les équations (3.60) et (3.61).

Tableau 3.19. Totaux Isolat x unité de PDA calculés à partir des données du Tableau 3.18.

SSG =

= 4041.04

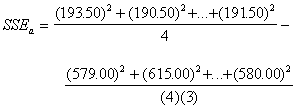
= 81.92

*Etape 3. Dresser le tableau à double entrée des totaux Isolat x Occasion et calculer les totaux marginaux comme indiqué dans le Tableau 3.20. Calculer SSO, SSOG et SSE_b à l’aide des équations (3.62) à (3.64).

Tableau 3.20. Tableau des to totaux Isolat x Occasion calculés à partir des données du Tableau 3.18

SSO =

= 10637.08

SSOG =

= 172.46

SSE_b =

= 29.08

*Etape 4. Faire la synthèse des résultats comme dans le Tableau 3.21 et effectuer les calculs restants pour obtenir les carrés moyens et les rapports F, en utilisant les équations reportées dans le Tableau 3.17.

Tableau 3.21. Tableau de l’analyse de variance des données du Tableau 3.18.

Comparer les valeurs calculées de F avec les valeurs tabulaires de F aux degrés de liberté correspondants, au seuil de probabilité souhaité. Toutes les valeurs calculées de F données dans le tableau ci-dessus sont supérieures aux valeurs tabulaires correspondantes de F. On en déduit que la variation due aux groupes, à l’occasion et leur interaction sont significatives, ce qui signifie que le mode de croissance des isolats diffère au fil du temps.