4. PLAN ET ANALYSE D’EXPERIENCES

On appelle plan et analyse d’expérience l’opération consistant à planifier une expérience pour obtenir des données appropriées et en tirer des conclusions sur tout problème soumis à l’examen. Cette opération peut partir de la formulation, en termes clairs, des objectifs de l’expérience et s’achever par la rédaction des rapports contenant les conclusions importantes de l’enquête. Elle comprend aussi une phase intermédiaire durant laquelle sont définis les détails de l’expérience, notamment la structuration des variables dépendantes et indépendantes, leurs niveaux dans l’expérience, le type de matériel expérimental qui sera utilisé, la méthode de manipulation des variables du matériel expérimental, des techniques d’inférence statistique efficaces et rationnelles etc…

La majorité des expériences reposent sur trois principes fondamentaux, à savoir randomisation, répétition et contrôle local. D’une certaine façon, ces trois principes se complètent mutuellement, puisqu’ils tentent d’augmenter la précision de l’expérience et de garantir la validité du test de signification, tout en conservant, dans toute l’expérience les caractéristiques propres à leurs rôles. Avant de passer à un examen plus approfondi de ces trois principes, nous allons tenter d’expliquer certains termes génériques de la théorie des plans d’expérience, ainsi que la nature de la variation entre les observations faites dans une expérience.

Avant de réaliser une expérience, il convient de définir une unité expérimentale. Celle-ci peut par exemple être constituée d’une feuille, d’un arbre ou d’un groupe d’arbres adjacents. Une unité expérimentale est aussi parfois appelée parcelle. Un groupe de parcelles est appelé bloc. Les observations faites sur les unités expérimentales se caractérisent par de grandes variations, en partie produites par la manipulation de certaines variables, généralement appelées traitements, qui sont inhérentes à l’expérience et manipulées à dessein pour étudier leurs influences. Par exemple, les clones dans les tests clonaux, les doses et les types d’engrais dans les essais sur les engrais etc… peuvent être appelés traitements. En plus de ces variations de source connue, il en existe d’autres dont on ignore l’origine, ou la cause, comme par exemple la variation non contrôlée de facteurs externes liés à l’environnement, les variations génétiques du matériel expérimental, autres que celles dues aux traitements, etc… Ces variations sont inévitables et inhérentes au processus même de l’expérimentation. En raison de leurs influences indésirables, elles ont reçu le nom d’erreurs expérimentales, ce qui signifie qu’il ne s’agit pas d’erreurs arithmétiques, mais de variations dues à une combinaison de facteurs sur lesquels l’expérimentateur ne peut pas agir.

De plus, il est intéressant de noter que ces erreurs introduites par des facteurs externes dans les observations expérimentales peuvent avoir une incidence systématique ou aléatoire. Les erreurs imputables à un équipement défectueux, comme un tendeur de chaîne qui aurait perdu son étalonnage à force d’être utilisé, ou l’erreur due à la fatigue de l’observateur sont des exemples d’erreur systématique. En revanche, la variation imprévisible de la quantité de feuilles ramassées dans un collecteur de litière, dans le cadre d’un traitement particulier d’une expérience liée, est de caractère aléatoire, ou fortuit. Il est clair que quel que soit le nombre de fois où l’on répètera les mesures, l’erreur systématique subsistera, alors que les erreurs aléatoires finissent le plus souvent par disparaître à l’issue de mesures répétées. Les trois principes de base, à savoir randomisation, répétition et contrôle local, permettent d’ éviter l’erreur systématique et de limiter l’erreur aléatoire.

On appelle randomisation la technique d’attribution des traitements, ou des facteurs à tester, aux unités expérimentales conformément à des lois ou probabilités définies. C’est la randomisation dans son sens technique strict, qui garantit l’élimination des erreurs systématiques et le caractère purement aléatoire de tout élément d’erreur persistant dans les observations. A partir de là, on peut faire une estimation valable des fluctuations aléatoires, indispensable pour tester la signification de différences réelles.

Grâce à la randomisation, chaque unité expérimentale aura une chance égale de recevoir un traitement quelconque. Si, par exemple, cinq clones d’eucalyptus doivent être testés dans 25 parcelles, la randomisation garantit que certains clones ne seront pas favorisés ou pénalisés par des sources de variation externes qui ne dépendent pas de l’action, délibérée ou non, de l’expérimentateur. Le processus d’allocation aléatoire peut se faire de plusieurs façons, par tirage au sort ou en tirant des nombres d’une page, choisie au hasard, de nombres aléatoires. La méthode est illustrée dans les sections qui suivent sur les différents types de plans expérimentaux.

Par répétition, on entend la répétition d’une expérience dans des conditions identiques. Dans le contexte des plans d’expérience, en revanche, le terme se réfère au nombre d’unités expérimentales distinctes faisant l’objet du même traitement. La répétition, conjuguée à la randomisation, fournira une base pour estimer la variance des écarts. Sans la randomisation, un nombre quelconque de répétitions pourrait ne pas déboucher sur une estimation réelle de l’erreur. Plus le nombre de répétitions est grand, plus la précision de l’expérience est grande.

Le nombre de répétitions que doit comporter une expérience quelconque dépend de nombreux facteurs, notamment de l’homogénéité du matériel expérimental, du nombre de traitements, du degré de précision requis etc… En règle général, on pourrait postuler que le nombre de répétitions dans un plan doit fournir au moins dix à quinze degrés de liberté, pour calculer la variance de l’erreur expérimentale.

On entend par contrôle local le contrôle de tous les facteurs autres que ceux sur lesquels portent les recherches. Comme la répétition, le contrôle local est un dispositif visant à réduire ou à maîtriser la variation due à des facteurs externes et à accroître la précision de l’expérience. Si, par exemple, un champ d’essais est hétérogène, du point de vue de la fertilité du sol, il peut être divisé en blocs plus petits de façon à ce que les parcelles se trouvant à l’intérieur de chaque bloc tendent à être plus homogènes. Ce type d’homogénéité des parcelles (unités expérimentales) garantit une comparaison non biaisée des moyennes des traitements. En effet, il serait difficile de dire que la différence moyenne entre deux traitements provient uniquement de différences entre eux, s’il restait aussi des différences entre les parcelles. Ce type de contrôle local visant à rendre homogènes des unités expérimentales, augmentera la précision de l’expérience et aidera à tirer des conclusions valides.

Pour résumer, on peut dire qu’alors que la randomisation vise à éliminer une erreur systématique (ou biais) dans l’allocation et, partant, à ne laisser qu’un élément de variation d’erreur aléatoire, les deux autres méthodes, à savoir la répétition et le contrôle local, tentent de maintenir cette erreur aléatoire à un niveau aussi faible que possible. Les trois principes sont cependant essentiels pour faire une estimation valable de la variance de l’erreur et garantir la validité du test de signification.

Dans un plan expérimental entièrement randomisé (PER), les traitements sont attribués complètement au hasard de sorte que chaque unité expérimentale a la même chance de recevoir un traitement donné quel qu’il soit. Dans un PER, toute différence entre les unités expérimentales soumises au même traitement est considérée comme une erreur expérimentale. En conséquence, le PER n’est approprié que pour les expériences ayant des unités expérimentales homogènes, telles que les essais en laboratoire, dans lesquelles il est relativement facile de maîtriser les effets dus à l’environnement. Le PER est rarement utilisé pour les essais en champs, où il existe une grande variation entre les parcelles expérimentales, par exemple au niveau de facteurs comme les sols. .

Nous allons maintenant présenter la procédure par étapes de la randomisation ainsi que le schéma d’un PER, pour un essai de culture en pots comportant quatre traitements A, B, C et D, répétés cinq fois .

*Etape 1. Déterminer le nombre total de parcelles expérimentales (n), comme produit du nombre de traitements (t) et du nombre de répétitions (r); c’est-à-dire, n = rt. Dans notre exemple, n = 5 x 4 = 20. Dans ce cas, un pot contenant une seule plante sera considéré comme une parcelle. Si le nombre de répétitions n’est pas le même pour tous les traitements, on obtiendra le nombre total de pots expérimentaux en faisant la somme des répétitions de chaque traitement :

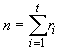où r_i est le nombre de répétitions du ième traitement

*Etape 2. Attribuer un numéro à chaque parcelle expérimentale, selon une quelconque méthode appropriée, par exemple, en utilisant des suites de chiffres de 1 à n.

*Etape 3. Allouer au hasard les traitements aux parcelles expérimentales, en utilisant une table de nombres aléatoires de la manière suivante. Tirer un point de départ dans une table de nombres aléatoires (voir Annexe 6), en pointant le doigt sur un endroit quelconque de la page, les yeux fermés. En l’espèce, nous supposerons que le point de départ est tombé à l’intersection du sixième rang et de la douzième colonne de nombres à deux chiffres. A partir de ce point de départ, lire la colonne en descendant pour obtenir n = 20 nombres aléatoires différents à deux chiffres. Dans notre exemple, en partant de l’intersection du sixième rang et de la douzième colonne, ces 20 nombres sont indiqués ci-dessous, avec leur ordre d’apparition.

Nombre aléatoire : 37, 80, 76, 02, 65, 27, 54, 77, 48, 73,

Ordre d’apparition : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,

Nombre aléatoire : 86, 30, 67, 05, 50, 31, 04, 18, 41, 89

Ordre d’apparition : 11, 12, 13, 14, 15, 16, 17, 18, 19, 20

Rangez les n nombre aléatoires obtenus par ordre croissant ou décroissant. Dans notre exemple, les 20 nombres aléatoires sont rangés du plus petit au plus grand, comme indiqué dans le tableau suivant :

Diviser les n rangs obtenus en t groupes, contenant chacun r nombres, suivant l’ordre dans lequel sont apparus les nombres aléatoires. Dans notre exemple, les 20 rangs sont divisés en quatre groupes, dont chacun est constitué de cinq nombres :

Allouez les t traitements aux n parcelles expérimentales, en prenant le numéro du groupe comme numéro de traitement et les rangs correspondants dans chaque groupe comme le nombre de parcelles auxquelles le traitement correspondant sera alloué. Dans notre exemple, le premier groupe est assigné au traitement A et les parcelles numéro 8, 13, 10, 14 et 2 sont désignées pour recevoir ce traitement ; le deuxième groupe est assigné au traitement B, avec les parcelles numéro 18, 5, 15, 3 et 4 ; le troisième groupe est assigné au traitement C, avec les parcelles numéro 16, 12, 19, 11 et 9 ; et le quatrième groupe est assigné au traitement D avec les parcelles numéro 1, 17, 6, 7 et 20. Le schéma définitif de l’expérience est illustré à la Figure 4.1.

Figure 4.1. Schéma-type d’un plan d’expérience entièrement randomisé, comportant quatre traitements (A, B, C et D), répétés cinq fois.

Il existe deux sources de variation entre les n observations tirées d’un essai de PER. L’une est la variation due aux traitements et l’autre est l’erreur expérimentale. Leur taille relative indique si la différence observée entre les traitements est réelle ou si elle est due au hasard. La différence due au traitement est " réelle " si elle dépasse dans une mesure significative l’erreur expérimentale.

L’un des avantages majeurs d’un PER est que son analyse de variance se calcule facilement, surtout si le nombre de répétitions n’est pas uniforme pour tous les traitements. Pour la plupart des autres plans, l’analyse de variance se complique lorsque la perte de données dans certaines parcelles entraîne des disparités dans les répétitions des traitements testés.

Nous allons voir ci-dessous les étapes de l’analyse de variance des données provenant d’une expérimentation relative à un PER comportant un nombre de répétitions non uniforme. Les formules peuvent être adaptées facilement en cas de répétitions égales, de sorte qu’elles ne sont pas décrites à part. Pour illustrer cette démonstration, on a utilisé des données provenant d’un essai en laboratoire, dans lequel les observations portaient sur la croissance du mycelium de différents isolats de Rizoctonia solani, sur milieu de culture PDA (Tableau 4.1).

*Etape 1. Regrouper les données par traitements et calculer les totaux des traitements (T_i) et le total général (G). Les résultats de notre exemple sont indiqués dans le Tableau 4.1.

*Etape 2. Dresser un Tableau d’analyse de variance, suivant le modèle du Tableau 4.2

Tableau 4.1. Croissance du mycélium, en diamètre (mm), de la colonie d’isolats de R. solani, sur milieu de culture PDA, après 14 heures d’incubation

Tableau 4.2. Schéma de l’analyse de variance d’un PER, avec répétitions inégales

*Etape 3. Avec les totaux des traitements (T_i) et le total général (G) du Tableau 4.1, calculer comme suit le facteur de correction et les différentes sommes des carrés. Supposons que y_ij représente l’observation du jème milieu PDA appartenant au ième isolat; i = 1, 2, …, t ; j = 1, 2, …, r_i..

(4.1)

= 15301.23

(4.2)

=

= 789.27

SST = 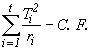(4.3)

=

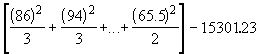
= 762.69

SSE = SSTO - SST (4.4)

= 789.27 - 762.69 = 26.58

*Etape 4. Entrer toutes les valeurs des sommes des carrés dans le tableau d’analyse de la variance et calculer les carrés moyens et la valeur de F comme indiqué dans le Tableau 4.2

*Etape 5. Prendre dans l’Annexe 3 les valeurs tabulaires de F, avec f₁ et f₂ degrés de liberté, où f₁ = df du traitement = (t - 1) et f₂ = df de l’erreur = (n – t), respectivement. Dans notre exemple, la valeur tabulaire de F, avec f₁ = 4 et f₂ = 8 degrés de liberté est de 3.84, au seuil de signification de 5%. Ces résultats sont consignés dans le Tableau 4.3.

Tableau 4.3. Analyse de la variance des données du Tableau 4.1 sur la croissance du mycélium.

* Significatif au seuil de 5%

*Etape 6. Comparer la valeur calculée de F de l’Etape 4 avec la valeur tabulée de F de l’Etape 5, et déterminez si la différence entre les traitements est significative, d’après les règles ci-après :

i) Si la valeur calculée de F est supérieure à sa valeur tabulaire au seuil de signification de 5%, la variation due aux traitements est dite significative, ce qui est généralement indiqué par un astérisque au-dessus de la valeur calculée de F, dans l’analyse de variance.

ii) Si la valeur calculée de F est inférieure ou égale à la valeur tabulaire de F au seuil de signification de 5%, la variation due aux traitements est dite non significative, ce qui est indiqué par la mention ns au-dessus de la valeur calculée de F (ou par l’absence d’indication au-dessus de cette valeur).

Une valeur non significative de F dans l’analyse de variance indique que l’expérience n’a pas réussi à détecter de différence entre les traitements. Elle ne prouve en aucun cas que tous les traitements sont les mêmes car la non détection d’une différence entre les traitements, attestée par une valeur non significative du critère F, pourrait s’expliquer par une différence nulle ou minime, ou par une erreur expérimentale importante, ou encore par ces deux facteurs. Ainsi, dans tous les cas où la valeur de F n’est pas significative, le chercheur devrait examiner l’ampleur de l’erreur expérimentale et les différences numériques entre les moyennes des traitements. Si ces deux valeurs sont grandes, il est conseillé de refaire l’essai et de tenter de réduire l’erreur expérimentale pour que les éventuelles différences entre les traitements puissent être détectées. En revanche, si les deux valeurs sont petites, les différences entre les traitements sont probablement trop faibles pour avoir une signification économique, si bien qu’il n’est pas nécessaire de faire de nouveaux essais.

Dans notre exemple, la valeur calculée de F (57.38) est supérieure à sa valeur tabulaire (3.84) au seuil de signification de 5%. Les différences entre les traitements sont donc significatives. En d’autres termes, les probabilités que toutes les différences observées entre les cinq moyennes des traitements soient dues au hasard sont inférieures à 5 pour cent. On notera qu’une valeur significative de F confirme l’existence de quelques différences entre les traitements testés, mais ne précise pas pour quelle(s) paire(s) de traitements spécifiques la différence est significative. Ces informations s’obtiennent grâce aux procédures de comparaison des moyennes examinées dans la Section 4.2.3.

*Etape 7. Calculer comme suit la moyenne générale et le coefficient de variation (cv):

Moyenne générale = (4.5)

cv = (4.6)

Dans notre exemple,

Moyenne générale =

cv =

Le cv affecte le degré de précision des comparaisons entre les traitements et donne une bonne indication de la fiabilité de l’expérience. C’est une expression de l’erreur expérimentale totale, en pourcentage de la moyenne totale ; Ainsi, plus la valeur de cv est grande, moins l’expérience est fiable. Le cv varie considérablement suivant le type d’expérience, la plante cultivée, et les caractères mesurés. Toutefois, un chercheur expérimenté peut relativement bien juger de l’acceptabilité d’une valeur spécifique du cv pour un type d’expérience donné. Les résultats d’expériences donnant un cv supérieur à 30% sont sujets à caution.

Dans le domaine de la recherche forestière, l’une des procédures les plus couramment employées, pour les comparaisons appariées est le test de la plus petite différence significative (PPDS). D’autres méthodes, comme le test de Duncan, le test de la différence raisonnablement significative et le test de Student-Newman-Keuls sont décrites dans Gomez et Gomez (1980), Steel et Torrie (1980) et Snedecor et Cochran (1980). Le test PPDS est décrit dans la présente section.

Le test PPDS est la procédure la plus simple pour comparer des paires. Cette procédure fournit une valeur unique de la PPDS qui, à un niveau de signification déterminé, marque la limite entre la différence significative et non significative entre une paire de moyennes de traitements quelconque. Deux traitements présentent donc des différences significatives à un seuil de signification prescrit si leur différence est supérieure à la valeur calculée de la PPDS. Dans le cas contraire, leurs différences sont considérées comme non significatives.

Si le test PPDS est tout à fait approprié pour les plans de comparaisons appariées, il ne permet pas de comparer toutes les paires de moyennes possibles, surtout si le nombre de traitements est grand. En effet, le nombre de paires de moyennes de traitements possibles augmente rapidement avec le nombre de traitements. La probabilité qu’au moins une paire ait une différence supérieure à la valeur de la PPDS, et uniquement due au hasard, augmente avec le nombre de traitements testés. Par exemple, dans les expériences où il n’existe pas de différence réelle entre toutes les traitements, il est possible de démontrer que la différence numérique entre la plus grande et la plus petite moyenne des traitements devrait être supérieure à la valeur de la PPDS, au seuil de signification de 5%, 29 fois sur cent dans le cas de 5 traitements, 63 fois sur cent dans le cas de 10 traitements, et 83 fois sur cent dans le cas de 15 traitements. On évitera donc de recourir au test PPDS pour comparer toutes les paires de moyennes possibles. Dans les cas où ce test s’applique, on ne l’utilisera que si le critère F relatif à l’effet des traitements est significatif et si le nombre de traitements n’est pas trop élevé (inférieur à six).

La procédure d’application du test PPDS pour comparer deux traitements quelconques – par exemple le traitement i et le traitement j, se déroule en plusieurs étapes :

*Etape 1. Calculer la différence moyenne entre le traitement i et le traitement j :

(4.7)

où sont les moyennes des traitements i et j.

*Etape 2. Calculer la valeur de la PPDS, au seuil de signification :

(4.8)

où est l’erreur-type de la différence moyenne et est la valeur t de la distribution de Student, extraite de l’Annexe 2, au seuil de signification et pour v = degrés de liberté de l’erreur.

*Etape 3. Comparer la différence moyenne calculée au cours de l’étape 1 avec la valeur de la PPDS calculée au cours de l’étape 2. Si la valeur absolue de dij est supérieure à la valeur de la PPDS, conclure que les différences entre les traitements i et j sont significatives au seuil de signification ,.

Lorsque l’on applique cette procédure, il est important d’identifier l’erreur-type appropriée de la différence moyenne (), applicable à la paire de traitements que l’on veut comparer. La méthode varie en fonction du plan d’expérience utilisé, du nombre de répétitions des deux traitements soumis à la comparaison et du type spécifique de moyennes que l’on comparera. Dans le cas d’un PER, lorsque les deux traitements n’ont pas le même nombre de répétitions, se calcule comme suit:

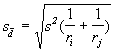(4.9)

où r_i et r_j représentent le nombre de répétitions des traitements i et j , et s² la moyenne des carrés des erreurs dans l’analyse de variance.

Nous illustrerons ceci par un exemple, à l’aide des données du Tableau 4.1. Le chercheur veut comparer les cinq isolats de R. solani, en particulier la croissance de leur mycélium sur milieu PDA. Pour appliquer le test PPDS, on procèdera par étapes, de la manière suivante :

*Etape 1. Calculer la différence moyenne entre chaque paire de traitements (isolats) comme indiqué dans le Tableau 4.4.

*Etape 2. Calculer la valeur de la PPDS, au seuil de signification a . Etant donné que certains traitements sont répétés trois fois et d’autres deux fois, il faut calculer trois ensembles de valeurs de la PPDS.

Pour comparer deux traitements comportant chacun trois répétitions, la valeur de la PPDS se calcule comme suit.

où la valeur de s² = 3.32 est dérivée du Tableau 4.3 et la valeur de la distribution de Student t (2.31), pour 8 degrés de liberté, au seuil de signification de 5% est extraite de l’Annexe 2.

Pour comparer deux traitements répétés trois fois chacun, calculer la valeur de la PPDS, comme suit :

Pour comparer deux traitements dont un est répété deux fois et l’autre trois fois, la valeur de la PPDS est

= 3.84 mm

*Etape 3. Comparer la différence entre chaque paire de traitements calculée à l’Etape 1 aux valeurs correspondantes de la PPDS calculées à l’étape 2, et placer la notation appropriée (astérisque, ns ou absence d’indication). Par exemple, la différence moyenne entre le premier traitement (comportant trois répétitions) et le deuxième traitement (trois répétitions) est de 2.66 mm. Etant donné que la différence moyenne est inférieure à la valeur de la PPDS correspondante (3.44 mm), elle est non significative au seuil de signification de 5%. Par ailleurs, la différence moyenne entre le premier traitement (trois répétitions) et le deuxième (deux répétitions) est de 4.05 mm. Etant donné que la différence moyenne est supérieure à la valeur de la PPDS correspondante (3.84), elle est significative au seuil de 5%, ce que l’on indiquera par un astérisque. Les résultats du test, pour toutes les paires de traitements, sont indiqués dans le Tableau 4.4.

Tableau 4.4. Comparaison entre le diamètre moyen (en mm) de chaque paire de traitements, à l’aide du test PPDS, avec des répétitions non uniformes, pour les données du Tableau 4.1.

* Significative au seuil de 5%

Note: Les valeurs indiquées entre parenthèses sont les valeurs de la PPDS

Avant de passer à la section suivante, nous mentionnerons un point qui peut être utile pour déterminer le nombre de répétitions à pratiquer pour qu’une expérience soit " raisonnablement " fiable. Le principe est que le nombre de répétitions doit être tel que les degrés de liberté de l’erreur soient de l’ordre de 12. En effet, les valeurs critiques dérivées de certaines distributions, notamment des lois de Student ou des distributions de F, se stabilisent pratiquement après 12 degrés de liberté, ce qui confère une certaine stabilité aux conclusions tirées de ces expériences. Par exemple, si l’on planifie un PER dans lequel les traitements t sont répétés un nombre de fois égal, on identifiera le df de l’erreur de t(r-1) à 12 et on calculera r pour des valeurs connues de t. Des stratégies similaires peuvent être suivies pour de nombreux autres plans qui sont expliqués dans les sections suivantes.

Le plan expérimental en blocs aléatoires complets (PEBAC) est l’un des dispositifs les plus largement utilisés en recherche forestière. Il se prête généralement à des expériences en champs dans lesquels le nombre de traitements est peu important et où il existe un facteur évident pouvant servir de base pour identifier des ensembles homogènes d’unités expérimentales. Le PEBAC se caractérise principalement par la présence de blocs de taille égale, dont chacun contient tous les traitements.

Cette technique a pour but de réduire l’erreur expérimentale en éliminant la contribution de sources connues de variation entre les unités expérimentales. Pour ce faire, on regroupe les unités expérimentales en blocs de manière à minimiser la variabilité à l’intérieur de chaque bloc et à maximiser la variabilité entre les blocs. Etant donné que seule la variation à l’intérieur d’un bloc devient un élément de l’erreur expérimentale, le dispositif par blocs est particulièrement efficace lorsque le type de variabilité du secteur d’expérimentation est prévisible.

Dans un dispositif par blocs, l’idéal est d’utiliser une source de variation grande et hautement prévisible, telle que l’hétérogénéité du sol, dans un essai d’engrais ou de provenance dans lequel le rendement est le principal caractère sur lequel on cherche à obtenir des informations. Dans le cas d’expériences de ce genre, après avoir identifié la source spécifique de variabilité qui servira de critère pour les blocs, il faut choisir la taille et la forme des blocs pour maximiser la variabilité entre ceux-ci. Les principes directeurs de cette décision sont les suivants : i) si le gradient est unidirectionnel (c’est-à-dire s’il y a un seul gradient), les blocs seront longs et étroits, et orientés de façon à ce que leur longueur soit perpendiculaire à la direction du gradient ; ii) si le gradient de fertilité va dans deux directions, avec un gradient beaucoup plus fort que l’autre, on ignorera le plus faible et l’on suivra les directives qui viennent d’être données pour le gradient unidirectionnel ; iii) si le gradient de fertilité va dans deux directions, et si les deux gradients ont la même force et sont perpendiculaires l’un par rapport à l’autre, on choisira des blocs aussi carrés que possible ou d’autres types de plans comme le carré latin (Gomez et Gomez, 1980).

Si l’on utilise cette technique, la définition des blocs et l’objet de leur utilisation doivent être compatibles tout au long de l’expérience. Cela signifie que dans tous les cas où il existe une source de variation sur laquelle le chercheur ne peut pas agir, on veillera à ce que cette variation se produise entre des blocs plutôt qu’à l’intérieur d’un même bloc. Par exemple, s’il est impossible de mener à leur terme en un seul jour certaines opérations comme l’application d’insecticides ou la collecte de données, pour toute l’expérience, celles-ci devront être achevées en une journée sur toutes les parcelles d’un même bloc. De cette manière, la variation entre les jours (qui peut être renforcée par des facteurs météorologiques) devient un élément de la variation du bloc et se trouve par conséquent exclue de l’erreur expérimentale. Si, dans le cadre de l’essai, plusieurs chercheurs doivent prendre des mesures, le même observateur sera chargé de prendre des mesures sur toutes les parcelles d’un même bloc. Ainsi, l’éventuelle variation entre les observateurs constituera un élément de la variation du bloc et non de l’erreur expérimentale.

Le processus de randomisation d’un PEBAC est appliqué à chaque bloc de manière séparée et indépendante. Nous allons illustrer la marche à suivre pour une expérience en champ comportant six traitements A, B, C, D, E, F et trois répétitions.

*Etape 1. Diviser la surface expérimentale en r blocs égaux, r étant le nombre de répétitions, suivant la technique des blocs décrite dans la Section 4.3.1. Dans notre exemple, la surface expérimentale est divisée en trois blocs, comme dans la Figure 4.2. Nous supposerons qu’il y a un gradient de fertilité unidirectionnel sur le côté long du champ d’expérimentation, de sorte que le bloc est rectangulaire et perpendiculaire à la direction du gradient.

Figure 4.2. Division d’une surface expérimentale en trois blocs constitués de six parcelles chacun, pour un Plan expérimental en blocs aléatoires complets, comportant six traitements et trois répétitions. Les blocs sont rectangulaires et disposés perpendiculairement à la direction du gradient unidirectionnel (indiqué par une flèche).

*Etape 2. Subdiviser le premier bloc en t parcelles expérimentales, t étant le nombre de traitements. Attribuer aux t parcelles des numéros qui se suivent, allant de 1 à t, et attribuez t traitements au hasard aux t parcelles, suivant l’une des procédures de randomisation applicable au PER décrit dans la Section 4.2.1. Dans notre exemple, le bloc I est subdivisé en six blocs de même taille, dont les numéros se suivent, de haut en bas (Figure 4.3) et les six traitements sont alloués au hasard aux six parcelles, à l’aide de la table des nombres aléatoires.

Figure 4.3. Numérotage des parcelles et allocation aléatoire des six traitements (A, B, C, D, E, et F) aux six parcelles du Bloc I.

*Etape 3. Répéter toute la phase 2 pour chacun des blocs restants. En ce qui concerne notre exemple, la disposition finale est illustrée à la Figure 4.4.

Figure 4.4. Schéma-type d’un plan expérimental en blocs aléatoires complets, avec six traitements (A, B, C, D, E et F) et trois répétitions.

Tout PEBAC a trois sources de variabilité - le traitement, la répétition (ou bloc) et l’erreur expérimentale - soit une de plus qu’un PER, en raison de l’adjonction de la répétition qui correspond à la variabilité entre les blocs.

Nous illustrerons les étapes de l’analyse de la variance applicable à un PEBAC, à l’aide des données d’une expérience consistant à comparer la circonférence à hauteur de poitrine (gbh) d’arbres de huit provenances de Gmelina arborea, six ans après leur plantation (Tableau 4.5).

Tableau 4.5. Gbh moyenne (en cm) des arbres dans des parcelles de différentes provenances de Gmelina arborea, 6 ans après la plantation, dans une expérience en champ relevant d’un PEBAC.

*Etape 1. Regrouper les données par traitement et par répétition et calculer les totaux des traitements, (T_i), des répétitions (R_j) et le total g& eacute;néral (G), comme indiqué dans le Tableau 4.5.

*Etape 2. Dresser le tableau préliminaire de l’analyse de la variance:

Tableau 4.6. Représentation schématique de l’analyse de la variance d’un PEBAC

*Etape 3. Calculer le facteur de correction et les différentes sommes des carrés (SS) mentionnées dans le tableau ci-dessus. Notons y_ij l’observation du i-ème traitement faite dans le jème bloc; i = 1,…,t ; j = 1,…,r.

C F = (4.10)

=

SSTO = (4.11)

=

= 678.42

SSR = 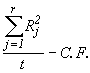(4.12)

= 20989.97

= 110.98

SST = 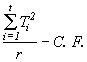(4.13)

=

= 426.45

SSE = SSTO - SSR - SST (4.14)

= 678.42 - 110.98 - 426.45 = 140.98

*Etape 4. A partir des sommes des carrés obtenues, calculer le carré moyen et la valeur de F pour tester les différences des traitements, comme indiqué dans le Tableau 4.6. Les résultats sont reportés dans le Tableau 4.7.

Tableau 4.7 Analyse de la variance des données sur la gbh figurant dans le Tableau 4.5.

*Significative au seuil de 5%

*Etape 5. Extraire les valeurs de F de l’Annexe 3, pour f₁ = df des traitements et f₂ = df de l’erreur. Pour notre exemple, la valeur tabulaire de F pour f₁ = 7 et f₂ = 14 degrés de liberté est de 2.76 au seuil de signification de 5%.

*Etape 6. Comparer la valeur calculée de F de l’étape 4 aux valeurs tabulaires de F de l’étape 5, et déterminer si les différences entre les traitements sont significatives ou non. La valeur calculée de F (6.05) étant supérieure à la valeur tabulaire de F au seuil de signification de 5%, on peut conclure que l’expérience met en évidence l’existence de différences significatives entre les provenances, mesurées par la croissance de leur gbh.

*Etape 7. Calculer le coefficient de variation:

(4.15)

=

La valeur du cv est relativement faible, donc le degré de précision des résultats de l’expérience en champ est acceptable.

Les moyennes des traitements sont comparées selon la méthode décrite pour le PER dans la Section 4.2.3 à l’aide de la formule

(4.16)

où est l’erreur type de la différence entre les moyennes des traitements et où est la valeur tabulaire de t , tirée de l’Annexe 2, au seuil de signification et avec v = degrés de liberté de l’erreur. La quantité se calcule comme suit:

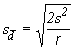(4.17)

où s² est le carré moyen dû à l’erreur et r le nombre de répétitions.

Pour illustrer ceci par un exemple, nous allons poursuivre l’analyse conduite pour les données du Tableau 4.5 et comparer ainsi toutes les paires de traitements possibles à l’aide du test de la PPDS.

*Etape 1. Calculer la différence entre les moyennes des traitements comme indiqué dans le Tableau 4.8.

Tableau 4.8. Différence entre la gbh moyenne (en cm) pour chaque paire de traitements d’après les données du Tableau 4.4.

* Significative au seuil de 5%

*Etape 2. Calculer la valeur de la PPDS au seuil de signification a . Etant donné que tous les traitements sont répétés le même nombre de fois, il suffit de calculer une seule valeur de la PPPDS. Celle-ci s’obtient à l’aide des équations (4.16) et (4.17).

*Etape 3. Comparer la différence entre les moyennes des traitements avec la valeur calculée de la PPDS et marquer d’un astérisque les différences significatives. Les résultats sont reportés dans le Tableau 4.8.

On parle de " données manquantes " dans tous les cas où l’on ne dispose d’observation valide pour aucune des unités expérimentales. Les données manquantes peuvent avoir plusieurs causes : mauvaise application accidentelle des traitements, observations erronées, destruction d’unités expérimentales due à des calamités naturelles comme le feu, les dégâts dus à la faune etc... Il est toutefois primordial d’examiner attentivement ces raisons. La destruction du matériel expérimental ne doit pas être due à l’effet du traitement. Si dans une parcelle aucun arbre n’a survécu, pour des raisons manifestement sans rapport avec les traitements, par exemple parce que la parcelle a été broutée par des animaux errants ou vandalisée par des voleurs, les données manquantes doivent être déclarées comme il convient. En revanche, si dans un essai d’insecticides, par exemple, une parcelle témoin (non traitée) est totalement détruite par des insectes, ce dommage est la conséquence logique de l’absence de traitement. Ainsi, les données correspondantes sur cette parcelle devraient être reconnues comme valides (rendement nul si tous les arbres de la parcelle sont détruits, ou faible si quelques plants ont survécu), et non pas considérées comme manquantes.

L’apparition de données manquantes a deux conséquences majeures : des informations sont perdues et l’analyse de variance standard n’est pas applicable. Lorsqu’une expérience comporte une ou plusieurs observations manquantes, les procédures de calcul standard de l’analyse de variance ne s’appliquent plus, sauf pour le PER. Dans ces situations, il est possible d’utiliser la technique de formulation d’une donnée manquante qui permet d’estimer une observation manquante unique à l’aide d’une formule adaptée au plan d’expérience concerné. Cette estimation est insérée à la place de la donnée manquante et l’ensemble de données ainsi complété est ensuite soumis à l’analyse de variance standard, légèrement modifiée.

On notera que l’estimation d’une donnée manquantes obtenue grâce à cette technique ne donne pas d’information supplémentaire ; aucune manipulation statistique ne permet de récupérer une donnée une fois qu’elle est perdue. L’objet de cette procédure est simplement de permettre au chercheur de faire les calculs habituels de l’analyse de la variance (comme si les données étaient complètes), sans recourir aux procédures plus complexes nécessaires pour des ensembles de données incomplets.

Dans un plan expérimental en blocs aléatoires complets comprenant une seule valeur manquante, celle-ci est estimée par la relation:

(4.18)

où y = estimation de la donnée manquante

t = Nombre de traitements

r = Nombre de répétitions

B₀ = Total des valeurs observées de l a répétition dans laquelle se trouve la donnée manquante

T₀ = Total des valeurs observées du traitement dans lequel se trouve la donnée manquante

G₀ = Total général de toutes les valeurs observées

La donnée manquante est remplacée par la valeur calculée de y et la procédure de calcul habituelle, légèrement modifiée, de l’analyse de variance est appliquée à l’ensemble de données complété.

La procédure est illustrée à l’aide des données du Tableau 4.5. La donnée manquante est supposée être la valeur du sixième traitement (sixième provenance) dans la répétition II (voir Tableau 4.9). Les étapes du calcul de l’analyse de variance et des comparaisons appariées des moyennes de traitements sont les suivantes :

*Etape 1. Estimer la valeur manquante à l’aide de l’équation (4.18) et les valeurs des totaux du Tableau 4.9.

= 26.47

Tableau 4.9. Données du Tableau 4.5, avec une observation manquante

M = donnée manquante

*Etape 2. Remplacer la donnée manquante du Tableau 4.9 par sa valeur estimée, calculée dans l’étape 1, comme indiqué dans le Tableau 4.10 et effectuer l’analyse de variance de l’ensemble de données augmenté, sur la base de la procédure standard de la Section 4.3.3.