


Tableau 4.10. Données du Tableau 4.7 - la donnée manquante est remplacée par la valeur estimée par la technique de formulation de la donnée manquante.
|
Traitement (Provenance) |
Répétition |
Total des traitements |
||
|
Rep. I |
Rep II |
Rep. III |
(T) |
|
|
1 |
30.85 |
38.01 |
35.1 |
103.96 |
|
2 |
30.24 |
28.43 |
35.93 |
94.6 |
|
3 |
30.94 |
31.64 |
34.95 |
97.53 |
|
4 |
29.89 |
29.12 |
36.75 |
95.76 |
|
5 |
21.52 |
24.07 |
20.76 |
66.35 |
|
6 |
25.38 |
26.47a |
32.19 |
84.04 |
|
7 |
22.89 |
19.66 |
26.92 |
69.47 |
|
8 |
29.44 |
24.95 |
37.99 |
92.38 |
|
Total rép. (R) |
221.15 |
222.35 |
260.59 |
|
|
Total général (G) |
704.09 |
|||
a Donnée manquante estimée par la technique de formulation de la donnée manquante
*Etape 3. Apporter les modifications suivantes à l’analyse de variance de l’étape 2; Soustraire 1 du df total et du df de l’erreur. Dans notre exemple, le df total tombe de 23 à 22 et df de l’erreur de 14 à 13. Calculer le facteur de correction du biais (B)
B = 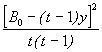 (4.19)
(4.19)
= ![]()
= 2.00
et soustraire la valeur calculée de B ( 2.00) de la somme des carrés des traitements et de la somme totale des carrés. Dans notre exemple, la SSTO et la SST calculées dans l’étape 2 à partir des données augmentées du Tableau 4.10, sont respectivement de 680.12 et de 432.09. En soustrayant la valeur de B ( 2.00) de ces valeurs de SS, on obtient la SST et la SSTO ajustées:
SST ajustée = 432.09 - 2.00
= 430.09
SSTO ajustée = 680.12 - 2.00
= 678.12
L’analyse de la variance ainsi modifiée est reportée dans le Tableau 4.11.
Tableau 4.11. Analyse de la variance des données du Tableau 4.7, avec une valeur manquante estimée par la technique de formulation d’une donnée manquante.
|
Source de |
Degré de liberté |
Somme des carrés |
Carré |
F |
F tabulaire |
|
variation |
moyen |
calculé |
5 % |
||
|
Répétition |
2 |
125.80 |
62.90 |
6.69 |
|
|
Traitement |
7 |
430.09 |
61.44 |
6.53* |
2.83 |
|
Erreur |
13 |
122.23 |
9.40 |
||
|
Total |
22 |
678.12 |
* Significative au seuil de 5%
*Etape 4. Pour les comparaisons par paire de moyennes de traitements, dont l’un contient une donnée manquante, calculer l’erreur-type de la différence moyenne![]() :
:
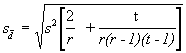 (4.20)
(4.20)
où s2 est le carré moyen de l’erreur fournit par l’analyse de variance de l’étape 3, r le nombre de répétitions et t le nombre de traitements.
Par exemple, pour comparer la moyenne du sixième traitement (auquel manque une donnée) avec celle d’un quelconque autre traitement, ![]() se calcule comme suit :
se calcule comme suit :
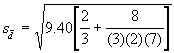 = 2.84
= 2.84
Cette valeur de ![]() peut être utilisée pour calculer les valeurs de la PPDS. La méthode de calcul des valeurs de la PPDS est indiquée ci-dessous. Si l’on prend tv comme valeur tabulaire de t pour 13 df au seuil de signification de 5% (voir Annexe 3), les valeurs de la PPDS servant pour comparer la moyenne du sixième traitement avec toute autre moyenne de traitement se calculent de la manière suivante:
peut être utilisée pour calculer les valeurs de la PPDS. La méthode de calcul des valeurs de la PPDS est indiquée ci-dessous. Si l’on prend tv comme valeur tabulaire de t pour 13 df au seuil de signification de 5% (voir Annexe 3), les valeurs de la PPDS servant pour comparer la moyenne du sixième traitement avec toute autre moyenne de traitement se calculent de la manière suivante:
LSDa
=![]()
![]() (4.21)
(4.21)
LSD.05 = (2.16)(2.84) = 6.13
Dans toute expérience, une ou plusieurs variables de réponse peuvent être affectées par un certain nombre de facteurs dans le système global, dont certains sont maîtrisés ou maintenus aux niveaux voulus dans l’expérience. Une expérience dans laquelle les traitements sont constitués de toutes les combinaisons possibles de deux ou plusieurs facteurs, aux niveaux sélectionnés, est appelé plan d’expérience factoriel. Par exemple, une expérience sur l’enracinement des boutures englobant deux facteurs, mesurés à deux niveaux – par exemple deux hormones à deux dosages différents – est une expérience factorielle 2 x 2 ou 22. Les traitements sont constitués des quatre combinaisons possibles de chacun des deux facteurs, aux deux niveaux considérés.
|
Combinaison des traitements |
||
|
Numéro du traitement |
Hormone |
Dose (ppm) |
|
1 |
NAA |
10 |
|
2 |
NAA |
20 |
|
3 |
IBA |
10 |
|
4 |
IBA |
20 |
On utilise parfois l’expression expérience factorielle complète lorsque les traitements comprennent toutes les combinaisons des niveaux sélectionnés des facteurs, mais l’expression expérience factorielle fractionnée ne s’applique que le test ne porte que sur une fraction de toutes les combinaisons. Toutefois, pour simplifier, les expériences factorielles complètes seront, tout au long de ce manuel, appelées simplement expériences factorielles. On notera que le terme factoriel se réfère au mode de constitution spécifique des traitements et n’a rien à voir avec le plan décrivant le dispositif expérimental. Par exemple, si l’expérience factorielle 22 dont nous avons parlé plus haut fait partie d’un plan d’expérience en blocs aléatoires complets, l’expérience devrait être définie par l’expression expérience factorielle 22 dans un plan en blocs aléatoires complets.
Dans un plan d’expérience factoriel, le nombre total de traitements est égal au produit du nombre de niveaux de chaque facteur; dans l’exemple factoriel 22 , le nombre de traitements est égal à 2 x 2 = 4, dans une expérience factorielle 23, le nombre de traitements est 2 x 2 x 2 = 8.
Le nombre de traitements augmente rapidement avec le nombre de facteurs ou avec les niveaux de chaque facteur. Pour une expérience factorielle comprenant 5 clones, 4 espacements et 3 méthodes de désherbage, le nombre total de traitements sera 5 x 4 x 3 = 60. On évitera donc le recours inconsidéré aux expériences factorielles en raison de leur ampleur, de leur complexité et de leur coût. De plus, il est peu raisonnable de se lancer dans une expérience de grande ampleur au début d’un travail de recherche, alors qu’il est possible, avec plusieurs petits essais préliminaires, d’obtenir des résultats prometteurs. Imaginons par exemple qu’un généticien forestier ait fait venir 30 nouveaux clones d’un pays voisin et veuille voir comment ils réagissent à l’environnement local. Etant donné que normalement les conditions de l’environnement varient en fonction de plusieurs facteurs, tels que la fertilité du sol, le degré d’humidité, etc. l’idéal serait de tester les 30 clones dans le cadre d’une expérience factorielle englobant d’autres variables, telles que engrais, niveau d’humidité et densité de population. Le problème est que l’expérience devient alors extrêmement vaste du fait de l’adjonction d’autres facteurs que les clones. Même si l’on incluait qu’un seul facteur, comme l’azote ou l’engrais, à trois dosages différents, le nombre de traitements passerait de 30 à 90. Une expérience de cette ampleur pose divers types de problèmes, notamment pour obtenir des financements ou une surface expérimentale adéquate, ou pour contrôler l’hétérogénéité du sol etc. Pour faciliter les choses, il est donc préférable de commencer par tester les 30 clones dans une expérience à un facteur, puis de sélectionner sur la base des résultats obtenus un petit nombre de clones à soumettre à un examen plus détaillé. Par exemple la première expérience à un facteur peut montrer que seuls cinq clones ont des performances suffisamment remarquables pour justifier des tests plus approfondis. Ces cinq clones pourraient ensuite être insérés dans une expérience factorielle avec trois dosages d’azote, ce qui donnerait un expérience à quinze traitements , alors qu’il en faudrait 90 dans une expérience factorielle avec 30 clones.
L’effet d’un facteur est la variation moyenne d’une réponse dérivant d’un changement du niveau du facteur considéré. Cet effet est souvent appelé effet principal. Prenons pour exemple les données du Tableau 4.12.
Tableau 4.12. Données issues d’un plan d’expérience factorielle 2x2
|
Facteur B |
|||
|
Niveau |
b1 |
b2 |
|
|
a1 |
20 |
30 |
|
|
Facteur A |
|||
|
a2 |
40 |
52 |
|
L’effet principal du facteur A peut être considér é comme la différence entre la réponse moyenne au premier niveau de A et la réponse moyenne au deuxième niveau de A. Numériquement :
![]()
Ce résultat signifie que si le facteur A augmente du niveau 1 au niveau 2, la réponse augmente en moyenne de 21 unités. De même, l’effet principal du facteur B est
![]()
Si les facteurs apparaissent à plus de deux niveaux, la procédure ci-dessus doit être modifiée car les différences entre les réponses moyennes peuvent être exprimées de différentes manières.
Le principal avantage d’une expérience factorielle est qu’elle permet d’obtenir plus d’informations sur l’interaction entre les facteurs. Dans certaines expériences, on constate que la différence de réponse entre les niveaux d’un facteur n’est pas la même à tous les niveaux des autres facteurs, ce qui signifie qu’il existe une interaction entre les facteurs. Prenons pour exemple les données du Tableau 4.13.
Tableau 4.13. Données issues d’une expérience factorielle 2x2
|
Facteur B |
|||
|
Niveaux |
b1 |
b2 |
|
|
a1 |
20 |
40 |
|
|
Facteur A |
|||
|
a2 |
50 |
12 |
|
Au premier niveau du facteur B, l’effet du facteur A est
A = 50-20 = 30
Et au second niveau du facteur B, l’effet du facteur A est
A = 12-40 = -28
Etant donné que l’effet de A est fonction du niveau choisi pour le facteur B, il est évident qu’il existe une interaction entre A et B.
Ces concepts peuvent être illustrés par des graphiques. La figure 4.5 montre les données de réponse du Tableau 4.2, par rapport au facteur A pour les deux niveaux du facteur B.
Figure 4.5. Représentation graphique de l’absence d’interaction entre les facteurs.
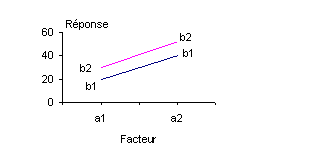
Les droites b1 et b2 sont presque parallèles, ce qui indique qu’il n’y a pas d’interaction entre les facteurs A et B.
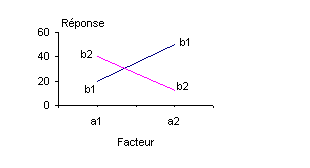
De même, la Figure 4.6 représente les données de réponse du Tableau 4.13. Dans ce cas, on constate que les droites b1 et b2 ne sont pas parallèles, ce qui indique une interaction entre les facteurs A et B. Si les graphiques de ce genre sont souvent très utiles pour interpréter des interactions significatives et signaler les résultats à des gestionnaires non qualifiés en statistique, ils ne doivent pas constituer la seule technique d’analyse des données, car leur interprétation est subjective et leur apparence souvent trompeuse.
Figure 4.6. Représentation graphique de l’interaction entre des facteurs.
On notera que lorsqu’une interaction est importante, les effets principaux correspondants ont peu de signification pratique. Pour les données du Tableau 4.13, l’effet principal estimé de A serait
![]() = 1
= 1
cette valeur étant très petite, nous sommes tentés de conclure à l’absence d’effets dus à A. Toutefois, si l’on examine les effets de A à différents niveaux du facteur B, on constate qu’il n’en est pas ainsi. Le facteur A a un effet, mais il dépend du niveau du facteur B, ce qui veut dire qu’une interaction significative masque souvent la signification des effets principaux. En présence d'une interaction significative, l'expérimentateur doit ordinairement examiner les niveaux d'un facteur, par exemple A, alors que le niveau des autres facteurs reste fixe, pour tirer des conclusions sur l’effet principal de A.
Dans la majorité des plans d’expérience factoriels, les traitements sont trop nombreux pour qu’un plan en blocs aléatoires puisse être efficace. Certains types de plans ont cependant été spécifiquement mis au point pour des expériences factorielles de grande envergure, (ex : plans factoriels avec confusion). L’utilisation de ces plans est décrite dans Das et Giri (1980).
4.4.1. Analyse de variance
Tout plan en blocs complets examiné dans les sections 4.2 et 4.3 pour des expériences à un facteur est applicable à un plan d’expérience factoriel. Les procédures de randomisation et de représentation schématique de chaque plan peuvent être appliquées directement, en ignorant simplement la composition factorielle des traitements et en faisant comme s’il n’existait pas de relation entre les traitements. Pour l’analyse de variance, les calculs examinés pour chaque plan sont aussi directement applicables. Toutefois, des étapes de calcul doivent être ajoutées pour répartir les sommes des carrés des traitements entre les composantes factorielles correspondant aux effets principaux des facteurs individuels et à leurs interactions. Cette procédure de fractionnement étant la même pour tous les plans en blocs complets, elle ne sera illustrée ici que pour le cas du PEBAC.
Nous allons décrire les différentes étapes de la procédure d’analyse de la variance d’une expérience à deux facteurs sur les bambous, avec deux niveaux d’espacements (Facteur A) et trois niveaux d’âge à la plantation (facteur B), définis dans un PEBAC, à trois répétitions. La liste des six combinaisons factorielles des traitements figure dans le Tableau 4.14, le dispositif expérimental est illustré à la Figure 4.7. et les données sont rassemblées dans le Tableau 4.15.
Tableau 4.14. Les combinaisons factorielles (2 x3) des traitements, avec deux niveaux d’espacement et trois niveaux d’âge.
|
Age à la plantation |
Espacement (en m) |
|
|
(en mois) |
10 m x 10 m |
12 m x 12m |
|
(a1) |
(a2) |
|
|
6 (b1) |
a1b1 |
a2b1 |
|
12 (b2) |
a1b2 |
a2b2 |
|
24 (b3) |
a1b3 |
a2b3 |
Figure 4.7. Schéma-type d’un plan d’expérience factoriel 2![]() 3 avec deux niveaux d’espacement et trois niveaux d’âge, dans un PEBAC, avec 3 répétitions.
3 avec deux niveaux d’espacement et trois niveaux d’âge, dans un PEBAC, avec 3 répétitions.
Répétition I Répétition II Répétition III
|
a2b3 |
a2b3 |
a1b2 |
||
|
a1b3 |
a1b2 |
a1b1 |
||
|
a1b2 |
a1b3 |
a2b2 |
||
|
a2b1 |
a2b1 |
a1b3 |
||
|
a1b1 |
a2b2 |
a2b1 |
||
|
a2b2 |
a1b1 |
a2b3 |
Tableau 4.15. Hauteur maximale moyenne de la tige de Bambusa arundinacea testée avec trois variantes d’âge et deux variantes d’espacement dans un PEBAC.
|
Combinaison des traitements |
Hauteur maximale de la tige d’une cépée (en cm) |
Total traitements |
||
|
|
Rép. I |
Rép. II |
Rép. III |
(Tij) |
|
a1b1 |
46.50 |
55.90 |
78.70 |
181.10 |
|
a1b2 |
49.50 |
59.50 |
78.70 |
187.70 |
|
a1b3 |
127.70 |
134.10 |
137.10 |
398.90 |
|
a2b1 |
49.30 |
53.20 |
65.30 |
167.80 |
|
a2b2 |
65.50 |
65.00 |
74.00 |
204.50 |
|
a2b3 |
67.90 |
112.70 |
129.00 |
309.60 |
|
Total répétitions (Rk) |
406.40 |
480.40 |
562.80 |
G=1449.60 |
*Etape 1. Soit r le nombre de répétitions, a le nombre de niveaux du facteur A (espacement), et b le nombre de niveaux du facteur B (âge). Dresser le tableau préliminaire de l’analyse de variance:
Tableau 4.16. Représentation schématique de l’analyse de variance d’une expérience factorielle avec deux niveaux du facteur A, trois niveauxs du facteur B et trois répétitions, dans un PEBAC
|
Source de variation |
Degrés de liberté (df) |
Somme des carrés (SS) |
Carré moyen
|
f calculé |
|
Répétition |
r-1 |
SSR |
MSR |
|
|
Traitement |
ab- 1 |
SST |
MST |
|
|
A |
a- 1 |
SSA |
MSA |
|
|
B |
b- 1 |
SSB |
MSB |
|
|
AB |
(a-1)(b-1) |
SSA B |
MSAB |
|
|
Erreur |
(r-1)(ab-1) |
SSE |
MSE |
|
|
Total |
rab -1 |
SSTO |
*Etape 2. Calculer les totaux des traitements (Tij), les totaux des répétitions (Rk), et le total général (G), comme indiqué dans le Tableau 4.15 et calculer SSTO, SSR, SST et SSE en suivant la procédure décrite dans la Section 4.3.3. Notons yijk l’observation correspondant au i-ème niveau du facteur A et au j-ème niveau du facteur B dans la k-ième répétition.
![]() (4.22)
(4.22)
![]()
SSTO 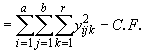 (4.23)
(4.23)
![]()
= 17479.10
SSR 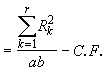 (4.24)
(4.24)
![]()
= 2040.37
SST 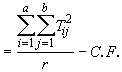 (4.25)
(4.25)
![]()
= 14251.87
SSE = SSTO - SSR - SST (4.26)
= 17479.10 - 2040.37 - 14251.87
= 1186.86
L’analyse de variance préliminaire figure dans le Tableau 4.17.
Tableau 4.17. Analyse de variance préliminaire des données du Tableau 4.15.
|
Source de variation |
Degré de liberté |
Somme des carrés |
Carré moyen |
F calculé |
F tabulaire 5% |
|
Répétition |
2 |
2040.37 |
1020.187 |
8.59567* |
4.10 |
|
Traitement |
5 |
14251.87 |
2850.373 |
24.01609* |
3.33 |
|
Erreur |
10 |
1186.86 |
118.686 |
||
|
Total |
17 |
17479.10 |
*Significatif au seuil de 5% .
*Etape 3. Construire le tableau à double entrée des totaux facteur A x facteur B, avec le calcul des totaux du facteur A et les totaux du facteur B. Dans notre exemple, le tableau des totaux Espacement x Age (AB), avec les totaux de l’espacement (A) et les totaux de l’âge (B) calculés, est illustré au Tableau 4.18
Tableau 4.18. Tableau des totaux Espacement x Age , pour les données du Tableau 4.15.
|
Age |
Espacement |
Total |
|
|
a1 |
a2 |
(Bj) |
|
|
b1 |
181.10 |
167.80 |
348.90 |
|
b2 |
187.70 |
204.50 |
392.20 |
|
b3 |
398.90 |
309.60 |
708.50 |
|
Total (Ai) |
767.70 |
681.90 |
G = 1449.60 |
*Etape 4. Calculer les trois composantes factorielles de la somme des carrés des traitements:
SSA =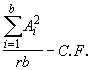 (4.27)
(4.27)
![]()
= 408.98
SSB = 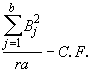 (4.28)
(4.28)
![]()
= 12846.26
SSAB = SST - SSA - SSB (4.29)
= 14251.87 - 408.98 - 12846.26
= 996.62
*Etape 5. Calculer le carré moyen de chaque source de variation en divisant chaque somme des carrés par les degrés de liberté qui lui sont associés et obtenir les valeur du rapport F pour les trois composantes factorielles, selon le schéma du Tableau 4.16.
*Etape 6. Entrer toutes les valeurs obtenues durant les Etapes 3 à 5, dans l’analyse de variance préliminaire de l’Etape 2 en suivant les indications du Tableau 4.19.
Tableau 4.19. Analyse de variance des données du Tableau 4.15 issues d’une expérience factorielle 2 x 3 dans un PEBAC.
|
Source de variation |
Degré de liberté |
Somme des carrés |
Carré moyen |
F calculé |
F tabulaire 5% |
|
Répétition |
2 |
2040.37 |
1020.187 |
8.60* |
4.10 |
|
Traitement |
5 |
14251.87 |
2850.373 |
24.07* |
3.33 |
|
A |
1 |
12846.26 |
6423.132 |
3.45 |
4.96 |
|
B |
2 |
408.98 |
408.980 |
54.12* |
4.10 |
|
AB |
2 |
996.62 |
498.312 |
4.20* |
4.10 |
|
Erreur |
10 |
1186.86 |
118.686 |
||
|
Total |
17 |
17479.10 |
*Significatif au seuil de 5%
*Etape 7. Comparer chaque valeur calculée de F avec la valeur tabulaire de F figurant l’Annexe 3, avec f1 = df du MS du numérateur et f2 = df du MS du dénominateur, au seuil de signification voulu. Par exemple, la valeur calculée de F relative à l’effet principal du facteur A est comparée avec les valeurs tabulaires de F (avec f1=1 et f2=10 degrés de liberté) de 4.96, au seuil de signification de 5%. Le résultat indique que l’effet principal du facteur A (espacement) n’est pas significatif au seuil de 5%.
*Etape 8. Calculer le coefficient de variation:
![]() (4.30)
(4.30)
![]()
4.4.2. Comparaison de moyennes
Dans une expérience factorielle, on effectue différents types de comparaisons d’effets. Par exemple, dans une expérience factorielle 2 x 3, quatre types de moyennes peuvent être comparées :
Type-(1) Les deux moyennes de A, calculées sur la base des trois niveaux du facteur B
Type-(2) Les trois moyennes de B calculées sur la base des deux niveaux du facteur A
Type (3) Les six moyennes de A, deux moyennes à chacun des trois niveaux du facteur B
Type (4) Les six moyennes de B, trois moyennes à chacun des deux niveaux du facteur A
La moyenne de Type-(1) est une moyenne de 3r observations, celle de Type-(2) est une moyenne de 2r observations et celles de Type-(3) ou de Type-(4) sont des moyennes de r observations. Ainsi, la formule ![]() n’est appropriée que pour la différence moyenne mettant en jeu des moyennes de Type-(3) ou de Type-(4). Dans les moyennes de Type-(1) et de Type-(2), le diviseur r de la formule doit être remplacé respectivement par 3r et 2r. Autrement dit, pour comparer deux moyennes de A, calculées sur la base de tous les niveaux du facteur B, la valeur
n’est appropriée que pour la différence moyenne mettant en jeu des moyennes de Type-(3) ou de Type-(4). Dans les moyennes de Type-(1) et de Type-(2), le diviseur r de la formule doit être remplacé respectivement par 3r et 2r. Autrement dit, pour comparer deux moyennes de A, calculées sur la base de tous les niveaux du facteur B, la valeur ![]() se calcule selon la relation
se calcule selon la relation ![]() et pour comparer toute paire de moyennes de B, calculée sur la base de tous les niveaux du facteur A, la formule de calcul de la valeur
et pour comparer toute paire de moyennes de B, calculée sur la base de tous les niveaux du facteur A, la formule de calcul de la valeur ![]() est
est ![]() ou plus simplement
ou plus simplement ![]() .
.
A titre d’exemple, prenons l’expérience factorielle 2 x 3 dont les données sont reportées dans le Tableau 4.15. L’analyse de variance met en lumière une interaction significative entre l’espacement et l’âge, l’effet de l’âge variant si l’espacement change. Il est donc inutile de comparer les moyennes d’âge, par rapport à tous les niveaux d’espacement ou les moyennes des espacements par rapport à tous les niveaux d’âge. Il est plus approprié d’effectuer des comparaisons entre les moyennes d’âge, pour un même niveau d’espacement, ou entre les moyennes d’espacement, pour un même niveau d’âge. La comparaison entre les moyennes d’espacement, au même âge, est illustrée dans le passage qui suit. Les étapes du calcul de la PPDS pour la comparaison de deux moyennes d’espacement au même âge sont les suivantes :
*Etape 1.Calculer l’erreur-type de la différence moyenne d’après la formule applicable pour une comparaison de Type-(3)
![]() (4.31)
(4.31)
= ![]()
où la valeur du MS de l’erreur ( 118.686) est extraite de l’analyse de variance du Tableau 4.19.
*Etape 2. Tirer de l’Annexe 2 la valeur tabulaire de t value pour df de l’erreur (10 df), soit 2.23 au seuil de signification de 5% et calculer la PPDS, à l’aide de l’expression,
![]() =
=![]()
*Etape 3. Dresser le tableau à deux entrées des moyennes du produit de l’espacement x Age, comme indiqué dans le Tableau 4.20. Pour chaque paire de niveaux d’espacement à comparer au même niveau d’âge, calculer la différence moyenne et la comparer avec la valeur de la PPDS obtenue durant l’Etape 2. Par exemple, la différence moyenne de hauteur de la tige entre deux niveaux d’espacement, à l’âge de 12 mois à la plantation, est égale à 5,6 cm. Etant donné que cette valeur est inférieure à la valeur de la PPDS au seuil de signification de 5%, la différence n’est pas significative.
Tableau 4.20. Tableau des moyennes Espacement x Age de la hauteur des tiges, sur la base des données du Tableau 4.15
|
Age à la plantation |
Espacement (en m) |
|
|
(en mois) |
10 m x 10 m |
12 m x 12m |
|
Hauteur moyenne de la tige (en cm) |
||
|
6 |
60.37 |
55.93 |
|
12 |
62.57 |
68.17 |
|
24 |
132.97 |
103.20 |
Dans un plan d’expérience factoriel, si le nombre de facteurs à tester est trop grand, il devient impossible de tester tous les traitements factoriels à la fois dans le cadre d’une seule expérience. Il est alors plus logique de mettre au point un plan expérimental pour tester une fraction seulement du nombre total de traiteme nts. Le plan factoriel fractionné (PFF) est applicable, uniquement dans le cas d’expériences englobant un grand nombre de facteurs. Il permet de sélectionner et de tester systématiquement une fraction seulement de l’ensemble complet de combinaisons de traitements factoriels. Ceci entraîne malheureusement une perte d’informations sur certains effets sélectionnés au préalable. Alors que ces pertes peuvent être importantes dans des expériences à un ou deux facteurs, elles sont plus tolérables si les facteurs sont nombreux. Le nombre d’effets d’interaction augmente rapidement avec le nombre de facteurs, ce qui permet une certaine flexibilité dans le choix des effets qui devront être sacrifiés. De fait, lorsque l’on sait avant de commencer que certains effets spécifiques sont faibles ou sans importance, la perte d’information dérivant de l’adoption d’un Plan d’expérience factoriel fractionné est négligeable.
Dans la pratique, les effets qui sont le plus couramment sacrifiés du fait du recours au PFF sont des interactions d’ordre élevé – de quatre facteurs ou de cinq facteurs, voire interaction de trois facteurs. Dans la majorité des cas, à moins de disposer d’informations préalables en sens contraire, le chercheur a intérêt à sélectionner un ensemble de traitements qui permet de tester tous les effets principaux et les interactions de deux facteurs. En recherche forestière, le PFF sera utilisé dans des essais exploratoires ayant pour principal objectif d’examiner les interactions entre des facteurs. Pour ces essais, les PFF les plus appropriés sont ceux qui ne sacrifient que les interactions concernant plus de deux facteurs.
Avec le PFF, le nombre d’effets mesurables décroît rapidement avec la diminution du nombre de traitements à tester. Ainsi, lorsque les effets à mesurer sont nombreux, le nombre de traitements à tester, même dans le cadre d’un PFF, peut être encore trop important. Il est alors possible de diminuer encore la taille de l’expérience en réduisant le nombre de répétitions. Bien que les PFF sans répétition soient rarement employés dans les expériences forestières, lorsqu’on les applique à des essais exploratoires, le nombre de répétitions requis peut être réduit au minimum.
L’autre avantage du PFF est qu’il permet de réduire la taille des blocs puisque ceux-ci ne doivent plus nécessairement contenir tous les traitements à soumettre au test. L’homogénéité des unités expérimentales appartenant à un même bloc peut ainsi être améliorée. La réduction de la taille des blocs s’accompagne toutefois d’une perte d’information qui s’ajoute à celle dérivant de la diminution du nombre de traitements. Ainsi, le PFF peut être conçu sur mesure et adapté à la majorité des plans d’expérience factoriels. Cependant, la procédure à employer à cette fin est complexe, c’est pourquoi nous nous limiterons ici à décrire une catégorie particulière de PFF, adaptée au cas d’essais exploratoires dans le domaine de la recherche forestière. Les principales caractéristiques de ces plans d’expérience spécifiques sont les suivantes : i) ils s’appliquent uniquement aux expériences factorielles 2’’ où n, le nombre de facteurs est de 5 au minimum, ii) ils comprennent seulement la moitié de l’ensemble complet de combinaisons de traitements factoriels, dénoté par 2n-1 ; iii) ils permettent d’estimer la totalité des effets principaux et des interactions à deux facteurs. Pour des plans plus complexes, le lecteur peut se référer à Das et Giri (1980).
La procédure de définition du schéma et d’analyse de variance d’un PFF 25-1 , avec un essai en champ comportant cinq facteurs A, B, C, D et E est illustrée dans la section suivante. Les différentes combinaisons des traitements sont désignés par les lettres a, b, c,…, pour noter la présence (ou le niveau élevé) des facteurs A, B, C,… Ainsi, la combinaison du traitement ab, dans une expérience factorielle 25 indique une combinaison de traitement caractérisée par un niveau élevé (ou par la présence) des facteurs A et B et par un bas niveau (ou par l’absence) des facteurs C, D et E. En revanche, dans une expérience factorielle 26, cette même notation (ab) se référerait à une combinaison de traitement contenant un niveau élevé des facteurs A et B et un bas niveau des facteurs C, D, E, et F. Dans tous les cas, le symbole (1) indiquera la combinaison de traitement caractérisée par un bas niveau de tous les facteurs.
4.5.1. Elaboration du plan et présentation
Il existe une méthode simple pour trouver la fraction voulue des combinaisons factorielles dans un PFF 25-1 , sachant que, dans un essai factoriel 25, l’effet des facteurs ABCDE peut être estimé à partir du développement du terme (a-1)(b-1)(c-1)(d-1)(e-1):
(a-1)(b-1)(c-1)(d-1)(e-1) = abcde - acde - bcde + cde - abde + ade + bde - de
- abce + ace + bce - ce + abe - ae - be + e
- abcd + acd + bcd - cd + abd - ad - bd + d
+ abc - ac - bc + c - ab + a + b - 1
Dans cette expression, les signes (positif ou négatif) associés aux traitements permettent de diviser l’ensemble factoriel complet en deux groupes de traitements. Si l’on conserve uniquement un l’un des deux ensembles, positif ou négatif, on obtient une demie fraction de l’expérience factorielle 25. Les deux séries de traitements se présentent comme suit.
|
Traitements accompagnés de signes négatifs |
Traitements accompagnés de signes positifs |
|
acde, bcde, abde, de, abce, ce, ae, be, |
abcde, bcde, abde, de, abce, ce, ae, be, |
|
abcd, cd, ad, bd, ac, bc, ab, 1 |
abcd, cd, ad, bd, ac, bc, ab, 1 |
Par suite de la réduction du nombre de traitements inclus dans l’expérience, il va être impossible d’ estimer l’effet ABCDE à partir de l’ensemble fractionné. Tous les effets principaux et toutes les interactions de deux facteurs peuvent être estimés dans l’hypothèse où toutes les interactions de trois facteurs et d’ordre plus élevé sont négligeables. La procédure peut être généralisée puisque dans une expérience 26, , il est possible d’isoler une demie fraction en retenant les traitements accompagnés d’un signe positif ou négatif dans le développement de (a-1)(b-1)(c-1)(d-1)(e-1)(f-1).
Le PFF est simplement un dispositif qui permet de sélectionner des traitements ayant une structure factorielle, et les combinaisons des facteurs qui en découlent peuvent être considérées comme un ensemble de traitements applicables à l’expérience physique qui sera définie dans un plan standard quelconque tel que PER ou PEBAC. On trouvera à la Figure 4.8. un schéma randomisé type, pour un PFF 25-1 avec deux répétitions faisant partie d’un PEBAC.
Figure 4.8. Schéma-type d’un PFF 25-1 avec deux répétitions faisant partie d’un PEBAC.
|
1 de |
9 ab |
1 abce |
9 acde |
|
|
2 1 |
10 adde |
2 cd |
10 bd |
|
|
3 acde |
11 ad |
3 be |
11 de |
|
|
4 ae |
12 abce |
4 ad |
12 bcde |
|
|
5 ce |
13 be |
5 ae |
13 ce |
|
|
6 ac |
14 bc |
6 abcd |
14 1 |
|
|
7 bcde |
15 bcd |
7 abce |
15 ac |
|
|
8 bd |
16 cd |
8 bc |
16 be |
Répétition I Répétition II
4.5.2. Analyse de variance
La procédure d’analyse de variance applicable à un PFF 25-1 à deux répétitions, est illustrée à l’aide de la méthode de Yates pour le calcul de la somme des carrés, qui facilite le calcul manuel d’expériences factorielles de grande ampleur. On peut aussi appliquer les règles standards de calcul des sommes des carrés dans l’analyse de variance, en élaborant des tableaux à une entrée des totaux, pour calculer les effets principaux, des tableaux à double entrée des totaux pour les interactions de deux facteurs, etc, en suivant la méthode illustrée dans la Section 4.4.1.
L’analyse d’un PFF 25-1 est illustrée avec des données hypothétiques issue d’un essai dont le schéma, décrit à la Figure 4.8, est conforme à celui d’un PEBAC. La réponse aux différentes combinaisons de traitement, mesurée par le rendement en fourrage (tonnes/ha), est reportée dans le Tableau 4.21. Les cinq facteurs étaient liés aux différentes composantes d’un programme d’aménagement du sol (application de matière organique, fertilisation, désherbage, irrigation et chaulage).
Tableau 4.21. Données sur le rendement en fourrage dérivées d’une expérience factorielle 25-1
|
Combinaison de traitement |
Rendement en fourrage (t/ha) |
Total du traitement (Ti) |
|
|
Replication I |
Replication II |
||
|
acde |
1.01 |
1.04 |
2.06 |
|
bcde |
1.01 |
0.96 |
1.98 |
|
abde |
0.97 |
0.94 |
1.92 |
|
de |
0.82 |
0.75 |
1.58 |
|
abce |
0.92 |
0.95 |
1.88 |
|
ce |
0.77 |
0.75 |
1.53 |
|
ae |
0.77 |
0.77 |
1.55 |
|
be |
0.76 |
0.80 |
1.57 |
|
abcd |
0.97 |
0.99 |
1.97 |
|
cd |
0.92 |
0.88 |
1.80 |
|
ad |
0.80 |
0.87 |
1.68 |
|
bd |
0.82 |
0.80 |
1.63 |
|
ac |
0.91 |
0.87 |
1.79 |
|
bc |
0.79 |
0.76 |
1.55 |
|
ab |
0.86 |
0.87 |
1.74 |
|
1 |
0.73 |
0.69 |
1.42 |
|
Total répétition (Rj) |
13.83 |
13.69 |
|
|
Total général (G) |
27.52 |
||
L’analyse de variance se calcule en plusieurs étapes :
*Etape 1. Dresser le tableau préliminaire de l’analyse de variance présentée dans le Tableau 4.22.
*Etape 2. Déterminer le nombre de facteurs réels (k) avec deux niveaux chacun, donnant lieu à un nombre total de traitements factoriels égal au nombre de traitements (t) inclus dans l’expérience (2k = t). Sélectionner ensuite l’ensemble des k facteurs réels particuliers dans l’ensemble initial de n facteurs. Les (n - k) facteurs restants sont appelés facteurs factices. Dans notre exemple, les t = 16 combinaisons de traitements correspondent à un ensemble complet de 2k combinaisons factorielles avec k = 4. Dans un souci de simplification, nous dirons que les quatre premiers facteurs A, B, C et D sont les facteurs réels, E étant le facteur factice.