


Tableau 4.22. Représentation schématique de l’analyse de variance d’un PFF 25-1 à deux répétitions, s’inscrivant dans un PEBAC.
|
Source de variation |
Degré de liberté (df) |
Somme des carrés (SS) |
Carré moyen |
F calculé |
|
Bloc |
r-1=1 |
SSR |
MSR |
|
|
A |
1 |
SSA |
MSA |
|
|
B |
1 |
SSB |
MSB |
|
|
C |
1 |
SSC |
MSC |
|
|
D |
1 |
SSD |
MSD |
|
|
E |
1 |
SSE@ |
MSE@ |
|
|
AB |
1 |
SSAB |
MSAB |
|
|
AC |
1 |
SSAC |
MSAC |
|
|
AD |
1 |
SSAD |
MSAD |
|
|
AE |
1 |
SSAE |
MSAE |
|
|
BC |
1 |
SSBC |
MSBC |
|
|
BD |
1 |
SSBD |
MSBD |
|
|
BE |
1 |
SSBE |
MSBE |
|
|
CD |
1 |
SSCD |
MSCD |
|
|
CE |
1 |
SSCE |
MSCE |
|
|
DE |
1 |
SSDE |
MSDE |
|
|
Erreur |
15 |
SSE |
MSE |
|
|
Total |
(r 25-1)-1 |
SSTO |
@
Cette SS est la somme des carrés dus au facteur E, à ne pas confondre avec la somme des carrés dus à l’erreur (SSE) figurant plus bas dans le tableau. Le degré de liberté de l’erreur peut être obtenu en soustrayant du degré de liberté total le degré de liberté relatif au bloc et les effets factoriels.*Etape 3. Ranger les t traitements dans un ordre logique, d’après les k facteurs réels, en commençant par les traitements ayant le plus petit nombre de lettres (ab avant abc, abc avant abcd, et ainsi de suite). Si le traitement (1) est présent dans l’ensemble de t traitements, il est toujours le premier de la liste. Les traitements ayant le même nombre de lettres son rangés suivant l’ordre lexicographique. Par exemple, ab est devant ac, ad devant bc, et ainsi de suite. Toutes les lettres d’identification des traitements correspondant à des facteurs factices sont ignorées dans le processus de classement. Dans notre exemple, le facteur E est le facteur factice ; la combinaison ae est donc simplement notée a, de sorte qu’elle vient avant ab. Les 16 traitements de notre exemple, classés dans cet ordre logique, figurent dans la première colonne du Tableau 4.23. On notera que les traitements sont énumérés systématiquement, sans tenir compte de leur allocation dans les blocs, et que le facteur factice E est indiqué entre parenthèses.
*Etape 4. Calculer les t totaux des effets factoriels: Prendre les totaux des traitements t comme ensemble initial ou valeurs de T0. Dans notre exemple, l’ensemble des 16 valeurs de T0, rangées dans l’ordre logique, est reporté dans la deuxième colonne du Tableau 4.23. Ensuite, regrouper les valeurs de T0 en deux paires successives t/2. Dans notre exemple, les paires successives sont au nombre de 8 : la première paire est 1.42 et 1.54, la seconde est 1.56 et 1.73, et la dernière est 1.97 et 1.96. Ajouter les valeurs des deux traitements dans chacune des paires t/2 formées. Les résultats constituent la première moitié du deuxième ensemble, ou valeurs de T1. Dans notre exemple, la première moitié des valeurs de T1 se calcule comme suit :
= 1.42 + 1.54
3.29 = 1.56 + 1.73
….
….
3.93 = 1.97 + 1.96
Dans chacune des t/2 paires de T0, soustraire la première valeur de la seconde pour former la moitié basse des valeurs de T1 . Dans notre exemple, la deuxième moitié des valeurs de T1 se calcule comme suit :
-0.12 = 1.42 - 1.54
-0.17 = 1.56 - 1.73
….
….
0.01 = 1.97 - 1.96
Les résultats de ces opérations sont reportés dans la troisième colonne du Tableau 4.23.
Refaire les opérations précédentes, en utilisant à présent les valeurs de T1 à la place des valeurs de T0 pour dériver le troisième ensemble, ou valeurs de T2. Dans notre exemple, les résultats des opérations appliquées aux valeurs de T1 pour obtenir les valeurs de T2 figurent dans la quatrième colonne du Tableau 4.23. Répétez l’opération (n - 1) fois, où n est le nombre total de facteurs compris dans l’expérience. A chaque fois, utilisez les nouvelles valeurs dérivées de T. Dans notre exemple, l’opération est répétée encore deux fois pour dériver les valeurs de T3 et de T4, reportées dans la cinquième et la sixième colonnes du Tableau 4.23.
Tableau 4.23. Application de la méthode de Yates, pour le calcul des sommes des carrés d’un PFF 25-1 avec les données du Tableau 4.21
|
Traitement |
T0 |
T1 |
T2 |
T3 |
T4 |
Identification de l’effet factoriel |
|
|
|
|
Initial |
Final |
||||||
|
(1) |
1.42 |
2.96 |
6.25 |
12.97 |
27.52 |
(G) |
(G) |
23.667 |
|
a(e) |
1.54 |
3.29 |
6.72 |
14.55 |
-1.50 |
A |
AE |
0.070 |
|
b(e) |
1.56 |
3.30 |
6.77 |
-0.87 |
-0.82 |
B |
BE |
0.021 |
|
ab |
1.73 |
3.42 |
7.78 |
-0.63 |
0.04 |
AB |
AB |
0.000 |
|
c(e) |
1.52 |
3.24 |
-0.29 |
-0.45 |
-1.48 |
C |
CE |
0.068 |
|
ac |
1.78 |
3.53 |
-0.58 |
-0.37 |
0.14 |
AC |
AC |
0.001 |
|
bc |
1.55 |
3.85 |
-0.39 |
0.11 |
-0.42 |
BC |
BC |
0.006 |
|
abc(e) |
1.87 |
3.93 |
-0.24 |
-0.07 |
0.44 |
ABC |
D |
0.006 |
|
d(e) |
1.57 |
-0.12 |
-0.33 |
-0.47 |
-1.58 |
D |
DE |
0.078 |
|
ad |
1.67 |
-0.17 |
-0.12 |
-1.01 |
-0.24 |
AD |
AD |
0.002 |
|
bd |
1.62 |
-0.26 |
-0.29 |
0.29 |
-0.08 |
BD |
BD |
0.000 |
|
abd(e) |
1.91 |
-0.32 |
-0.08 |
-0.15 |
0.18 |
ABD |
C |
0.001 |
|
cd |
1.80 |
-0.10 |
0.05 |
-0.21 |
0.54 |
CD |
CD |
0.009 |
|
acd(e) |
2.05 |
-0.29 |
0.06 |
-0.21 |
0.44 |
ACD |
B |
0.006 |
|
bcd(e) |
1.97 |
-0.25 |
0.19 |
-0.01 |
0.00 |
BCD |
A |
0.000 |
|
abcd |
1.96 |
0.01 |
-0.26 |
0.45 |
-0.46 |
ABCD |
E |
0.007 |
*Etape 5. Identifier l’effet factoriel spécifique représenté par chacune des valeurs du dernier ensemble (communément appelé totaux des effets factoriels) dérivées lors de l’Etape 4. Procéder somme suit : la première valeur représente le total général (G). En ce qui concerne les (t – 1)valeurs restantes, assignez les effets factoriels préliminaires conformément aux lettres des traitements correspondants, en ignorant les facteurs factices.
Par exemple, la seconde valeur de T4 correspond aux combinaisons de traitement a (e), de sorte qu’elle est assignée à l’effet principal A. La quatrième valeur de T4 correspond au traitement ab et est assignée à l’effet de l’interaction AB, et ainsi de suite. Les résultats relatifs aux 16 traitements sont reportés dans la septième colonne du Tableau 4.23. Pour les traitements dans lesquels intervient le facteur factice, ajuster les effets factoriels préliminaires comme suit. Identifier tous les effets associés au facteur factice E pouvant être estimés dans le cadre du plan. Dans notre exemple, ceux-ci sont l’effet principal de E et la totalité de ses interactions à deux facteurs AE, BE, CE et DE. Identifier les alias de tous les effets énumérés comme "préliminaires ". L’alias de tout effet est défini comme étant l’interaction généralisée de cet effet avec le contraste déterminant. L’interaction généralisée entre deux effets factoriels quelconques s’obtient en combinant toutes les lettres qui apparaissent dans les deux effets puis en supprimant toutes celles que l’on retrouve deux fois. Par exemple, l’interaction généralisée entre ABC et AB est AABBC ou C. Dans notre exemple, le contraste déterminant est ABCDE, les alias des cinq effets associés au facteurs factice E sont : E=ABCD, AE=BCD, BE=ACD, CE=ABD et DE=ABC.
Les deux effets factoriels intervenant dans chaque paire d’alias (l’un à gauche, et l’autre à droite du signe égal) sont indissociables (ils ne peuvent pas être estimés séparément). Par exemple, pour la première paire (E et ABCD), l’effet principal du facteur E, ne peut pas être séparé de l’effet d’interaction ABCD. A moins que l’on sache qu’une des paires est absente, il n’y a donc aucun moyen de savoir quelle est celle qui contribue à l’estimation obtenue.
Remplacer tous les effets factoriels préliminaires qui sont des alias des effets estimables associés au facteur factice, par ce dernier facteur. Par exemple, étant donné que ABCD (dernier traitement du Tableau 4.23) est l’alias de E, il est remplacé par E. De la même manière, BCDE est remplacé par A, ACDE par B et ainsi de suite… Les résultats finaux de l’identification des effets factoriels figurent dans la huitième colonne du Tableau 4.23.
*Etape 6. Ajouter au Tableau 4.23 une colonne supplémentaire![]() , où r est le nombre de répétitions et n le nombre de facteurs inclus dans l’expérience. La valeur de cette colonne correspondant à G dans la colonne précédente sera le facteur de correction. Les autres valeurs de cette colonne seront la somme des carrés correspondant aux effets identifiés dans la colonne précédente.
, où r est le nombre de répétitions et n le nombre de facteurs inclus dans l’expérience. La valeur de cette colonne correspondant à G dans la colonne précédente sera le facteur de correction. Les autres valeurs de cette colonne seront la somme des carrés correspondant aux effets identifiés dans la colonne précédente.
*Etape 7. Calculer les SS dûs aux autres effets pour compléter l’analyse de la variance. Supposons que yij représente la valeur obtenue avec le i- ème traitement de la j-ème répétition.
![]() (4.32)
(4.32)
= ![]() = 23.6672
= 23.6672
SSTO 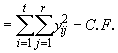 (4.33)
(4.33)
![]()
= 0.2866
SSR 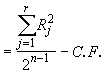 (4.34)
(4.34)
![]()
= 0.0006
SST 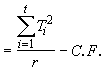 (4.35)
(4.35)
![]()
= 0.2748
SSE = SSTO - SSR - SST (4.36)
= 0.2866 - 0.2748 - 0.0006
= 0.01
*Etape 8. Calculer le carré moyen (MS) de chaque source de variation en divisant chaque SS par son degré de liberté df. Ici, le MS correspondant à chaque effet factoriel sera égal à sa SS puisque, dans chaque cas, le df de ces effets est égal à 1.
*Etape 9. Calculer la valeur de F correspondant à chaque terme du tableau d’analyse de variance en divisant les valeurs de MS par les valeurs des MS de l’erreur. L’analyse de variance finale est illustrée au Tableau 4.24.
Tableau 4.24. Analyse de variance des données du Tableau 4.21 correspondant à un plan d’expérience factoriel 25-1.
|
Source de variation |
Degrés de liberté |
Sommes des carrés |
Carrés moyens |
F calculé |
F Tabulaire5% |
|
Répétition |
1 |
0.0006 |
0.0006 |
0.86ns |
4.54 |
|
A |
1 |
0.000 |
0.000 |
0.00 ns |
4.54 |
|
B |
1 |
0.006 |
0.006 |
8.57* |
4.54 |
|
C |
1 |
0.001 |
0.001 |
1.43 ns |
4.54 |
|
D |
1 |
0.006 |
0.006 |
8.57* |
4.54 |
|
E |
1 |
0.007 |
0.007 |
10.00* |
4.54 |
|
AB |
1 |
0.000 |
0.000 |
0.00 ns |
4.54 |
|
AC |
1 |
0.001 |
0.001 |
1.43 ns |
4.54 |
|
AD |
1 |
0.002 |
0.002 |
2.86 ns |
4.54 |
|
AE |
1 |
0.070 |
0.070 |
100.00* |
4.54 |
|
BC |
1 |
0.006 |
0.006 |
8.57* |
4.54 |
|
BD |
1 |
0.000 |
0.000 |
0.00 ns |
4.54 |
|
BE |
1 |
0.021 |
0.021 |
30.00* |
4.54 |
|
CD |
1 |
0.009 |
0.009 |
12.86* |
4.54 |
|
CE |
1 |
0.068 |
0.068 |
97.14* |
4.54 |
|
DE |
1 |
0.078 |
0.078 |
111.43* |
4.54 |
|
Erreur |
15 |
0.010 |
0.0007 |
||
|
Total |
31 |
0.2866 |
* Significatif au seuil de 5% l, ns = non significatif au seuil de 5%
*Etape 11.Comparer chaque valeur calculée de F avec les valeurs tabulaires de F correspondantes, tirées de l’Annexe 3, avec f1 = df du MS du numérateur et f2 = df de l’erreur. Les résultats montrent que les effets principaux B, D et E et les interactions de deux facteurs AE, BC, BE, CD, CE et AE sont hautement significatifs et que les effets principaux A et C et les interactions de deux facteurs AB, AC, AD et BD ne sont pas significatives.
4.5.3. Comparaison de moyennes
La procédure décrite dans la section 4.4.2. pour comparer des moyennes dans des plans d’expérience factoriels complets s’applique également dans le cas d’un PFF. Il ne faut pas oublier toutefois que, dans un plan d’expérience factoriel 25-1, seules les moyennes de t ableaux à une ou deux entrées peuvent être comparées à l’aide de la procédure des comparaisons multiples.
4.6. Dispositif en parcelles divisées
L’expérience avec parcelles divisées (ou dispositif en tiroir) convient très bien dans le cas d’une expérience à deux facteurs dans laquelle les niveaux d’un des deux facteurs ne peuvent être testés que dans des parcelles de grande taille et se caractérisent par des effets très différents. Dans une telle situation, l’expérience sera formée d’un ensemble de " grandes parcelles " dans lesquelles des niveaux sont assignés au facteur de grande parcelle. Chaque grande parcelle est divisée en petites parcelles auxquelles est assigné le second facteur. Chaque grande parcelle devient ainsi un bloc pour les traitements des petites parcelles (c’est-à-dire les niveaux du facteur de petite parcelle). Le facteur de grande parcelle peut en réalité être alloué suivant l’un des systèmes existant ( plan entièrement randomisé, plan en blocs aléatoires complets, ou carré latin) mais ici seul le plan entièrement randomisé est envisagé pour le facteur de grande parcelle, car c’est probablement le plan le plus approprié et le plus couramment employé pour les expériences forestières.
Avec un dispositif en parcelles divisées, la précision de la mesure des effets du facteur de grande parcelle est sacrifiée au profit de celle du facteur de la petite parcelle. La mesure de l’effet principal du facteur de petite parcelle et son interaction avec le facteur de grande parcelle sont plus précises que celles qui peuvent être obtenues avec un plan en blocs aléatoires complets. En revanche, la mesure des effets des traitements des grandes parcelles (les niveaux du facteur des grandes parcelles) est moins précise que celle que l’on obtiendrait avec un plan en blocs aléatoires complets.
4.6.1. Dispositif
Un dispositif en parcelles divisées comprend deux processus de randomisation distincts – un pour les grandes parcelles et l’autre pour les petites parcelles. Dans chaque répétition, on commence par allouer au hasard les traitements des grandes parcelles, puis ceux des petites parcelles formées à l’intérieur de chaque grande parcelle.
Ceci sera illustré par une expérience à deux facteurs comprenant quatre niveaux d’azote (traitements des grandes parcelles) et trois clones d’eucalyptus (traitement des petites parcelles), avec trois répétitions. Ici, les doses d’engrais ont été choisies pour les grandes parcelles, principalement en fonction de leur facilité d’application et de contrôle de l’effet de lessivage et pour détecter la présence d’une interaction entre les engrais et les clones. Dans notre description des étapes de la randomisation et de la définition d’un dispositif en parcelles divisées, a est le nombre de traitements des grandes parcelles, b est le nombre de traitements des petites parcelles et r est le nombre de répétitions.
*Etape 1. Diviser la surface expérimentale en r = 3 blocs, dont chacun sera divisé en a = 4 grandes parcelles, comme dans la Figure 4.9.
*Etape 2. Suivant la procédure de randomisation d’un PEBAC avec a = 4 traitements et r = 3 répétitions allouer au hasard les 4 traitements à l’azote aux 4 grandes parcelles se trouvant à l’intérieur des 3 blocs. Le résultat se présentera comme dans la Figure 4.10.
*Etape 3. Diviser chacune des ra = 12 grandes parcelles en b = 3 petites parcelles et en suivant la procédure de randomisation d’un PEBAC pour b = 3 traitements et ra = 12 répétitions, allouer au hasard les 3 clones aux 3 petites parcelles se trouvant dans chacune des 12 grandes parcelles. Le résultat se présentera comme dans la Figure 4.11.
Figure 4.9. Division de la surface expérimentale en trois blocs (répétitions) composés de quatre grandes parcelles, comme première étape de la définition d’une expérience en parcelles divisées comportant trois répétitions et quatre traitements par grande parcelle.
|
Grandes parcelles |
Grandes parcelles |
Grandes parcelles |
|||||||||||
|
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
||
|
Répétition I |
Répétition II |
Répétition III |
|||||||||||
Figure 4.10. Allocation aléatoire de quatre niveaux d’azote (n0, n1, n2 et n3) aux quatre grandes parcelles, dans chacune des trois répétitions de la Figure 4.9.
|
n3 |
n1 |
n0 |
n2 |
n1 |
n0 |
n3 |
n2 |
n0 |
n1 |
n2 |
n3 |
||
|
Répétition I |
Répétition II |
Répétition III |
|||||||||||
Figure 4.11. Représentation type d’une expérience en parcelles divisées avec trois clones d’eucalyptus (v1, v2 et v3) (traitements des petites parcelles) et quatre niveaux d’azote (n0, n1, n2 et n3) (traitements des grandes parcelles, dans trois répétitions).
|
n3 |
n1 |
n0 |
n2 |
n1 |
n0 |
n5 |
n2 |
n0 |
n1 |
n2 |
n3 |
||
|
v2 |
v1 |
v1 |
v2 |
v1 |
v3 |
v3 |
v1 |
v4 |
v3 |
v3 |
v1 |
||
|
v1 |
v3 |
v2 |
v3 |
v3 |
v1 |
v2 |
v2 |
v2 |
v4 |
v2 |
v3 |
||
|
v3 |
v2 |
v3 |
v1 |
v2 |
v2 |
v1 |
v3 |
v1 |
v1 |
v4 |
v2 |
||
|
Répétition I |
Répétition II |
Répétition III |
|||||||||||
Le schéma d’un champ, dans une expérience en parcelles divisées (comme celle de la Figure 4.11) a quelques caractéristiques importantes: i) La taille de la grande parcelle est b fois plus grande que celle de la petite parcelle. Dans notre exemple, avec 3 variétés (b = 3) la grande parcelle est 3 fois plus grande que la petite ; ii) Chaque traitement de grande parcelle est testé r fois, alors que chaque traitement de petite parcelle est testé ar fois. Ainsi, les traitements des petites parcelles sont toujours testés un plus grand nombre de fois que ceux des grandes parcelles, ce qui explique leur plus grande précision. Dans notre exemple, chacun des 4 niveaux d’azote est testé trois fois, mais chacun des 3 clones est testé douze fois.
4.6.2. Analyse de variance
L’analyse de variance d’une expérience en parcelles divisées se fait en deux temps: l’analyse des grandes parcelles, et l’analyse des petites parcelles. Les calculs sont présentés à l’aide des données issues d’une expérience à deux facteurs sur les eucalyptus, comportant deux traitements sylvicoles (taille de la fosse) et 4 traitements d’engrais. Les données sur la hauteur des plants un an après la plantation sont reportées dans le Tableau 4.25.
Tableau 4.25. Données sur la hauteur (en cm) de plants d’ Eucalyptus tereticornis dérivées d’une expérience en parcelles divisées, menée en champ.
|
Hauteur (en cm) |
|||
|
Engrais |
Répétition I |
Répétition II |
Répétition III |
|
|
Taille de la fosse (30 cm x 30 cm x 30 cm) - p0 |
||
|
f0 |
25.38 |
61.35 |
37.00 |
|
f1 |
46.56 |
66.73 |
28.00 |
|
f2 |
66.22 |
35.70 |
35.70 |
|
f3 |
30.68 |
58.96 |
21.58 |
|
|
Taille de la fosse (40 cm x 40 cm x 40 cm) - p1 |
||
|
f0 |
19.26 |
55.80 |
57.60 |
|
f1 |
19.96 |
33.96 |
31.70 |
|
f2 |
22.22 |
58.40 |
51.98 |
|
f3 |
16.82 |
45.60 |
26.55 |
Notons A le facteur des grandes parcelles (taille de la fosse) et B, le facteur des petites parcelles (traitements d’engrais). Effectuer comme suit l’analyse de variance:
*Etape 1. Dresser une table préliminaire de l’analyse de variance d’un plan en parcelles divisées.
Tableau 4.26. Représentation schématique de l’analyse de variance d’un plan en parcelles divisées.
|
Source de |
Degré de liberté |
Somme des |
Carré moyen |
|
|
variation |
(df) |
carrés (SS) |
|
F calculé |
|
Répétition |
r - 1 |
SSR |
MSR |
|
|
A |
a - 1 |
SSA |
MSA |
|
|
Erreur (a) |
(r - 1)(a - 1) |
SSEa |
MSEa |
|
|
B |
b - 1 |
SSB |
MSB |
|
|
AB |
(a - 1)(b - 1) |
SSAB |
MSAB |
|
|
Erreur (b) |
a(r - 1)(b - 1) |
SSEb |
MSEb |
|
|
Total |
rab - 1 |
SSTO |
*Etape 2. Faire les deux tableaux des totaux suivants:
i) Tableau des totaux à deux entrées : répétition x facteur A, avec les totaux des répétitions, les totaux du facteur A et le total général: Dans notre exemple, le tableau des totaux ((RA)ki) répétitions x taille de la fosse, avec les totaux de la répétition (Rk), les totaux de la taille de la fosse (Ai) et le total général (G) calculés est présenté au Tableau 4.27.
Tableau 4.27. Tableau des totaux des hauteurs répétition x taille de la fosse, calculés à partir des données du Tableau 4.25
|
Taille de la fosse |
Rép. I |
Rép. II |
Rép. III |
(Ai) |
|
p0 |
168.84 |
222.74 |
122.28 |
513.86 |
|
p1 |
78.26 |
193.76 |
167.83 |
439.85 |
|
Total rép. (Rk) |
247.10 |
416.50 |
290.10 |
|
|
Total général (G) |
953.70 |
ii) Le tableau des totaux à double entrée facteur A x facteur B : Dans notre exemple, le tableau des totaux (AB) taille de la fosse x traitement d’engrais, avec le calcul des totaux des traitements d’engrais (Bj) est présenté au Tableau 4.28.
Tableau 4.28. Tableau des totaux des hauteurs taille de la fosse x traitement d’engrais, calculés à partir des données du Tableau 4.25
|
Traitement d’engrais |
||||||
|
Taille de la fosse |
f0 |
f1 |
f2 |
f3 |
||
|
p0 |
123.73 |
141.29 |
137.62 |
111.22 |
||
|
p1 |
132.66 |
85.62 |
132.60 |
88.97 |
||
|
Total (Bj) |
256.39 |
226.91 |
270.22 |
200.19 |
||
*Etape 3. Calculer comme suit le facteur de correction et les sommes des carrés, pour l’analyse des grandes parcelles. Notons yijk la réponse observée sur la i-ème grande parcelle, la j-ème petite parcelle, dans la k-ème répétition.
![]() (4.37)
(4.37)
= ![]()
SSTO = 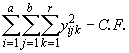
(4.38)
= [(25.38)2 + (46.56)2 + … + (26.55)2] - 37897.92
= 6133.10
SSR = 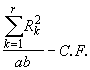 (4.39)
(4.39)
= ![]()
= 1938.51
SSA = 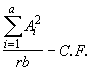 (4.40)
(4.40)
=![]()
= 228.25
SSEa =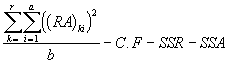 (4.41)
(4.41)
= ![]()
= 1161.70
*Etape 4. Calculer comme suit les sommes des carrés pour l’analyse des petites parcelles:
SSB = 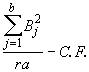 (4.42)
(4.42)
= ![]()
= 488.03
SSAB = 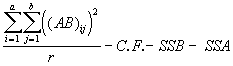 (4.43)
(4.43)
= ![]() - 37897.92 - 488.03 - 1161.70
- 37897.92 - 488.03 - 1161.70
= 388.31
SSEb = SSTO - SSR - SSA - SSB - SSAB-SSEa (4.44)
= 6133.10 - 1938.51 - 228.25 - 488.03 - 388.31
= 3090.00
*Etape 5. Pour chaque source de variation, calculer le carré moyen en divisant SS par le degré de liberté df qui lui est associé. La valeur de F de chaque effet à tester se calcule en divisant chaque carré moyen par le terme d’erreur correspondant (voir Tableau 4.26).
*Etape 6. Entrer dans le tableau d’analyse de variance toutes les valeurs obtenues de l’étape 3 à l’étape 5, comme indiqué dans le tableau 4.29; puis comparer chacune des valeurs calculées de F avec les valeurs tabulaires de F correspondantes, et indiquer si la différence est significative ou non, à l’aide de l’astérisque ou du signe approprié. Pour chaque effet dont la valeur calculée de F n’est pas inférieure à 1, chercher dans l’Annexe 3 la valeur tabulaire de F, avec f1 = df du MS du numérateur et f2 = df du MS du dénominateur, au seuil de signification déterminé au préalable. Par exemple, la valeur tabulaire de F pour tester l’effet AB est de 3.49 au seuil de signification de 5%, pour 3 et 12 degrés de liberté.
Tableau 4.29. Analyse de variance des données du Tableau 4.20 issues d’une expérience en parcelles divisées
|
Source de |
Degré de liberté |
Somme des |
Carré |
F |
F tabulaire |
|
variation |
carrés |
moyen |
calculé |
5% |
|
|
Répétition |
2 |
1938.51 |
969.26 |
||
|
A |
1 |
228.25 |
228.25 |
0.3930ns |
4.75 |
|
Erreur (a) |
2 |
1161.70 |
580.85 |
||
|
B |
3 |
488.03 |
162.68 |
0.6318ns |
3.49 |
|
AB |
3 |
388.31 |
129.44 |
0.5027ns |
3.49 |
|
Erreur (b) |
12 |
3090.00 |
257.50 |
||
|
Total |
23 |
37897.92 |
ns Non significatif au seuil de 5%
*Etape 7. Calculer les deux coefficients de variation relatifs à l’analyse des grandes parcelles et à l’analyse des petites parcelles.
![]() (4.45)
(4.45)
![]()
![]() (4.46)
(4.46)
= ![]()
La valeur de cv (a) indique le degré de précision associé au facteur des grandes parcelles. La valeur de cv(b) indique le degré de précision du facteur des petites parcelles et de son interaction avec le facteur des grandes parcelles. En principe, la valeur de cv(b) est inférieure à celle de cv(a) car, comme on l’a déjà indiqué, le facteur assigné aux grandes parcelles est généralement mesuré avec moins de précision que celui assigné aux petites parcelles. Dans notre exemple, cv(b) est inférieur à cv(a), mais les deux valeurs étaient suffisamment élevées pour masquer toute éventuelle différence des traitements, ce qui rend non significatifs tous les effets des facteurs dans l’analyse de la variance.
4.6.3. Comparaison de traitements
Dans une expérience en parcelles divisées, quatre types de comparaisons appariées sont possibles. Chacune doit avoir un ensemble de valeurs de la PPDS qui lui est propre. Ces comparaisons sont les suivantes :
Type-(1). Comparaisons entre deux moyennes de traitement des grandes parcelles, calculées sur tous les traitements des petites parcelles.
Type-(2). Comparaison entre deux moyennes de traitement des petites parcelles, calculées sur tous les traitements des grandes parcelles.
Type-(3). Comparaison entre deux moyennes de traitement de petites parcelles, par rapport au même traitement des grandes parcelles.
Type-(4). Comparaison entre deux moyennes des traitements des grandes parcelles, au niveau de traitements de petites parcelles similaires ou différents (ou moyennes de deux combinaisons de traitements quelconques)
Tableau 4.30 Erreur type de la différence moyenne pour chacun des 4 types de comparaisons de paires
|
Type de comparaison de paire |
|
|
|
Type-(1) : |
Entre deux moyennes de grandes parcelles (moyennes calculées sur tous les traitements des petites parcelles) |
|
|
Type-(2) : |
Entre deux moyennes de petites parcelles (moyennes calculées sur tous les traitements des grandes parcelles) |
|
|
Type-(3) : |
Entre deux moyennes de petites parcelles, au niveau du même traitement de grande parcelle |
|
|
Type-(4) : |
Entre deux moyennes de grande parcelle à des niveaux de traitements de petites parcelles égaux ou différents |
|
Note : Ea = MSEa, Eb = MSEb, r = nombre de répétitions, a = nombre de traitements de grande parcelle, et b = nombre de traitements de petites parcelles.
Lorsque le calcul de ![]() fait intervenir plus d’un terme d’erreur, comme c’est le cas dans les comparaisons de Type-(4), les valeurs tabulaires de t, tirées de l’Annexe 2 ne peuvent pas être utilisées telles quelles et il faut calculer des valeurs tabulaires pondérées de t. Dans ce cas ces valeurs sont données par la formule:
fait intervenir plus d’un terme d’erreur, comme c’est le cas dans les comparaisons de Type-(4), les valeurs tabulaires de t, tirées de l’Annexe 2 ne peuvent pas être utilisées telles quelles et il faut calculer des valeurs tabulaires pondérées de t. Dans ce cas ces valeurs sont données par la formule:
Valeur tabulaire pondérée de t = ![]() (4.47)
(4.47)
où ta est la valeur de t pour le df de l’erreur (a) et tb est la valeur de t pour le df de l’erreur (b).
A titre d’exemple, prenons l’expérience factorielle 2 x 4 dont les données sont reportées dans le Tableau 4.25. Bien que l’analyse de variance (Tableau 4.29) montre que les trois effets (c’est-à-dire les deux effets principaux et l’effet d’interaction) ne sont pas significatifs, imaginons pour illustrer notre exemple, qu’il existe une interaction significative entre la taille de la fosse et l’engrais. En d’autres termes, on suppose que l’effet de l’engrais varie avec la taille de la fosse. En pareil cas, la comparaison entre les moyennes des niveaux " taille de la fosse ", calculées par rapport à tous les niveaux d’engrais, ou entre les moyennes des niveaux d’engrais, calculées par rapport à tous les niveaux " taille de la fosse ", ne serait pas valide. Les comparaisons les plus appropriées seront celles entre les moyennes des engrais, pour des fosses de même taille, ou entre les moyennes des tailles des fosses, pour un même dosage d’engrais. Ainsi, les étapes de calcul de la PPDS, permettant la comparaison de deux moyennes afférentes aux petites parcelles, pour un même traitement de grande parcelle, sont les suivantes :
*Etape 1. Calculer l’erreur type de la différence entre moyennes, à l’aide de la formule applicable à la comparaison de Type-(3) du Tableau 4.30.
![]()
= ![]()
*Etape 2. Grâce à la formule ![]() , calculer la valeur de la PPDS (ou LSD) au seuil de signification de 5%, avec la valeur tabulaire de t correspondant à 12 degrés de liberté de l’erreur (b)
, calculer la valeur de la PPDS (ou LSD) au seuil de signification de 5%, avec la valeur tabulaire de t correspondant à 12 degrés de liberté de l’erreur (b)
![]()
*Etape 3. Dresser le tableau à double entrée (taille de la fosse x engrais) des moyennes des différences de hauteur, comme indiqué dans le Tableau 4.31. Comparer les différences de hauteur moyenne entre les niveaux d’engrais observées pour chaque taille de la fosse, avec la valeur de la PPDS (ou LSD) calculée à l’Etape 2, et identifiez le cas échéant les différences significatives.
Tableau 4.31. Différence entre la hauteur moyenne des plants d’eucalyptus, à quatre niveaux d’engrais pour une fosse ayant une taille de 30 cm x 30cm x 30 cm, sur la base des données du Tableau 4.25.
|
Différence de hauteur moyenne (en cm), à p0 |
||||
|
f0 |
f1 |
f2 |
f3 |
|
|
f0 |
0.00 |
-5.86 |
-4.63 |
4.17 |
|
f1 |
0.00 |
1.23 |
10.03 |
|
|
f2 |
0.00 |
8.80 |
||
|
f3 |
0.00 |
|||
|
Différence de hauteur moyenne (en cm), à p1 |
||||
|
f0 |
f1 |
f2 |
f3 |
|
|
f0 |
0.00 |
15.68 |
0.02 |
14.56 |
|
f1 |
0.00 |
-15.66 |
-1.12 |
|
|
f2 |
0.00 |
14.54 |
||
|
f3 |
0.00 |
|||
4.7. Plan en treillis
En théorie, les plans en blocs complets, comme les PEBAC, sont applicables à toutes les expériences quel que soit le nombre de traitements, toutefois, plus ils sont nombreux, moins ils sont efficaces car les blocs perdent leur homogénéité en raison de leur grande taille. Il existe un autre type de plans pour les expériences à un seul facteur comprenant un grand nombre de traitements. Ce sont les plans en blocs incomplets, dans lesquels, comme leur nom l’indique, chaque bloc ne contient pas tous les traitements, de sorte que les blocs peuvent être maintenus à une taille raisonnable, même si le nombre de traitements est élevé. Comme les blocs sont incomplets, la comparaison des traitements apparaissant ensemble dans un bloc est plus précise que celle des autres traitements. Cet inconvénient peut être contourné, sachant que dans le plan d’ensemble, chaque paire de traitement apparaît un nombre égal de fois dans un même bloc. On dit de ces plans qu’ils sont " équilibrés ", ou " compensés ". Etant donné qu’il faut un grand nombre de répétitions pour arriver à un équilibre complet, on peut opter pour un plan partiellement équilibré (ou partiellement compensé), dans lequel sont admis des degrés de précision variables selon les groupes de traitements qui sont comparés. Dans la catégorie des plans en blocs incomplets, on utilise souvent pour les expériences forestières des plans en treillis, dans lesquels le nombre de traitements est un carré parfait et les blocs peuvent être groupés en ensembles complets de répétitions. Les paragraphes qui suivent seront spécialement consacrés à l’étude spécifique des plans en treillis simple.
4.7.1. Plan en treillis simple
Les plans en treillis simple sont aussi appelés treillis doubles ou treillis carrés. Comme le nombre des traitements doit être un carré parfait, ces plans peuvent être construits pour 9, 16, 25, 36, 49, 64, 81, 121,…. traitements. Ils nécessitent deux répétitions et ne sont que partiellement équilibrés étant donné que les traitements sont répartis en deux groupes, et que la comparaison des traitements est plus ou moins précise suivant le groupe. Nous allons illustrer par un exemple la construction et la représentation schématique du plan, pour 25 traitements.
*Etape 1. Assigner au hasard un nombre de 1 à 25 à chaque traitement. Cette opération est nécessaire pour éviter tout type de variation d’origine inconnue affectant les effets des traitements.
*Etape 2. Disposer les nombres attribués aux traitements, de 1 à 25, de façon à former un carré, comme dans la Figure 4.12.
Figure 4.12. Disposition initiale des traitements dans un plan en treillis simple
|
1 |
2 |
3 |
4 |
5 |
|
6 |
7 |
8 |
9 |
10 |
|
11 |
12 |
13 |
14 |
15 |
|
16 |
17 |
18 |
19 |
20 |
|
21 |
22 |
23 |
24 |
25 |
*Etape 3. Regrouper les traitements par ligne. On obtient les groupes (1, 2, 3, 4, 5), (6, 7, 8, 9, 10), (11, 12, 13, 14, 15), (16, 17, 18, 19, 20) et (21, 22, 23, 24, 25). A présent, chaque bloc constitue un groupe de traitements assigné à un bloc et les cinq blocs ainsi formés constituent une répétition complète. Cette méthode de groupement par lignes est généralement connue sous le nom de groupement-X ou groupement -A.
*Etape 4. Grouper les traitements par colonne. Les groupes ainsi formés sont (1, 6, 11, 16, 21), (2, 7, 12, 17, 22), (3, 8, 13, 18, 23), (4, 9, 14, 19, 24) et (5, 10, 15, 20, 25). A présent chaque bloc constituera un groupe de traitements assigné à un bloc et les cinq blocs forment une répétition complète. Cette méthode de groupement par colonnes est généralement connue sous le nom de groupement-Y ou groupement-B.
Les deux groupements-X et Y garantissent que deux traitements qui sont apparus ensemble une fois dans un même bloc ne s’y retrouveront plus simultanément. Avant la procédure de randomisation, les deux ensembles de groupements qui viennent d’être décrits se présentent, comme dans Figure 4.13.
Figure 4.13. Deux répétitions d’un plan en treillis simple, avant la randomisation
R& eacute;pétition I (groupement-X)
|
Bloc No. 1 |
1 |
2 |
3 |
4 |
5 |
|
Bloc No. 2 |
6 |
7 |
8 |
9 |
10 |
|
Bloc No. 3 |
11 |
12 |
13 |
14 |
15 |
|
Bloc No. 4 |
16 |
17 |
18 |
19 |
20 |
|
Bloc No. 5 |
21 |
22 |
23 |
24 |
25 |
Répétition II (groupement-Y)
|
Bloc No.6 |
1 |
6 |
11 |
16 |
21 |
|
Bloc No.7 |
2 |
7 |
12 |
17 |
22 |
|
Bloc No.8 |
3 |
8 |
13 |
18 |
23 |
|
Bloc No.9 |
4 |
9 |
14 |
19 |
24 |
|
Bloc No.10 |
5 |
10 |
15 |
20 |
25 |
*Etape 5. Dans chaque répétition, les groupes de traitements sont répartis au hasard à l’intérieur des différents blocs. On pratique une randomisation distincte pour chaque répétition. L’allocation des traitements aux parcelles, à l’intérieur de chaque bloc, se fait aussi de manière aléatoire. La randomisation est pratiquée séparément pour chaque groupe, de manière indépendante pour chaque répétition. Enfin, lorsque l’on conçoit le dispositif des répétitions sur le terrain, il faut aussi allouer au hasard dans le champ les positions des répétitions X et Y. Cette procédure d’allocation des traitements et des répétitions garantit l’élimination de tous types de variations systématiques inconnues affectant les effets des traitements. A l’issue de la randomisation complète, le plan effectif pourrait se présenter comme indiqué dans la Figure 4.14.
Figure 4.14. Représentation d’un plan en treillis simple randomisé
|
Bloc No. 5 |
25 |
24 |
21 |
23 |
22 |
|
Bloc No. 4 |
20 |
19 |
18 |
17 |
16 |
|
Bloc No. 1 |
5 |
4 |
1 |
3 |
2 |
|
Bloc No. 3 |
13 |
14 |
15 |
12 |
11 |
|
Bloc No. 2 |
6 |
9 |
7 |
10 |
8 |
|
Bloc No. 6 |
16 |
6 |
1 |
21 |
11 |
|
Bloc No. 9 |
19 |
4 |
9 |
14 |
24 |
|
Bloc No. 7 |
7 |
2 |
17 |
22 |
12 |
|
Bloc No. 10 |
5 |
20 |
25 |
10 |
15 |
|
Bloc No. 8 |
23 |
3 |
8 |
18 |
13 |
Si, dans chaque répétition, les blocs sont contigus, on pourra, dans certaines conditions, analyser toute l’expérience comme s’il s’agissait d’un PEBAC. On a déjà précisé qu’un plan en treillis simple nécessitait au moins deux répétitions, l’une avec le groupement X, l’autre avec le groupement Y des traitements. Si l’on juge préférable de faire plus de deux répétitions, on choisira un nombre pair, car les deux groupes (X et Y) devront être répétés le même nombre de fois. L’allocation des traitements se fait selon la procédure précédente.
4.7.2. Analyse de variance pour un plan en treillis simple
Dans le cas d’un plan de base en treillis simple répété une seule fois, les étapes de l’analyse de la variance sont décrites dans les passages qui suivent, avec les vérifications par le calcul, le cas échéant. Le matériel utilisé pour notre démonstration est extrait d’une expérience réalisée à Vallakkadavu, dans le Kerala (Inde), et portait sur 25 clones d’Eucalyptus grandis.
Le Tableau 4.32 montre la disposition effective du champ, avec les positions des blocs et l’allocation des traitements à l’intérieur de chaque bloc, à l’issue de la procédure de randomisation. Le chiffre inscrit dans le coin supérieur gauche de chaque case est le numéro d’identification du clone, alors que le chiffre figurant dans le coin inférieur droit se réfère à la hauteur moyenne des arbres de la parcelle, un an après la plantation. L’analyse de variance implique un ajustement des sommes des carrés des traitements et des blocs, étant donné que les blocs sont incomplets. Cet ajustement ne serait pas nécessaire pour des plans en blocs complets.