Tableau 4.32. Schéma d’un plan en treillis double 5 x 5 montrant la croissance en hauteur (en cm) de clones d’Eucalyptus grandis.

Répétition - I

Répétition - II

*Etape 1. Disposer de façon systématique les blocs dans chaque groupe (groupes X et Y) et les traitements dans chaque bloc, conformément aux observations, comme dans le Tableau 4.33.

Tableau 4.33. Arrangement systématique des blocs et des traitements à l’intérieur des blocs du Tableau 4.32.

Répétition - I (groupe X)

Répétition - II (groupe Y)

*Etape 2. Dresser le tableau des totaux des traitements en additionnant les rendements de chaque clone, obtenus dans les deux répétitions (voir Tableau 4.34). Ces totaux ne sont ajustés à aucun effet de bloc.

Tableau 4.34. Totaux des traitements (clone)

*Etape 3. Calculer les totaux de tous les blocs B₁, B₂, …, B₁₀ en sommant les observations apparaissant dans chaque bloc. Par exemple, le total B₁ du premier bloc est donné par

B₁ = 136.70+113.50+123.60+122.50+158.00 = 654.30

Calculer le total de chaque répétition en sommant les totaux des blocs dans chaque répétition. Pour la répétition I,

R₁ = B₁ + B₂ + B₃+ B₄+ B₅ (4.48)

= 654.30 + 594.20 + 565.60 + 553.30 + 587.10

= 2954.50

Calculer le total général G = R₁ + R₂ (4.49)

= 2954.50 + 3176.00

= 6130.50

*Etape 4. Dresser un schéma préliminaire de la table d’analyse de la variance du treillis simple.

Tableau 4.35. Représentation schématique de la table d’analyse de la variance d’un treillis simple

*Etape 5. Trouver la somme totale des carrés, la somme des carrés des répétitions et celles des traitements non ajustés. A cette fin, calculer d’abord le facteur de correction (C.F.).

C. F. = (4.50)

où n = rk²

r = Nombre de répétitions

k² = Nombre de traitements

k = Nombre de parcelles dans un bloc

C. F. = = 751660.61

Pour la somme totale des carrés, trouver la somme des carrés de toutes les observations de l’expérience et soustraire le facteur de correction.

SSTO = (4.51)

= { (136.70)² + (113.50)² +……..+ (137.60)² } - C. F.

= 770626.43 - 751660.61 = 18965.83

Calculer la somme des carrés des répétitions

SSR = (4.52)

= 751660.61

= 752641.85 - 751660.61 = 981.245

Calculer la somme des carrés des traitements non ajustés

SST (non aj.) = 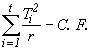(4.53)

=

= 760747.90 - 751660.61 = 9087.29

*Etape 6. Calculer pour chaque bloc, dans la répétition 1 (groupe X), un total ajusté C_b en soustrayant chaque total de bloc de la répétition 1 du total de la colonne correspondante de la répétition II (groupe Y), qui contient le même ensemble de variétés (voir Tableau 4.36). De la même manière, calculer pour chaque bloc de la répétition II, un total ajusté en soustrayant chaque total de bloc de la répétition II du total de la colonne correspondante de la répétition I (groupe X), contenant le même ensemble de variétés (voir Tableau 4.37). Faire le total des valeurs C_b pour chaque répétition et vérifier si leur somme est nulle.

Total des valeurs C_b pour la Répétition I = U₁ = 221.50

Total des valeurs C_b pour la Répétition II = U₂ = -221.50

Cette vérification garantit l’exactitude arithmétique des calculs des étapes précédentes.

Tableau 4.36. Calcul des valeurs de C_b pour les blocs de la Répétition I

Tableau 4.37. Calcul des valeurs de C_b pour les blocs de la Répétition II

La somme des carrés des blocs ajustés est donnée par la relation:

SSB (aj.) = 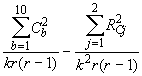(4.54)

où r = Nombre de répétitions,

k = Nombre de traitements par bloc.

SSB (aj.) =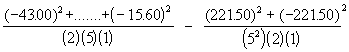

= 3782.05 - 1962.49 = 1819.56

Pour finir, la somme des carrés des erreurs s’obtient par soustraction

SSE = SSTO - SSR - SST (non-aj.) - SSB (aj.) (4.55)

= 18965.83 - 981.24 - 9087.29 - 1819.56

= 7077.73

Remarquons que la somme des carrés due à l’erreur (SSE) calculée ici représente la part de la variation (de la variable de réponse) entre les parcelles à l’intérieur de chaque bloc qui est causée par des facteurs externes non contrôlés. Elle est donc généralement appelée variance (ou erreur) intrabloc, alors que la somme des carrés des blocs ajustés est la variance interbloc (ou entre blocs).

*Etape 7. Après avoir obtenu les différentes sommes des carrés, insérer tous les résultats dans la table d’analyse de la variance (Tableau 4.38). Les carrés moyens s’obtiennent, comme d’habitude, en divisant les sommes des carrés par les degrés de liberté.

Tableau 4.38. Table d’analyse de variance d’un treillis simple, à l’aide des données du Tableau 4.32.

Le carré moyen des traitements figurant dans la table d’analyse de variance (Tableau 4.38) n’est pas ajusté aux effets de bloc. Or, on a déjà signalé que les moyennes des traitements ne sont pas exemptes de ces effets. Il s’ensuit que le test F fourni par l’analyse de la variance n’est pas valide pour détecter les différences de traitements. Avant d’appliquer le test F, il faut donc ajuster les moyennes des traitements compte tenu des effets de bloc et calculer la somme ajustée des carrés des traitements. Pour ce faire, on suit la procédure décrite dans l’étape 9. Cette procédure peut être adoptée si les circonstances l’exigent, mais elle impose des calculs supplémentaires qui, sauf indication contraire, peuvent être évités. Par exemple, dans un essai en champ comprenant un grand nombre de traitements, on peut en général s’attendre à trouver une différence significative entre les moyennes des traitements. A partir des résultats du Tableau 4.38, on peut effectuer l’analyse préliminaire applicable à un PEBAC, test moins sensible aux différences des traitements.

*Etape 8. Analyse préliminaire d’un PEBAC: Pour obtenir la somme des carrés des erreurs, on commence par additionner l’erreur interbloc et l’erreur intrabloc, puis on complète comme suit la table de l’analyse de variance :

Erreur totale= Erreur Interbloc + Erreur Intrabloc (4.56)

= 1819.56 + 7077.73

= 8897.29

Tableau 4.39. Table d’analyse de variance pour une analyse préliminaire d’un PEBAC.

La valeur observée de F (1.02) obtenue en divisant le carré moyen des traitements par le carré moyen de l’erreur totale, est inférieure à la valeur tabulaire de F (1,98) au seuil de signification de 5% pour (24, 24) degrés de liberté. On en déduit qu’il n’y a pas de différence significative entre les traitements, au seuil de 5%. L’analyse PEBAC préliminaire ayant donnè une valeur non-significative de F, on doit effectuer un test F plus approprié, en ajustant les sommes des carrés des traitements aux effets de bloc, car cette procédure ne peut qu’augmenter la sensibilité du test. Pour effectuer cet ajustement de la somme des carrés des traitements en vue d’obtenir un test F plus approprié pour détecter les différences de traitements, on suivra la procédure de l’étape 9.

*Etape 9. Calculer les sommes des carrés des traitements ajustées aux effets de bloc: obtenir d’abord la somme des carrés des blocs non ajustés à l’intérieur des répétitions. Les sommes B₁, B₂, …, B₁₀ des blocs ayant déjà été calculées à l’étape 3, les calculs restants sont facilités:

SS de bloc non ajusté pour la répétition I = SSB₁(non aj.)

= (4.57)

=

= 1219.75

SS de bloc non ajusté pour la répétition II = SSB₂ (non aj.)

= (4.58)

=

= 1850.83

Pour finir, calculer la somme totale des carrés des blocs non ajustés SSB (non aj.)

SSB (non aj.) = SSB₁(non aj.) + SSB₂ (non aj.) (4.59)

= 1219.75 + 1850.83 = 3070.58

Calculer la quantité de correction Q suivante, à retrancher de la somme des carrés des traitements non ajustés:

Q = 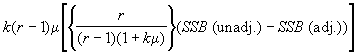(4.60)

où m = (4.61)

où E_b = Carré moyen interbloc ajusté

E_e = Carré moyen intrabloc

Dans notre exemple, m =

= - 0.189

Q =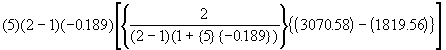

= -42989.60

Pour finir, soustraire cette quantité Q de la somme des carrés des traitements non ajustée pour obtenir leur somme des carrés ajustée.

SST (aj) = SST (non aj.) - Q (4.62)

= 9087.29 - (-42989.60) = 52076.89

Dresser la table d’analyse de variance suivante pour tester la signification des effets des traitements.

Tableau 4.40. Table d’analyse de variance pour tester la signification des moyennes ajustées des traitements.

Dans cet exemple, la valeur calculée de F s’avère significative au seuil de signification de 5%, ce qui indique des différences significatives entre les traitements. La sensibilité du test F est plus grande après l’élimination des effets de bloc. Bien qu’il n’en soit pas ainsi dans notre exemple, on part généralement du principe que l’effet de bloc, estimé par la valeur E_b, est supérieur à l’erreur intrabloc E_e.

Les moyennes des traitements doivent également être ajustées, car les moyennes des traitements ordinaires ne sont pas des estimations sans biais de leurs valeurs réelles. Pour effectuer ces ajustements en vue d’éliminer les effets de bloc, on procède comme suit:

*Etape 10. Calculer un terme de correction pour chaque bloc, en multipliant chaque valeur C_b par la quantité m ( -0.189), donnée par (4.61).

Pour la répétition I, ces valeurs sont:

m C₁ = -8.13, m C₂= -4.74, m C₃ = 6.01, m C₄ = -14.78, m C₅ = -20.22

et pour la répétition II:

m C₆ =18.99, m C₇ = 14.59, m C₈ = 3.74, m C₉ =1.59, m C₁₀ = 2.95

Insérer ces valeurs dans la dernière ligne et la dernière colonne du Tableau 4.34, d’après le modèle du Tableau 4.41. Vérifier que la somme de toutes les valeurs m C_b est nulle, si l’on excepte l’arrondissement de l’erreur:

m C₁ + m C₂ + …+ m C₁₀= -8.13+-4.74 +…+ 2.95= 0.00

Entrer les valeurs m C_b de la répétition I dans l’avant- dernière colonne du Tableau 4.41 et les valeurs de m C_b de la répétition II, dans l’avant-dernière ligne de ce même tableau. En écrivant ainsi les valeurs des corrections à apporter aux totaux non ajustés des traitements, on évitera de nombreuses erreurs de calculs. Chaque total de traitement inscrit dans le Tableau 4.41 doit à présent être ajusté pour tenir compte des effets des blocs, en apportant les corrections voulues aux blocs dans lesquels apparaît le traitement considéré..

Tableau 4. 41. Totaux des traitements et facteurs de correction.

Par exemple, le clone 1 apparaît dans le Bloc 1 de la Répétition 1 et dans le bloc 6 de la Répétition 2. Ajouter les valeurs de m C₁ et m C₆ au total du clone 1:

Total des traitements ajusté, pour le clone 1 = 260.80 -(-8.13) - 18.99 = 2.55

Etant donné que les corrections des blocs ont déjà été insérées dans le Tableau 4.41, les totaux ajustés des traitements correspondent simplement aux valeurs respectives de m C_b, dans la colonne et la ligne où apparaît ce traitement. Pour finir, dresser un tableau faisant apparaître le total des traitements ajusté aux effets de bloc. Les valeurs ajustées sont reportées dans le Tableau 4.42 ci-dessous.

Tableau 4.42. Totaux ajustés des traitements

Déterminer les moyennes des traitements ajustées en divisant chaque valeur par 2 puisque chaque total contient deux observations tirées de 2 répétitions (Tableau 4.43)

Tableau 4.43. Moyennes ajustées des traitements

On a déjà vu que, dans un treillis partiellement équilibré, les traitements qui apparaissent dans le même bloc sont comparés avec plus de précision (c’est à dire avec une erreur-type moindre) que ceux qui se trouvent dans des blocs différents.

L’erreur-type accompagnant la comparaison des moyennes de deux traitements quelconques apparaissant ensemble dans le même bloc est donnée par la formule:

(4.63)

où m =

E_b = Carré moyen interbloc

E_e = Carré moyen intrabloc

r = Nombre de répétitions

Dans notre exemple,

= 18.9408

L’erreur type de la comparaison des moyennes des traitements apparaissant dans des blocs différents est,

(4.64)

Dans notre exemple,

16.5875

Ici, . Ceci est uniquement lié aux données spécifiques de notre exemple, et ne saurait être considéré comme le cas courant.

En multipliant ces erreurs-type par la valeur tabulaire du test t, pour les degrés de liberté des erreurs intrabloc au seuil de signification spécifié, on obtiendra la valeur de la PPDS à l’aide de laquelle on pourra comparer les moyennes ajustées des traitements pour détecter des différences significatives.

4.8. Plans de surface de réponse

Dans les expériences dans lesquelles un ou plusieurs facteurs quantitatifs sont testés à plusieurs niveaux, on a souvent intérêt à résumer les données en ajustant un modèle adéquat décrivant la relation facteur-réponse. Ces facteurs quantitatifs peuvent être de divers ordres: engrais, irrigation, densité de peuplement etc..., et la finalité de l’expérience peut être de déterminer l’influence des niveaux de ces facteurs sur la réponse, g . On peut représenter la réponse g comme une fonction appropriée des niveaux x_1u, x_2u,.. ., x_ku des k facteurs et de b , l’ensemble des paramètres. Prenons l’exemple d’un modèle classique:

g _u = f (x_1u, x_2u, …, x_ku ; b ) + e_u (4.65)

où u = 1, …, t représente les N observations et x_iu le niveau du i-ème facteur (i = 1, 2, …, k) dans la u-ème observation. Le résidu e_u mesure l’erreur expérimentale dans la u-ème observation. La fonction f est appelée surface de réponse. Lorsque l’on connaît f , on dispose d’une synthèse complète des résultats de l’expérience, et il est plus facile de trouver la combinaison optimale des dosages. On peut en outre estimer la réponse pour des valeurs de x_iu qui ne sont pas testées dans le cadre de l’expérience. Les dispositifs spécifiquement conçus pour ajuster la surface des réponses sont appelés plans de surface de réponse. Les surfaces de réponse sont habituellement estimées par des polynômes de degré approprié, le plus courant étant le polynôme de second degré. Nous concentrerons donc notre attention sur les plans se prêtant à l’ajustement de ce type de polynôme.

Soient k facteurs tels que le i-ème ait s_i niveaux. En tout, on aura s_ix s₂x…….x s_k combinaisons de traitements dont on tirera t combinaisons pour ajuster une fonction du second degré de la forme

(4.66)

où y_u est la réponse obtenue à partir de la u-ème combinaisons de facteurs (u = 1, 2, …, t)

x_iu est le niveau du i-ème facteur dans la u-ème observation

b ₀ est une constante

b _i est le i-ème coefficient de régression linéaire

b _ii est le i-ème coefficient de régression quadratique

b _ij est le (i,j)-ème coefficient d’interaction

e_u est la composante de l’erreur aléatoire, de moyenne nulle et de variance constante, associée à la u-ème observation.

Prenons par exemple le cas particulier d’un modèle (4.66) englobant seulement deux facteurs,

Un plan de surface de réponse du second ordre permet un ajustement efficace de la relation facteur-réponse, par un polynôme de second degré. Lorsque l’on choisit les points du plan, on impose certaines contraintes aux niveaux des facteurs, de manière à simplifier l’estimation des paramètres et à conférer au plan obtenu et au modèle qui en découle les propriétés voulues, notamment le caractère rotatif ou tournant. Dans les plans rotatifs, la variance de la réponse estimée à partir d’une quelconque combinaison de traitements est une fonction de la somme des carrés des niveaux des facteurs dans la combinaison de traitements considérée. En d’autres termes, un plan d’expérience est dit rotatif (ou tournant) si la variance de la réponse estimée pour un ensemble donné de x valeurs dépend uniquement de la distance du point défini par les x valeurs au centre du plan, et pas de la direction. Les conditions suivantes doivent être vérifiées pour que les n points du plan constituent un plan rotatif de second ordre (PRSO).

(i) ,

. (4.67)

(ii) tl ₂ (4.68)

(iii) 3tl ₄ (4.69)

(iv) tl ₄ for i ¹ j or for i ¹ j (4.70)

(v) (4.71)

Nous allons décrire dans cette section l’une des méthodes les plus couramment employées pour construire un PRSO, qui débouche sur une classe de plans appelés plans composites centraux. Supposons que l’on ait k facteurs. Un plan composite central est un plan factoriel 2^k , ou un plan factoriel fractionné, (accompagné de la notation usuelle ± 1) augmenté des 2k points axiaux, (± a , 0, 0,…, 0), (0, ± a , 0,…, 0), (0,0,± a , 0,…,0), …, (0,0,0,…,± a ) et des n_c points centraux (0,0,…, 0). Dans le cas où l’on choisit un plan factoriel fractionné pour le premier ensemble de 2^k points, avec k > 4, il faut s’assurer que les contrastes déterminants n’impliquent pas d’interaction avec moins de cinq facteurs. Un plan composite central pour k = 3 est représenté ci-après. Ce plan est fait de 2³ = 8 points factoriels, (2)(3) = 6 points axiaux et 1 point central, soit quinze points au total.

x₁ x₂ x₃

-1 -1 -1

-1 -1 +1

-1 +1 -1

-1 +1 +1

+1 -1 -1

+1 -1 +1

+1 +1 -1

+1 +1 +1

+a 0 0

-a 0 0

0 +a 0

0 -a 0

0 0 +a

0 0 -a

0 0 0

Le caractère rotatif d’un plan composite central est déterminé par le choix de a . La valeur de a dépend du nombre de points dans la portion factorielle du plan. En effet, a = (n_f)^1/4 donne un plan composite central rotatif, où n_f est le nombre de points utilisés dans la portion factorielle du plan. Dans notre exemple, la portion factorielle contient n_f = 2³ = 8 points. Ainsi, on obtient un plan rotatif si la valeur de a = (8)^1/4 = 1.682. On trouvera des détails supplémentaires et des exemples de PRSO dans Das et Giri (1979) et Montgomery (1991).

Les combinaisons de traitements établies par un PRSO peuvent être essayées avec un nombre suffisant de répétitions, dans le cadre d’un plan d’expérience standard quelconque suivant la procédure de randomisation normale. Un plan de surface de réponse est donc uniquement un moyen particulier de sélectionner la combinaison de traitements dans une expérience factorielle, et non un plan, servant à représenter schématiquement une expérience.

Nous allons maintenant décrire l’analyse des données provenant d’un PRSO établi dans le cadre d’un plan entièrement randomisé. Supposons que, dans une expérience, le plan soit constitué de t points distincts, le g-ème point étant répété n_g fois. On note y_gu la réponse obtenue dans la u-ème répétition du g-ème point du plan et x_igu le niveau du i-ème facteur dans la u-ème répétition du g-ème point (i = 1,…, k ; g = 1,…, t ; u = 1,…n_g). Soit n le nombre total d’observations et (p+1) le nombre de paramètres dans le modèle du second ordre devant être ajusté.

Nous illustrerons l’analyse à l’aide de données provenant d’un essai de culture en pots. Pour simplifier, nous avons apporté quelques modifications aux données et à la structure du plan, de sorte que l’ensemble de données est dans une certaine mesure hypothétique. Cet exemple permet cependant de bien comprendre la procédure. L’expérience englobait trois facteurs: la quantité d’azote (N), de phosphore (P) et de potassium (K), respectivement appliqués sous forme d’urée, de superphosphate et de chlorure de potassium. Les unités expérimentales étaient des pots contenant chacun une plantule de roseau (Calamus hookerianus) de deux ans. Au cours de l’expérience, les quantités de N, P et K allaient de 5 à 20 g par pot. La structure des traitements était conforme au plan central composite décrit dans la Section 4.8.1, le schéma proprement dit étant un PER avec deux répétitions. Comme a =1.682 était le plus haut niveau codé dans le plan, les autres niveaux (ou doses) s’obtiennent en prenant pour a la valeur de 20g. Les autres doses sont donc (-a ) = 5g, (-1) = g , (0) =12.5g, , (+1) =g, (a ) = 20g. Les données, obtenues au terme d’une expérience de 2 ans, sur le poids séché à l’étuve d’une pousse, sont reportées dans le Tableau 4.44.

Tableau 4.44. Données sur le poids séché à l’étuve d’une pousse, au terme d’une expérience de deux ans

L’analyse se déroule selon les étapes suivantes

*Etape 1. Calculer les valeurs de et à l’aide des Equations (4.68) et (4.69).

15= 13.65825

= 0.9106

3t = 24.00789

= 0.5335

Conformément à la notation adoptée dans les équations (4.68) et (4.69), t est le nombre de points distincts dans le plan.

*Etape 2. Dresser le schéma préliminaire de la table d’analyse de la variance

Tableau 4.45. Représentation schématique de la table d’analyse de variance pour l’ajustement d’un PRSO.

*Etape 3. Calculer le facteur de correction (C.F.)

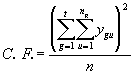(4.72)

= 2873.37

*Etape 4. Calculer la somme totale des carrés:

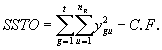(4.73)

= 55.43

*Etape 5. Calculer les estimations des coefficients de régression

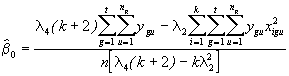(4.74)

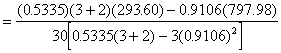
= 10.47

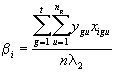(4.75)

= 0.92

= 0.54

= 0.55

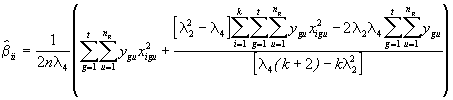(4.76)

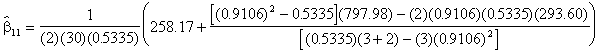
= - 0.50

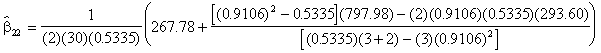
= - 0.20

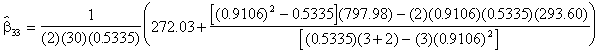
= - 0.06

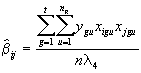(4.77)

= - 0.02

= 0.07

= 0.21

*Etape 6. Calculer la somme des carrés de la régression (SSR)

SSR =

(4.78)

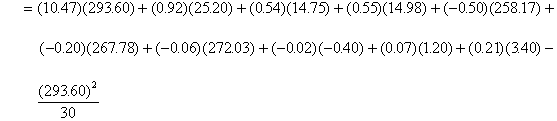
= 44.42

*Etape 7. Calculer la somme des carrés dus à l’erreur pure

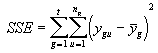(4.79)

= 9.9650

*Etape 8. Calculer la somme des carrés du manque d’ajustement avec la relation,

SSL = SSTO - SSR - SSE (4.80)

= 55.4347 - 44.4232 - 9.650

= 1.0465

*Etape 9. Insérer les différentes sommes des carrés dans la table d’analyse de la variance et calculer les différents carrés moyens en divisant les sommes des carrés par leurs degrés de liberté.

Tableau 4.46. Table d’analyse de la variance pour l’ajustement d’un PRSO, d’après les données du Tableau 4.44

*Etape 10. Calculer la valeur de F pour tester la signification du manque d’ajustement, pour détecter d’éventuelles erreurs de spécification du modèle.

(4.81)

Si le manque d’ajustement est significatif, le carré moyen de la régression est testé par rapport au carré moyen du manque d’ajustement. Dans le cas contraire, il est testé par rapport au carré moyen de l’erreur pure.

Dans notre exemple, F = = 0.3150

Ici, le manque d’ajustement n’est pas significatif. On peut donc tester le carré moyen de la régression par rapport au carré moyen de l’erreur pure. La valeur de F servant à tester la signification de la régression est

(4.82)

=

= 7.4299

Cette valeur de F est significative, si on la compare avec sa valeur tabulaire, qui est de 2,56, pour 9 et 15 degrés de liberté, au seuil de signification de 5 %. Le rapport de la somme des carrés de la régression à la somme totale des carrés indique que le modèle explique près de 80 % des variations de la variable de réponse.

*Etape 11. Les variances et les covariances des coefficients estimés sont donnés par les relations,

(4.83)

=

= 0.3283

où E = Carré moyen de l’erreur pure dans la table d’analyse de la variance.

(4.84)

=

= 0.0243

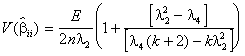(4.85)

=

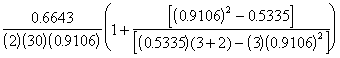
= 0.03

(4.86)

=

(4.87)

=

= -0.11

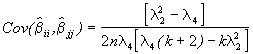(4.88)

=

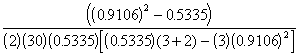
= 0.05

Toutes les autres covariances sont nulles.

La fonction de réponse ajustée est donc,

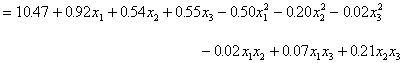
La surface sert entre autres à trouver la combinaison optimale des doses, pour laquelle la réponse est maximale ou économiquement optimale. De plus, l’équation ajustée est utile pour analyser la nature de la surface, dans des intervalles donnés des variables d’entrée. Etant donné que l’étude de ces aspects demande une connaissance de techniques mathématiques avancées, elle ne sera pas abordée ici, mais les lecteurs qui souhaitent approfondir cette question, peuvent se référer à Montgomery (1991).