Tableau 5.3. Illustration des paramètres d’estimation dans un système d’échantillonnage stratifié

*Etape 1. Calculer les quantités suivantes

N = (29 + 16 + 24) = 69

n = (10 + 5 + 8) = 23

= 4.215, = 4.422, = 5.458

!PAGEBREAK!

*Etape 2. Estimer la moyenne de la population à l’aide de l’équation (3)

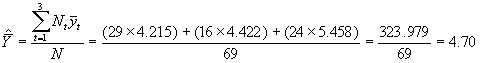
*Etape 3. Estimer la variance de à l’aide de l’équation (5)

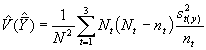
Dans cet exemple,

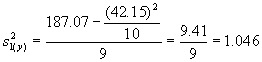
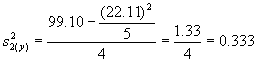
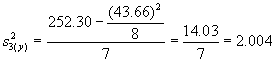
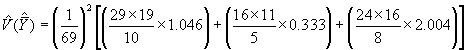
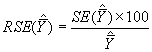(5.29)

Ignorons à présent les strates et supposons que le même échantillon de taille n = 23 formait un échantillon aléatoire simple prélevé dans la population de N = 69. L’estimation de la moyenne de la population se réduira alors à

L’estimation de la variance de la moyenne est alors

où

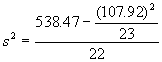
d’où

Le gain de précision due à la stratification se calcule comme suit

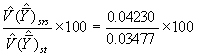
= 121.8

Le gain de précision est donc de 21.8%.

5.5. Echantillonnage à plusieurs degrés

En vue de réduire les coûts et/ou de concentrer les opérations en champ autour de certains points et, dans le même temps, d’obtenir des estimations précises, l’échantillonnage se fait parfois en plusieurs étapes. La procédure consistant à commencer par sélectionner des unités de grande taille puis à choisir un nombre déterminé de sous-unités dans les grandes unités, est connue sous le nom de sous-échantillonnage. Les grandes unités prennent le nom d’"unités du premier degré" ou "d’unités primaires" alors que les sous-unités sont appelées "unités du deuxième degré" ou "unités secondaires". La procédure peut aisément être généralisée aux échantillons à trois ou à plusieurs degrés. Par exemple, l’échantillonnage d’une étendue de forêt peut être effectué en trois étapes, premièrement en sélectionnant un échantillon de compartiments (unités du premier degré), puis un échantillon de sections topographiques (unités du deuxième degré) dans chaque compartiment sélectionné, et enfin en prélevant, dans chaque section topographique sélectionnée, un certain nombre de parcelles-échantillons de taille et de forme déterminées (unités du troisième degré).

Le système d’échantillonnage à plusieurs degrés a l’avantage de concentrer l’échantillon autour de plusieurs "points échantillons", au lieu de le disperser sur l’ensemble de la surface considérée dans l’enquête. Ceci réduit considérablement le coût des opérations et contribue à réduire les erreurs non liées à l’échantillonnage, grâce à une supervision efficace. De plus, dans les enquêtes forestières il arrive souvent que l’on dispose d’informations détaillées pour des groupes d’unités d’échantillonnage, mais par pour des unités individuelles. Par exemple, on peut avoir une liste de compartiments avec des détails sur la surface, alors que l’on n’a pas d’informations détaillées sur les sections topographiques dans chaque compartiment. C’est pourquoi, si les compartiments sont sélectionnés en tant qu’unités du premier degré, il peut être possible de collecter des données détaillées sur les sections topographiques, uniquement pour certains compartiments, et partant, d’utiliser un système d’échantillonnage à deux degrés sans tenter de dresser une carte des sections topographiques dans tous les compartiments. Le système d’échantillonnage à plusieurs degrés permet donc d’utiliser une base de sondage incomplète de toutes les unités d’échantillonnage et d’exploiter comme il convient et à bon escient les informations déjà disponibles, à chaque stade.

La sélection opérée à chaque stade peut être faite à l’aide d’une méthode d’échantillonnage aléatoire simple ou de toute autre méthode d’échantillonnage probabiliste, et l’on peut employer une méthode différente à chaque stade. Par exemple, on peut choisir un échantillon aléatoire simple de compartiments et opter pour un sondage systématique de parcelles en ligne ou en bandes, avec une origine choisie au hasard dans les compartiments sélectionnés.

Si les deux étapes de la sélection se font par échantillonnage aléatoire simple, la méthode prend le nom d’échantillonnage aléatoire simple à deux degrés. Par exemple, pour estimer le poids de l’herbe dans une superficie forestière, faite de 40 compartiments, les compartiments peuvent être considérés comme des unités d’échantillonnage primaires. Sur ces 40 compartiments, n = 8 compartiments peuvent être choisis au hasard au moyen d’une procédure d’échantillonnage aléatoire simple (voir Section 5.2.1). Un échantillon aléatoire de parcelles, égales en nombre ou non, peut être sélectionné dans chaque compartiment pour mesurer la quantité d’herbe, grâce à la procédure de sélection d’un échantillon aléatoire simple. On peut ensuite calculer les estimations de la quantité moyenne ou totale d’herbe disponible dans la superficie forestière, à l’aide des formules appropriées.

Soient une population constituée de N unités du premier degré et M_i le nombre d’unités du second degré dans la i-ème unité du premier degré. Supposons que n unités du premier degré soient sélectionnées et que, dans la i-ème unité du premier degré sélectionnée, on choisisse m_i unités du second degré pour former un échantillon de unités. Notons y_ij la valeur du caractère pour la j-ème unité du second degré dans la i-ème unité du premier degré.

Un estimateur non biaisé de la moyenne de la population 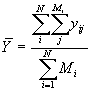s’obtient grâce à l’équation (5.30).

(5.30)

où 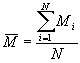. (5.31)

L’estimation de la variance de est donnée par la relation

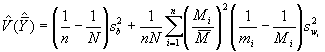(5.32)

où 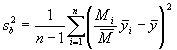(5.33)

(5.34)

Ici, on remarque que la variance de est composée de deux éléments. Le premier est une mesure de la variation entre les unités du premier degré et l’autre est une mesure de la variation à l’intérieur des unités du premier degré. Si m_i = M_i, la variance est donnée uniquement par le premier élément. Le second terme représente donc la contribution du sous-échantillonnage.

Nous allons illustrer par un exemple l’analyse d’un échantillon à deux degrés. Le Tableau 5.4 donne des informations sur le poids de l’herbe (toutes espèces mélangées), en kilogrammes, dans des parcelles de 0,025 ha sélectionnées dans 8 compartiments qui ont été choisis au hasard parmi les 40 compartiments d’une étendue forestière. La superficie totale de la forêt était de 1800 hectares.

Tableau 5.4. Poids de l’herbe, en kg, dans des parcelles sélectionnées dans le cadre d’une procédure d’échantillonnage à deux degrés

*Etape 1. Estimer le poids moyen par parcelle de l’herbe, en kg, à l’aide de la formule de l’équation (5.30).

= 1800

étant le nombre total d’unités du second degré, le poids moyen peut être obtenu en divisant la superficie totale (1800 ha) par la taille d’une unité du second degré (0.025 ha).

La moyenne de la population, estimée au moyen de l’équation (5.30), est

= = 105.78

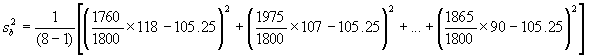
=140.36

La variance de peut être estimée par l’équation (5.32)

=15.4892

= 3.9356

5.6. Echantillonnage à plusieurs phases

L’échantillonnage à plusieurs phases joue un rôle crucial dans les enquêtes forestières, puisqu’il est utilisé aussi bien dans les inventaires forestiers continus que pour estimer le matériel sur pied, ou encore dans les enquêtes par télédétection. L’idée de base de ce mode d’échantillonnage est d’effectuer des sondages distincts, en plusieurs phases successives, commençant par un grand nombre d’unités d’échantillonnage lors de la première phase, et en ne mesurant qu’un sous-ensemble de ces unités durant chaque phase successive, de façon à estimer le paramètre visé avec plus de précision et pour un coût relativement moindre, en étudiant la relation entre les caractères mesurés durant différentes phases. Dans un souci de simplification, nous ne décrirons dans cette section que l’échantillonnage à deux phases, ou échantillonnage double.

Une technique d’échantillonnage qui ne comporte que deux phases (occasions) prend le nom d’échantillonnage à deux phases, ou d‘échantillonnage double. Elle est particulièrement utile dans les situations où l’énumération du caractère étudié (caractère principal) coûte cher ou demande beaucoup de main d’œuvre, alors qu’un caractère auxiliaire corrélé au caractère principal peut facilement être observé. Dans ce cas, il est parfois plus facile et plus économique de prendre un échantillon vaste pour analyser, dans le cadre d’une première phase, la variable auxiliaire. A l’issue de cette phase on obtiendra des estimations précises de la valeur totale ou de la moyenne de la population de la variable auxiliaire. Dans la seconde phase, on choisit un petit échantillon, généralement un sous-échantillon, dans lequel il est possible d’observer à la fois le caractère principal et la variable auxiliaire. A l’aide des renseignements supplémentaires obtenus lors de la première phase, les estimations de régression ou par quotient permettent d’obtenir des estimations précises concernant le caractère principal. La précision des estimations finales peut être accrue en incluant plusieurs variables auxiliaires corrélées, au lieu d’une seule. Par exemple, pour estimer le volume d’un peuplement, les variables auxiliaires peuvent être le diamètre ou la circonférence des arbres et leur hauteur. Pour estimer le rendement en matières tannantes de l’écorce des arbres, on peut choisir comme variables auxiliaires certaines mesures physiques des arbres comme la circonférence, la hauteur, le nombre de pousses etc...

Comme bien d’autres modes d’échantillonnage, l’échantillonnage double est une technique utile pour réduire le coût des énumérations et accroître la précision des estimations. Cette technique peut être très avantageuse dans les enquêtes portant sur des superficies forestières. Elle permet par exemple, après une enquête préliminaire de la forêt en question, d’obtenir une estimation du matériel sur pied à une période ultérieure, par exemple à une distance de 10 à 15 ans, et de sa variation, sur la base d’un échantillon relativement petit.

L’échantillonnage double est également utile pour stratifier une population. Un premier échantillon concernant un caractère auxiliaire peut être utilisé pour subdiviser la population en strates dans lesquelles le deuxième caractère (principal) varie peu. Si les deux caractères sont corrélés, on peut ainsi obtenir des estimations précises du caractère principal, à partir d’un deuxième échantillon relativement petit pour le caractère principal.

Il est possible de conjuguer le double échantillonnage avec d’autres méthodes, comme l’échantillonnage à plusieurs degrés (sous-échantillonnage), qui sont économiques ou qui renforcent la précision des estimations. Par exemple, si l’on veut estimer les disponibilités de graminées, cannes, roseaux etc..., on peut prélever un double échantillon de compartiments (ou parcelles) et de sections t opographiques (ou blocs) pour estimer la surface effective portant les espèces considérées, et un sous-échantillon des sections topographiques, des blocs ou des parcelles pour estimer le rendement.

Dans le cas le plus simple d’un échantillonnage à deux phases, on peut recourir à la technique d’échantillonnage aléatoire simple dans les deux phases. Durant la première étape, la population est divisée en unités d’échantillonnage bien définies et un échantillon est prélevé selon la procédure d’échantillonnage aléatoire simple. Le caractère x est mesuré sur toutes les unités ainsi sélectionnées. Ensuite, on prend un sous-échantillon dans ces unités, sélectionnées à l’aide de la méthode d’échantillonnage aléatoire simple, et on mesure le caractère principal (y) sur ces unités. L’ensemble de la procédure peut également être exécuté en combinaison avec d’autres méthodes, comme la stratification ou l’échantillonnage à plusieurs phases.

Supposons qu’un échantillon de n unités ait été prélevé au hasard, durant la phase initiale, dans la population de N unités, pour observer la variable auxiliaire x, et que l’on prélève un sous-échantillon de taille m au sein duquel on observe à la fois x et le caractère principal.

Soient = moyenne de x dans le premier gros échantillon = (5.35)

= moyenne de x dans le deuxième échantillon = (5.36)

= moyenne de y dans le deuxième échantillon = (5.37)

On peut utiliser pour estimer la moyenne de la population . Toutefois, avec les renseignements précédemment obtenus sur les unités sondées, on peut obtenir une estimation plus précise de en calculant la régression de y en x, et utilisant les informations supplémentaires fournies par le premier échantillon. L’estimation de régression de est donnée par la formule

(5.38)

où le suffixe (drg) dénote l’estimation de régression obtenue grâce au double échantillonnage, et b est le coefficient de régression de y en x, calculé à partir des unités contenues dans le deuxième échantillon de taille m. Ainsi,

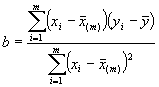(5.39)

La valeur approximative de la variance de l’estimation est donnée par

(5.40)

où (5.41)

(5.42)

L’estimation par quotient s’applique principalement lorsque l’ordonnée à l’origine de la droite de régression de y en x est nulle. L’estimation par le quotient de la moyenne de la population est donnée par la formule

(5.43)

où est l’estimation par quotient, dans l’échantillonnage double. La variance de l’estimation est approximativement donnée par

(5.44)

où

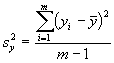(5.45)

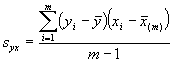(5.46)

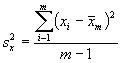(5.47)

(5.48)

Nous allons illustrer par un exemple une analyse de données issues d’un échantillonnage double, avec estimation de régression et estimation par quotient. Le Tableau 5.5 donne des renseignements sur le nombre de cépées et le poids d’herbe correspondant sur des parcelles de 0,025 ha, observés sur un sous-échantillon prélevé au hasard parmi 40 parcelles tirées d’un échantillon préliminaire de 200 parcelles, dans lesquelles seul était compté le nombre de cépées.

Tableau 5.5. Nombre de cépées et poids d’herbe observés sur des parcelles sélectionnées dans le cadre d’une procédure d’échantillonnage à deux phases

Ici, n = 200, m = 40. Le nombre moyen de cépées par parcelle, observé sur l’échantillon préliminaire de 200 parcelles était = 374.4.

, ,

, ,

=

=

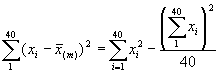
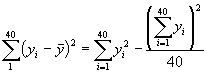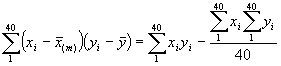Le nombre moyen de cépées par parcelle du sous-échantillon de 40 parcelles est

Poids moyen des cépées par parcelle dans le sous-échantillon de 40 parcelles

L’estimation de régression du poids moyen d’herbe par parcelle (en kg) s’obtient avec l’équation (5.38), où le coefficient de régression b calculé à l’aide de l’équation (5.39) est

b

D’où,

= 52.6 - 0.89

= 51.7 kg /plot

= 82.9

=376.297

La variance approximative de l’estimation est donnée par l’équation (5.40)

(5.40)

= 3.5395

L’estimation par quotient du poids moyen d’herbe par parcelle (en kg) est donnée par l’équation (5.43)

= 51.085

= 3827.708

= 46175.436

= 0.1364

La variance approximative de l’estimation est donnée par l’équation (5.44)

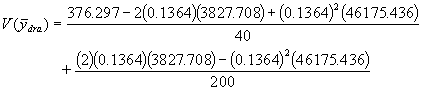
= 5.67

5.7. Echantillonnage avec probabilité proportionnelle à la taille (échantillonnage PPT)

Souvent, les unités d’échantillonnage ont une taille très variable, de sorte qu’un échantillonnage aléatoire simple n’est pas toujours efficace, car il ne tient pas compte de l’importance que peuvent avoir les unités plus grandes de la population. Dans ces situations, on a constaté que les renseignements suppl&e acute;mentaires sur la taille des unités peuvent être mis à profit pour sélectionner l’échantillon de façon à obtenir un estimateur plus précis des paramètres de la population. Une méthode consiste à assigner des probabilités de sélection inégales aux différentes unités de la population. Par exemple, les villages couvrant une zone géographique plus grande ont des chances d’avoir une plus grande superficie sous cultures vivrières. Pour estimer la production, il est donc souhaitable d’adopter un système d’échantillonnage dans lequel la probabilité de sélection des villages est proportionnelle à la zone géographique. Si les unités ont une taille variable et si la variable considérée est directement liée à la taille de l’unité, les probabilités peuvent être assignées proportionnellement à la taille de l’unité. Ce type d’échantillonnage avec probabilité de sélection proportionnelle à la taille de l’unité est appelé "échantillonnage PPT". Lors de la sélection des unités successives de la population, les unités antérieurement sélectionnées peuvent éventuellement être remises dans la population. Dans les paragraphes qui suivent, nous aborderons uniquement l’échantillonnage PPT avec remise des unités d’échantillonnage, car c’est le plus simple des deux systèmes.

La procédure de sélection de l’échantillon consiste à associer à chaque unité un ou des nombre(s) égaux à sa taille et à sélectionner l’unité correspondant à un nombre choisi au hasard dans l’ensemble de nombres associés aux unités. Il existe deux méthodes de sélection que nous allons décrire:

(i) Méthode des totaux cumulés: Supposons que la taille de la i-ème unité soit x_i, (i = 1, 2, …, N). On associe à la première unité les nombres allant de 1 à x_i, à la seconde unité les nombres de (x₁+1) à (x₁+x₂), et ainsi de suite, de manière à ce que le total des nombres ainsi associés soit égal à X = x₁ + x₂ + … + x_N. Ensuite, on choisit au hasard un nombre aléatoire de 1 à X et on sélectionne l’unité associée à ce nombre.

Par exemple, un village a 8 vergers contenant respectivement 50, 30, 25, 40, 26, 44, 20 et 35 arbres. Un échantillon de 3 vergers doit être sélectionné avec remise et avec probabilité proportionnelle au nombre d’arbres dans les vergers. La table des totaux cumulés se présentera comme suit:

Enfin, on choisit trois nombres aléatoires entre 1 et 270: ces nombres sont 200, 116 et 47. Les unités associées à ces nombres sont la 6^ème, la 4^ème, et la 1^ère. L’échantillon ainsi sélectionné contient donc les unités portant les numéros de série 1, 4 et 6.

ii) Méthode de Lahiri: Comme on l’a vu, avec la méthode des totaux cumulés, il faut reporter les totaux cumulés successifs, ce qui est à la fois long et fastidieux, en particulier si les populations sont importantes. En 1951, Lahiri a proposé une autre procédure qui évite cette opération. La méthode de Lahiri consiste à sélectionner un couple (i,j) de nombres aléatoires, où 1 £ i £ N et 1£ j £ M; la lettre M désignant le maximum des tailles des N unités de la population. Si j £ X_i, on sélectionne la i-ème unité. Dans le cas contraire, la paire de nombres aléatoires est rejetée et on choisit une autre paire. Pour sélectionner un échantillon de n unités, la procédure doit être répétée jusqu’à ce que les n unités soient choisies. Cette procédure permet de déterminer les probabilités de sélection requises.

Par exemple, pour sélectionner, par la méthode de Lahiri de sélection d’un PPT avec remise, un échantillon de 3 vergers dans la population de l’exemple précèdent (N = 8, M = 50 et n = 3), on sélectionne trois paires de nombres aléatoires, dont le premier élément est inférieur ou égal à 8 et le second inférieur ou égal à 50. Les trois paires sélectionnées dams la table des nombres aléatoires sont (2, 23) (7,8) et (3, 30). Etant donné que, dans la troisième paire, j >X_i, une nouvelle paire doit être sélectionnée. Celle-ci est (2, 18). L’échantillon sélectionné selon cette procédure est donc constitué des unités portant les numéros de série 2, 7 et 2. Comme l’unité 2 revient deux fois dans l’échantillon, la taille de l’échantillon est 2, dans ce cas. Pour obtenir une taille de l’échantillon de trois, on peut répéter la procédure d’échantillonnage pour obtenir une nouvelle unité (distincte).

Supposons qu’un échantillon de n unités soit tiré d’une population de N unités, par la technique d’échantillonnage PPT avec remise. De plus, désignons par (y_i, p_i) la valeur et la probabilité de sélection de la i-ème unité de l’échantillon, i = 1, 2, 3, …., n.

On obtient un estimateur non biaisé de la moyenne de la population par la formule

(5.49)

Un estimateur de la variance de cet estimateur est donné par

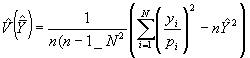(5.50)

où ,

Nous allons illustrer ceci par un exemple. Un échantillon aléatoire de 23 unités sur 69 a été sélectionné avec probabilité proportionnelle à la taille de l’unité (compartiment) dans une superficie forestière dans UP. La surface totale des 69 unités était de 14079 ha. Les volumes de bois déterminés pour chaque compartiment sélectionné sont données dans le Tableau 5.6, avec la superficie du compartiment.

Tableau 5. 6. Volume de bois et taille de l’unité d’échantillonnage pour un échantillon PPT de compartiments forestiers.

Superficie totale X = 14079 ha.

On obtient un estimateur non biaisé de la moyenne de la population par l’équation (5.49).

= 1073.312

Et une estimation de la variance de à l’aide de l’équation (5.50).

= 17514.6

Et l’erreur-type de est = 132.343.