Os exercícios são numerados de acordo com os números das secções relevantes do manual.
Exercício 2.1 Valor médio e variância
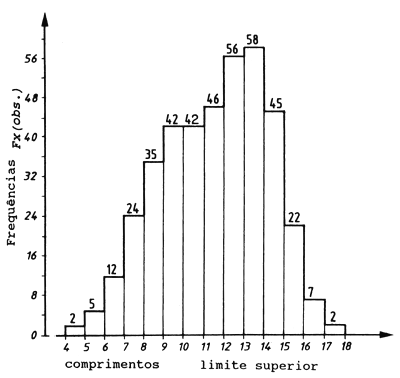
Neste exercício, usa-se parte dos dados da distribuição de frequências da truta coral (Plectropomus leopardus) apresentados na Fig. 3.4.0.2. As frequências de comprimento usadas para este exercício estão na Fig. 17.2.1. Somente os dados do intervalo de comprimento 23–29 cm são usados e assumidos como pertencendo a uma coorte.
Tarefas:
Ler as frequências, F(j) da Fig. 17.2.1 e completar a folha de exercícios. Calcular a média, a variância e o desvio padrão.
Folha de exercícios 2.1
| j | L(j)-L(j) +dL | F(j) | L(j) | F(j) *L(j) | L(j) -x | F(j) *(L(j)-x)2 |
| 1 | - | -2.968 | ||||
| 2 | - | -2.468 | ||||
| 3 | - | -1.968 | ||||
| 4 | - | -1.468 | ||||
| 5 | - | -0.968 | ||||
| 6 | - | -0.468 | ||||
| 7 | - | 0.032 | ||||
| 8 | 26.5–27.0 | 6 | 26.75 | 160.50 | 0.532 | 1.698 |
| 9 | 27.0–27.5 | 2 | 54.50 | 1.032 | 2.130 | |
| 10 | 27.5–28.0 | 2 | 55.50 | 1.532 | 4.694 | |
| 11 | 28.0–28.5 | 2 | 56.50 | 2.032 | 8.258 | |
| 12 | 28.5–29.0 | 1 | 28.75 | 2.532 | 6.411 | |
| somas | ∑F(j) 31 | ∑F(j) *L(j) | ∑F(j) *(L(j) -x)2 | |||
| x = | s2 = | s = | ||||
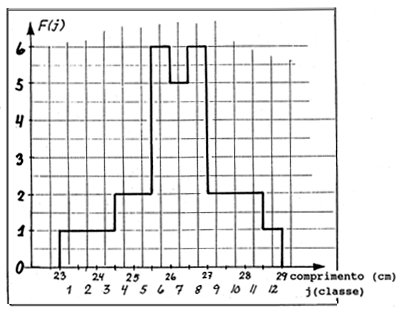
Fig. 17.2.1 Amostra de frequências de comprimento
Exercício 2.2 Distribuição normal
Este exercício consiste em ajustar uma distribuição normal à amostra de frequências de comprimento do Exercício 2.1 aplicando a expressão:
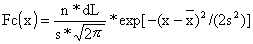 | (Eq. 2.2.1) |
para um número suficiente de valores de x que permitam traçar a curva em forma de sino.
Para sua maior conveniência, introduzir os símbolos auxiliares:
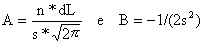
de modo que a fórmula acima possa ser escrita
Fc(x) = A*exp(B*(x-x)2)
Como A e B não dependem de L, e como vamos usá-los várias vezes, é conveniente calculá-los separadamente.
Tarefas:
1) Calcular A e B
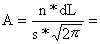
B = -1/(2s2) =
2) Calcular Fc(x) para os seguintes valores de x:
Folha de exercícios 2.2
| x | Fc(x) | x | Fc(x) |
| 22.0 | 26.0 | ||
| 22.5 | 26.5 | ||
| 23.0 | 27.0 | ||
| 23.5 | 27.5 | ||
| 24.0 | 28.0 | ||
| 24.5 | 28.5 | ||
| 25.0 | 29.0 | ||
| 25.5 | 29.5 |
3) Traçar a curva em forma de sino na Fig. 17.2.1
Exercício 2.3 Limites de confiança
Tarefas:
Calcular, o intervalo de confiança ao nível de 95%, para o valor médio estimado no Exercício 2.1.
Exercício 2.4 Análise de regressão linear simples
É comum observar-se que, quanto maior for o número de barcos que participa numa pescaria, menor será a captura por barco. Isso não é de admirar, quando se considera o manancial pesqueiro como um recurso limitado que tem que ser repartido entre todos os barcos. No Capítulo 9 tratamos da teoria pesqueira que sustenta esse modelo.
Os dados na folha de exercícios abaixo são da pesca de camarões do pasquistão (Van Zalinge e Sparre, 1986).
Tarefas:
Folha de exercícios 2.4
| ano | i | número de barcos x(i) | x(i)2 | captura por barco/ano y(i) | y(i)2 | x(i) *y(i) |
| 1971 | 1 | 456 | 43.5 | 19836.0 | ||
| 1972 | 2 | 536 | 44.6 | 23905.6 | ||
| 1973 | 3 | 554 | 38.4 | 21273.6 | ||
| 1974 | 4 | 675 | 23.8 | 16065.0 | ||
| 1975 | 5 | 702 | 25.2 | 17690.4 | ||
| 1976 | 6 | 730 | 532900 | 30.5 | 930.25 | |
| 1977 | 7 | 750 | 562500 | 27.4 | 750.76 | |
| 1978 | 8 | 918 | 842724 | 21.1 | 445.21 | |
| 1979 | 9 | 928 | 861184 | 26.1 | 681.21 | |
| 1980 | 10 | 897 | 804609 | 28.9 | 835.21 | |
| Total | 7146 | 309.5 | 211099.5 | |||
| x = | y = | |||||
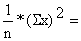 | 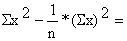 | |||||
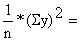 | 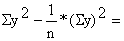 | |||||
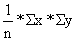 | ||||||
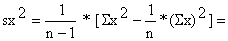 | sx = | |||||
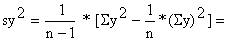 | sy = | |||||
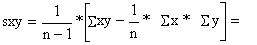 | ||||||
| declive: | 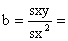 | intersecção: a = y-b*x= | ||||
variância de b: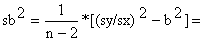 | sb = | |||||
variância de b: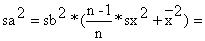 | sa = | |||||
| distribuição de Student: t(n-2) = | ||||||
| limites de confiança: b-sb*tn-2, b+sb*tn-2 = [ , ] a-sa*tn-2, a+sa*tn-2 = [ , ] | ||||||
Exercício 2.5 Coeficiente de correlação
No Exercício 2.4, faz sentido o coeficiente de correlação da regressão das capturas por barco contra o número de barcos? Avaliar qual das duas variáveis é considerada naturalmente a variável independente. Podemos (em princípio) decidir antecipadamente os valores de uma delas?
Tarefas:
Independentemente da escolha na primeira parte do exercício calcular os limites de confiança do r ao nível de 95%.
Exercício 2.6 Transformações normais, utilizadas como um instrumento para separar duas distribuições normais sobrepostas (método de Bhattacharya).
A Fig. 17.2.6A mostra a distribuição de frequências resultante de duas distribuições normais sobrepostas “a” e “b”. Assumimos que as frequências apresentadas na Fig. 17.2.6B também são uma combinação de duas distribuições normais. O exercício visa separar estas duas componentes. O tamanho total da amostra é 398. Assumir que cada componente tem 50% do total, ou seja 199. Assumir ainda que as frequências do lado esquerdo da distribuição são inteiramente representativas da componente “a”, enquanto que as do lado direito são inteiramente representativas da componente “b”.
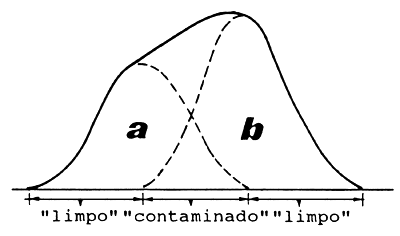 |  |
| Fig. 17.2.6A Distribuição combinada de duas distribuições normais sobrepostas | Fig. 17.2.6B Amostra de frequências de comprimento (assume-se que consta de duas distribuições normais) |
Tarefas:
Completar a folha de exercícios 2.6a.
Graficar Δln F(z) = y' contra x + dL/2 = z e decidir quais os pontos que estão em linhas rectas com declives negativos (ver Fig. 2.6.5).
Com base na opção anterior escolher os pontos a utilizar para as regressões lineares. (Evitar áreas sobrepostas e pontos baseados em muito poucas observações). Fazer as duas regressões lineares e determinar a e b.
Calcular x = -a/b, s2 = -1/b e √ s2 para cada componente.
Traçar as duas rectas que representam cada distribuição em forma linear.
Queremos agora converter as linhas rectas nas correspondentes distribuições (calculadas) teóricas normais. Usando a Eq. 2.2.1, calcular Fc(x) de ambas as distribuições normais para um número suficiente de valores de x permitindo-lhe traçar as duas curvas em forma de sino sobrepostas na Fig. 17.2.6B. Assumir n = 199 para ambas as componentes (utilizar o mesmo método apresentado no Exercício 2.2) e completar a folha de exercícios 2.6B.
Folha de exercícios 2.6a
| intervalo | x | F(x) | ln F(x) | Δln F(z) | z = x+dL/2 |
| 4– 5 | 4.5 | 2 | 0.693 | ||
| 0.916 | 5 | ||||
| 5– 6 | 5.5 | 5 | 1.609 | ||
| 0.875 | 6 | ||||
| 6– 7 | 6.5 | 12 | |||
| 7 | |||||
| 7– 8 | 7.5 | 24 | |||
| 8– 9 | 8.5 | 35 | |||
| 9–10 | 9.5 | 42 | |||
| 10–11 | 10.5 | 42 | |||
| 11–12 | 11.5 | 46 | |||
| 12–13 | 12.5 | 56 | |||
| 13–14 | 13.5 | 58 | |||
| 14–15 | 14.5 | 45 | |||
| 15–16 | 15.5 | 22 | 3.091 | ||
| -1.145 | 16 | ||||
| 16–17 | 16.5 | 7 | 1.946 | ||
| -1.253 | 17 | ||||
| 17–18 | 17.5 | 2 | 0.693 | ||
Folha de exercícios 2.6b
| Primeira componente | Segunda componente |
| A = | A = |
| B = | B = |
| x = | x = |
Fc(x) = A*exp[B*(x-x)2]
| x | Fc(x) primeira | Fc(x) segunda |
| 1.5 | ||
| 2.5 | ||
| 3.5 | ||
| 4.5 | ||
| 5.5 | ||
| 6.5 | ||
| 7.5 | ||
| 8.5 | ||
| 9.5 | ||
| 10.5 | ||
| 11.5 | ||
| 12.5 | ||
| 13.5 | ||
| 14.5 | ||
| 15.5 | ||
| 16.5 | ||
| 17.5 | ||
| 18.5 | ||
| 19.5 | ||
| 20.5 |
Exercício 3.1 Equação de crescimento de von Bertalanffy
Os seguintes parâmetros de crescimento do luciano (Lutjanus malabaricus) do Mar de Arafura foram reportados por Edwards (1985):
K = 0.168 por ano
L∞ = 70.7 cm (comprimento padrão)
to = 0.418 ano
Edwards também estimou a relação peso/comprimento padrão para Lutjanus malabaricus:
W = 0.041*L2.842 (peso em g e comprimento padrão em cm)
bem como a relação comprimento padrão (S.L.) e comprimento total (T.L.):
T.L. = 0.21+1.18*S.L.
Tarefas:
Completar a folha de exercícios e traçar as três curvas seguintes:
Folha de exercícios 3.1
| idade | compr. padrão | comprim. total | peso do corpo |
| anos | cm | cm | g |
| 0.5 | |||
| 1.0 | |||
| 1.5 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 | |||
| 12 | |||
| 14 | |||
| 16 | |||
| (não usar idades superior a 16 no gráfico) | |||
| 20 | |||
| 50 | |||
Exercício 3.1.2 Equação de crescimento de von Bertalanffy baseada em pesos
Pauly (1980) determinou os seguintes parâmetros para o peixe-pónei (Leiognathus splendens) da Indonesia:
L∞ = 14 cm
q = 0.02332
K = 1.0 por ano
to = -0.2 ano
Tarefas:
Completar a folha de exercícios e traçar o comprimento e o peso convertidos das curvas de crescimento de von Bertalanffy.
Folha de exercícios 3.1.2
| idade t | comprimento L(t) | peso W(t) |
| 0 | ||
| 0.1 | ||
| 0.2 | ||
| 0.3 | ||
| 0.4 | ||
| 0.5 | ||
| 0.6 | ||
| 0.7 | ||
| 0.8 | ||
| 0.9 | ||
| 1.0 | ||
| 1.2 | ||
| 1.4 | ||
| 1.6 | ||
| 1.8 | ||
| 2.0 | ||
| 2.5 | ||
| 3.0 |
Exercício 3.2.1 Dados de leitura de idades e composição por comprimentos (chave idade/comprimento)
Considerar a Tabela 3.2.1.1 (chave idade/comprimento) e supor que capturámos um total de 2400 peixes da espécie em questão, durante o cruzeiro no qual esta chave idade/comprimento foi obtida, e que somente 439 indivíduos da Tabela 3.2.1.1 foram amostrados para a idade. Do restante foi medido o comprimento total. Para reduzir o trabalho de processamento dos dados, utilizou-se somente uma parte da amostra (386 peixes) desta distribuição de frequências de comprimentos que é mostrada na folha de exercícios.
Tarefas:
Estimar quantos destes 386 peixes pertenciam a cada uma das seis coortes listadas na Tabela 3.2.1.1, completando a folha de exercícios.
Folha de exercícios 3.2.1
| coorte | 1982 p | 1981 o | 1981 p | 1980 o | número na amostra de comprim. | 1982 p | 1981 o | 1981 p | 1980 o |
| intervalo de compr. | chave | números por coorte | |||||||
| 35–36 | 0.800 | 0.200 | 0 | 0 | 53 | 42.4 | 10.6 | 0 | 0 |
| 36–37 | 0.636 | 0.273 | 0.091 | 0 | 61 | 38.8 | 16.7 | 5.6 | 0 |
| 37–38 | 49 | ||||||||
| 38–39 | 52 | ||||||||
| 39–40 | 70 | ||||||||
| 40–41 | 52 | ||||||||
| 41–42 | 0.222 | 0.444 | 0.222 | 0.111 | 49 | 10.9 | 21.8 | 10.9 | 5.4 |
| total | 386 | 187.2 | 133.8 | ||||||
Exercício 3.3.1 Diagrama de Gulland e Holt
Randall (1962) fez a marcação e recaptura de peixes-cirurgião (Acanthurus bahianus) próximo às Ilhas Virgens. Dados de 11 dos peixes recapturados são mostrados na folha de exercícios. Os comprimentos ao libertarem os peixes estão na coluna B; os comprimentos na recaptura, na coluna C e o tempo decorrido entre a libertação e a recaptura está na coluna D.
Tarefas:
Estimar K e L∞ do peixe-cirurgião (Acanthurus bahianus) usando o diagrama de Gulland e Holt.
Calcular os limites de confiança de K, ao nível de 95%.
Folha de exercícios 3.3.1
| A | B | C | D | E | F |
| número do peixe | L(t) cm | L(t+Δt) cm | Δt dias | 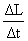 cm/ano (y) | 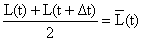 cm (x) |
| 1 | 9.7 | 10.2 | 53 | ||
| 2 | 10.5 | 10.9 | 33 | ||
| 3 | 10.9 | 11.8 | 108 | ||
| 4 | 11.1 | 12.0 | 102 | ||
| 5 | 12.4 | 15.5 | 272 | ||
| 6 | 12.8 | 13.6 | 48 | ||
| 7 | 14.0 | 14.3 | 53 | ||
| 8 | 16.1 | 16.4 | 73 | ||
| 9 | 16.3 | 16.5 | 63 | ||
| 10 | 17.0 | 17.2 | 106 | ||
| 11 | 17.7 | 18.0 | 111 |
| a (intersecção) = | b (declive) = |
| K = | L∞ = |
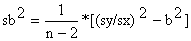 = = | |
| sb = | t(n-2) = |
| intervalo de confiança K = |
Exercício 3.3.2 Diagrama de Ford-Walford e o método de Chapman
Postel (1955) apresentou a seguinte relação peso/comprimento para o albacora (Thunnus albacares) da Costa do Senegal:
| idade | (anos) | comprimento furcal (cm) |
| 1 | 35 | |
| 2 | 55 | |
| 3 | 75 | |
| 4 | 90 | |
| 5 | 105 | |
| 6 | 115 |
Tarefas:
Estimar K e L∞ usando o diagrama de Ford-Walford e o método de Chapman.
Folha de exercícios 3.3.2
| Marcar no grafico | FORD-WALFORD | CHAPMAN | |
| t | L(t+Δt) (y) | L(t) (x) | L(t+Δt)-L(t) (y) |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| a (intersecção) | |||
| b (declive) | |||
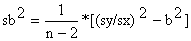 | |||
| tn-2 limite de confiança de b | |||
| K | |||
| L∞ |
Exercício 3.3.3 Diagrama de von Bertalanffy
Cassie (1954) apresentou uma amostra de distribuição de frequências de 256 douradas australianas (Chrysophrys auratus) conforme a figura abaixo. o autor decompôs esta amostra em componentes com uma distribuição normal (semelhante à Fig. 3.2.2.2) usando o método de Cassie (cf. Secção 3.4.3), e encontrou os seguintes comprimentos médios para quatro grupos de idade (cf. Fig. 17.3.3.3):
| A | B | C | D |
| grupo de idade | comp. médio (pol.) | ΔL/Δt | L |
| 0 | 3.22 | ||
| 2.11 | 4.28 | ||
| 1 | 5.33 | ||
| 2.29 | 6.48 | ||
| 2 | 7.62 | ||
| 2.12 | 8.68 | ||
| 3 | 9.74 |
Nota: Num diagrama de Gulland e Holt resulta (cf Colunas C e D): K = -0.002 e L∞ = -950 polegadas, o que não faz qualquer sentido.
Tarefas:
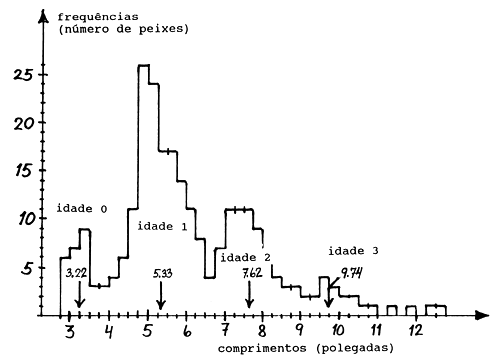
Fig. 17.3.3.3 Distribuição de frequências de comprimento de 256 douradas australianas. As setas indicam comprimentos médio por grupos de idade determinado por Cassie (1954)
Exercício 3.4.1 Método de Bhattacharya
Weber e Jothy (1977) apresentaram a amostra de distribuição de frequências de comprimento de 1069 falsos-besugos (Nemipterus nematophorus) mostrada na Fig. 17.3.4.1A. Estes peixes foram capturados durante um cruzeiro realizado entre 29 de Março a 1 de Maio de 1972, no mar do Sul da China ao longo da costa de Sarawak. As medidas tomadas são do comprimento total, do focinho à extremidade do lóbulo inferior da barbatana caudal.
As Figs. 17.3.4.1B e 17.3.4.1C mostram o diagrama de Bhattacharya para os dados da Fig. 17.3.4.1A, onde B é baseado nos dados originais com intervalos de comprimento de 5 mm e C nos mesmos dados reagrupados em intervalos de 1 cm. Deve-se utilizar a Fig. C por duas razões: 1) parece ser mais fácil visualisar uma estrutura na Fig. C do que visualisar na Fig. B, e 2) porque o número de cálculos é menor.
Tarefas:
Decompor a amostra de frequências de comprimentos (classes de 1 cm, Fig. C) em componentes normalmente distribuídos e estimar, a partir daí, o comprimento médio e o desvio padrão para cada componente. Usar as quatro folhas de exercícios e traçar as rectas de regressão.
Estimar L∞ e K usando o diagrama de Gulland e Holt. Traçar o gráfico.
Pensar se a análise poderia obter melhores resultados usando a Fig. B (classes de comprimento de 5 mm) em vez da Fig. C (classes de 1 cm)?
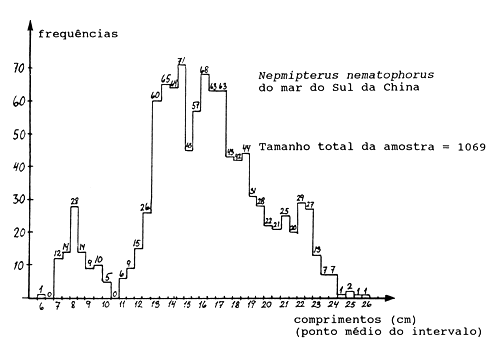
Fig. 17.3.4.1A Amostra da frequências de comprimentos dos falsos-besugos. Fonte de dados: Weber e Jothy, 1977
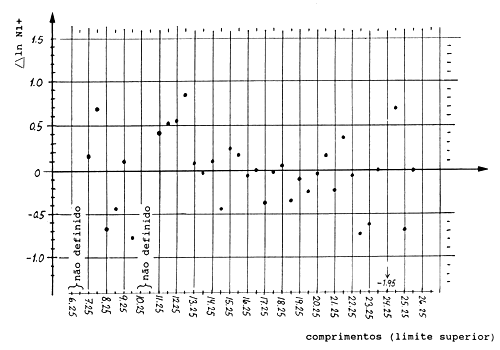
Fig. 17.3.4.1B Diagrama de Bhattacharya dos dados da Fig. 17.3.4.1A baseada nos dados originais, intervalo de comprimento 5 mm
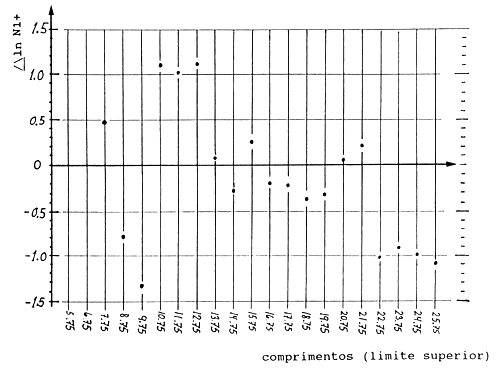
Fig. 17.3.4.1C Diagrama de Bhattacharya dos dados da Fig. 17.3.4.1A baseada nos dados reagrupados em intervalos de comprimento de 1 cm (utilizados no exercício)
Folha de exercícios 3.4.1a
| A | B | C | D | E | F | G | H | I |
| intervalo de comprimento | N1+ | ln N1+ | Δln N1+ | L | Δln N1 | ln N1 | N1 | N2+ |
| (cm) | (y) | (x) | ||||||
| 5.75– 6.75 | 1 | 0 | - | - | - | - | 1 | 0 |
| 6.75– 7.75 | 26 | 3.258 | (3.258) | 6.75 | 1.262 | - | 26 | 0 |
| 7.75– 8.75 | 42# | 3.738# | 0.480 | 7.75 | 0.354 | 3.738# | 42# | 0 |
| 8.75– 9.75 | 19 | 2.944 | -0.793 | 8.75 | -0.554 | 3.183 | 19 | 0 |
| 9.75–10.75 | 5 | 9.75 | ||||||
| 10.75–11.75 | 15 | 10.75 | ||||||
| 11.75–12.75 | 41 | 11.75 | ||||||
| 12.75–13.75 | 125 | 12.75 | ||||||
| 13.75–14.75 | 135 | 13.75 | ||||||
| 14.75–15.75 | 102 | 14.75 | ||||||
| 15.75–16.75 | 131 | 15.75 | ||||||
| 16.75–17.75 | 106 | 16.75 | ||||||
| 17.75–18.75 | 86 | 17.75 | ||||||
| 18.75–19.75 | 59 | 18.75 | ||||||
| 19.75–20.75 | 43 | 19.75 | ||||||
| 20.75–21.75 | 45 | 20.75 | ||||||
| 21.75–22.75 | 56 | 21.75 | ||||||
| 22.75–23.75 | 20 | 22.75 | ||||||
| 23.75–24.75 | 8 | 23.75 | ||||||
| 24.75–25.75 | 3 | 24.75 | ||||||
| 25.75–26.75 | 1 | 25.75 | ||||||
| Total | 1069 |
| a (intersecção) = | b (declive) = |
| L(N1) = -a/b = | 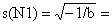 |
Folha de exercícios 3.4.1b
| A | B | C | D | E | F | G | H | I |
| intervalo | N2+ | ln N2+ | Δln N2+ | L | Δln N2 | ln N2 | N2 | N3+ |
| 5.75– 6.75 | ||||||||
| 6.75– 7.75 | 6.75 | |||||||
| 7.75– 8.75 | 7.75 | |||||||
| 8.75– 9.75 | 8.75 | |||||||
| 9.75–10.75 | 9.75 | |||||||
| 10.75–11.75 | 10.75 | |||||||
| 11.75–12.75 | 11.75 | |||||||
| 12.75–13.75 | 12.75 | |||||||
| 13.75–14.75 | 13.75 | |||||||
| 14.75–15.75 | 14.75 | |||||||
| 15.75–16.75 | 15.75 | |||||||
| 16.75–17.75 | 16.75 | |||||||
| 17.75–18.75 | 17.75 | |||||||
| 18.75–19.75 | 18.75 | |||||||
| 19.75–20.75 | 19.75 | |||||||
| 20.75–21.75 | 20.75 | |||||||
| 21.75–22.75 | 21.75 | |||||||
| 22.75–23.75 | 22.75 | |||||||
| 23.75–24.75 | 23.75 | |||||||
| 24.75–25.75 | 24.75 | |||||||
| 25.75–26.75 | 25.75 | |||||||
| Total |
| a (intersecção) = | b (declive) = |
| L(N2) = -a/b = | 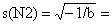 |