1. Components of effective rainfall and their measurement
2. Empirical methods of determining effective rainfall
3. Determining effective rainfall from formula
4. Evaluation of methods
The evaluation of effective rainfall involves measuring rainfall and/or irrigation, losses toy surface run-off, percolation losses beyond the root zone and the soil moisture uptake by the crop for evapotranspiration. Information is needed on rooting depth of crop plants. Components are measured directly or indirectly and either individually or in an integrated way.
Total rainfall can be measured directly with rain gauges. Several types of recording and non-recording gauges are available. The instruments and their use have been described by WMO (1970). Irrigation applications can be measured with various types of notches, weirs, Parshall flumes, out-throat flumes and with direct recording water meters. The methods have been compiled and described by Dastane (1972),
With efficient farm water management, surface run-off should be kept to a minimum. Only excess water should be removed by deep percolation and sub-surface drainage or by surface drainage. For a given field, run-off can be assessed with measuring flumes and water stage recorders or can be computed with formulae established for different conditions, as given in the Handbook on Hydrology by Chow (1964), and USDA Field Manual for Research in Agricultural Hydrology (1968).
For determining the water losses due to deep percolation and water uptake by a crop, the depth of rooting must first be known. The depth of root system varies from crop to crop and also from time to time during growth. The root system is influenced by several factors; too much wetness results in development of a shallow root system while drier soil water regimes encourage a deep one; soil texture and structure influence the depth of the root system to a great extent. Studies on rooting depths should, therefore, be made under existing and recommended cultural and irrigation practices on representative soils. The two most common methods of measuring the rooting depth are by excavation method and by studying soil moisture extraction patterns.
With the excavation method the roots are carefully dug from the soil, then cleaned, dried and weighed. The length and distribution in different layers is noted. The process is simple but laborious and careful handling is needed. But what is the effective root depth; is it the longest root or the mean root length? As a first approximation, the soil depth in which 90 percent (by weight) of the roots lie, can be taken as the effective root zone for irrigation purposes. However, several investigators have pointed out that the mass of roots and their activity do not have a simple linear relationship. There are generally more roots in the surface layer. Also, sometimes water extraction can be greater from the sub-soil than the surface soil. Water is extracted from a layer where it is readily available, provided there is a certain minimum root permeation in that layer. Soil moisture depletion can be determined by periodical soil sampling or by means of devices such as gypsum blocks or neutron probes. For irrigation purposes, the soil depth over which 80 percent of the total water intake takes place can toe regarded as the effective root zone of a crop. Since the root system is dynamic and continues to extend up to the flowering time, such studies are necessary at monthly or fortnightly intervals.
Deep percolation losses can toe determined directly by using lysimeters or indirectly by computation of soil characteristics including soil water content, soil moisture tension and soil permeability. With the direct method, a representative and undisturbed soil column is enclosed in a large container or a tank fitted with an outlet at the bottom from which excess water can be drained into a measuring cylinder; this is the so-called drainage lysimeter. The lysimeter needs to be surrounded by a large cropped area. The method has been widely used since all the components of water gains and water losses can be measured from which a water balance can be obtained. For details, reference is made to comprehensive studies by Anonymous (1967), Harrold (1968), Hillel et al (1969), Rose et al (1966), and McGuinness and Bordne (1972).
For the indirect method, the moisture holding capacity of the soil is calculated layer by layer from the field capacity, wilting point, bulk density, soil depth and rooting depth. Any excess over the water holding capacity of the soil will normally be a deep percolation loss. The values of the first four parameters can be determined using established methodologies (Dastane, 1972).
With a dry subsoil deep percolation losses take place under saturated soil conditions but will continue even after field capacity has been reached. In the Great Plains of the U.S.A., the soil water storage efficiency is sometimes lower than 20 percent on fallow lands left for water harvesting. Accurate measurement of the deep percolation component under both saturated and unsaturated soil conditions is rather laborious. Rooting depth and root concentration must be known. A method has been described by Hillel et al (1972).
The level of evapotranspiration is controlled mainly by three factors, namely, plant characteristics, extent of ground cover and stage of growth; water availability in the soil; and meteorological parameters or the evaporative demand. Maximum or potential evapotranspiration (ETp) occurs when the soil water is non-limiting and the crop is in an active stage of growth with full ground cover; the level of ETp for a given plant species is then mainly governed by the meteorological conditions.
Actual evapotranspiration (ETa), which is also sometimes called consumptive water use, is the actual quantity of water lost during crop growth by evaporation from land surface and by transpiration by plants.
The ETa may reach ETp level if conditions permit. It is more difficult to estimate ETa than ETp since several factors play interacting roles. The ETa can be determined directly by periodic soil sampling and oven-drying; changes in soil water by the growing crop are followed and layerwise depletions are studied in the effective root zone of the crop. It is a very laborious method and is subject to sampling errors.
The ETp can be computed from the meteorological parameters such as temperature, radiation, wind velocity, humidity. Several different formulae to compute ETp are available. Some formulae in computing ETp and also ETa are listed in Table 3 along with the parameters considered. None of the formulae suits all situations perfectly. Some improved methods need elaborate sets of meteorological data which are not always available. Prohibitive costs of installation and operation of equipment, time involved in processing the data and the variety of crops grown make it impossible to use and apply these formulae in day to day agricultural operations.
A simple method such as measurement of open pan evaporation has been proposed since it represents the effect of all meteorological elements in an integrated way. Since only one parameter is to be measured, it is relatively easy to use this technique in the field. The relationship between open pan evaporation and ETp however, is intricate. Local coefficients relating pan evaporation to ETp should preferably be established locally. The value of potential evapotranspiration where there is a non-limiting water supply varies from 0.4 to 0.8 times the U.S, Class A Open Pan Evaporimeter under different conditions of pan specifications and its method of installation. It offers a good approximation for practical purposes. For details, refer to FAO Irrigation and Drainage paper no. 24 (1974).
Table 3: FORMULAE TO PREDICT CROP EVAPOTRANSPIRATION
|
|
Variables considered (+) |
|
|||||||||||||
|
Formula by |
Temperature |
Air humidity |
Dry-wet bulb temp |
Drylight hours |
Sunshine hours/cloud cover |
Radiation |
Wind velocity |
Evaporimeter |
Crop data |
Crop factor |
Soil factor |
Correction factor |
Precipitation |
Barograph |
Entity measured |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Rohwer, 1931, USA |
+ |
+ |
|
|
|
|
+ |
|
|
|
+ |
|
|
+ |
ET crop |
|
Blaney-Morin, 1942, USA |
+ |
+ |
|
+ |
|
|
|
|
|
+ |
|
|
|
|
ET crop |
|
Lowry-Johnson, 1942, USA |
+ |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
ET of valley, entire growing season |
|
Thornthwaite, 1943, USA |
+ |
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
ET crop, adequate |
|
Penman, 1948, UK |
+ |
+ |
|
+ |
+ |
+ |
+ |
|
|
+ |
|
|
|
|
Eo or ET crop |
|
Blaney-Criddle, 1950, USA |
+ |
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
Cu crop |
|
Halstead, 1951, USA |
+ |
+ |
+ |
+ |
|
|
|
|
|
|
|
|
|
|
ET crop |
|
Haude, 1952, Germany |
|
|
+ |
+ |
|
|
+ |
|
|
|
|
+ |
|
|
ET crop |
|
Turo, 1954, France |
+ |
+ |
|
+ |
+ |
+ |
+ |
|
|
|
|
|
|
|
ET crop |
|
Turo-Langbein, 1954, |
+ |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
Eo or ET crop, |
|
France |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
annual river basin |
|
Halkais. 1955, USA |
|
|
|
|
|
|
|
+ |
|
|
|
+ |
|
|
CU crop |
|
Thornthwaite-Mather, 1955 |
+ |
|
|
|
+ |
|
|
|
|
|
+ |
+ |
+ |
|
ET crop and soil |
|
USA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
water balance |
|
van Bavel, 1956, USA |
+ |
|
|
+ |
+ |
+ |
|
|
|
|
|
+ |
|
|
ET crop |
|
Hargreaves, 1956, USA |
+ |
+ |
|
+ |
|
|
|
|
|
+ |
|
|
|
|
Eo or ET crop |
|
Ivanov, 1957, USSR |
+ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
ET crop under adequate moisture |
|
Makkink, 1957, Holland |
+ |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
ET grass |
|
Rijtoma, 1957. Holland |
+ |
+ |
|
+ |
+ |
+ |
+ |
|
+ |
|
|
|
|
|
ET crop |
|
McIlroy, 1961, Australia |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
|
+ |
|
|
|
|
ET crop |
|
Olivier, 1961. UK |
+ |
+ |
+ |
|
+ |
+ |
|
|
|
|
+ |
|
+ |
|
Basic water needs for crop/land unit |
|
Jensen-Haise, 1963, USA |
+ |
|
|
+ |
+ |
+ |
|
|
|
+ |
|
+ |
|
|
ET crop |
|
Christianson, 1966, USA |
+ |
+ |
|
|
+ |
+ |
+ |
|
|
|
|
+ |
|
|
Eo |
|
Dastane, 1967, India |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
ET crop |
|
Linacro, 1967, Australia |
+ |
+ |
|
+ |
+ |
+ |
+ |
|
+ |
|
|
|
|
|
ET crop |
ET = Evapotranspiration
CU = Consumptive use of water
Eo = Evaporation from U.S. Class A avaporimeter placed in a grass field.
In deriving relationship between ETa and soil water content, four main approaches can be distinguished, as shown in Fig 2:
Fig 2: RELATION BETWEEN ACTUAL TO POTENTIAL EVAPOTRANSPIRATION AND SOIL MOISTURE CONTENT
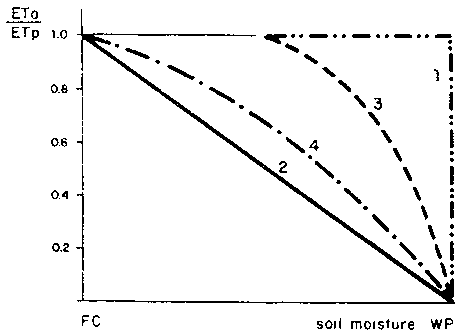
1 a constant ET and sudden reduction at wilting point (WP);
2 a decreasing linear rate of ET with decrease in soil water content;
3 a linear cum exponential decreasing rate of ET with decrease in soil water content;
4 an exponential decreasing rate of ET with decrease in soil water content.
Each of the four curves given in Fig 2 is possible under a given situation. Considerable literature has accumulated on the subject during the last two decades. Reference is made to Slatyer and McIlroy (1961), Linacre (1963), Konstantinov (1963), Hagan et al (1967) and Gangopadhyaya et al (1968),
2.1 Soil Moisture Changes
2.2 Daily Soil Moisture Balance Method
2.3 Integrating Gauge
2.4 The Ramdas Method
2.5 Lysimeters
2.6 Drum Technique for Rice
There are several methods of assessing effective rainfall. Each method has certain merits and limitations.
Water in the root zone may be measured by sampling and oven-drying the soil before and after every shower of rain. The increase in soil moisture, plus evapotranspiration loss (ETa) from the time the rain starts until the soil is sampled, is the amount of effective rainfall. After heavy rainfall evapotranspiration can be assumed to be at the potential rate during the short period from cessation of rainfall until the sampling time. This can be taken as 0.4 to 0.8 times the evaporation value of the Class A Pan as is given in FAO Irrigation and Drainage paper No. 24 (1974), or
ER = M2 - M1 + kp EoER = effective rainfall
Eo = U.S. Class A Open Pan evaporation value M1 and
M2 = moisture status in the effective root zone before and after rain, respectively
kp = pan coefficient
The method takes into account the soil and the crop characteristics. The determination is simple and accurate but it may involve errors due to soil variation; the sampling errors may range from 5 to 40 percent. The method is also laborious and time consuming. The use of neutron probes reduces the drudgery of periodic soil sampling, but these are costly methods for routine purposes and also subject to sampling errors.
A daily soil water balance is rather like a bank account. Rainfall and irrigation are on the credit side, while soil moisture depletion is on the debit side. Precise data on the maximum water holding capacity (field capacity) is necessary for this method. Any amount in excess of this capacity is a surplus and will be a deep percolation loss or run-off. When the balance reaches nil, no more withdrawal is possible and hence further depletion is treated as water deficiency. Rainfall and irrigation are directly measured while the evapotranspiration is computed from any of several available formulae.
In irrigated agriculture, the soil water content is never allowed to fall below a certain value where water becomes a limiting factor in crop production. When water is depleted to the lower limit of readily available moisture, irrigation is applied. Hence, computations may be based on potential evapotranspiration (ETp).
In rainfed or partially irrigated areas, where the soil moisture is depleted below the lower limit of readily available moisture, the computations are to be based on actual evapotranspiration. ETa can be estimated by using the Thornthwaite and Mather method (l955), that of Baier and Robertson (1966), or the relationships between ETa and ETp under decreasing soil water content as given by Tanner (1967).
A sample calculation is given below. The water storage capacity of the soil has been assumed to be 100 mm; irrigation is applied at 50 percent of total depletion. All values are in mm. Of total rainfall of 625 mm, only 279 mm is effective in this case, which amounts to about 45 percent.
|
Date |
Rainfall |
ETp |
Storage change in soil |
Storage balance in soil |
Irrigation |
Water surplus (Drainage) |
|
1 |
100 |
6 |
94 |
94 |
- |
0 |
|
2 |
25 |
8 |
17 |
100 |
- |
11 |
|
3 |
0 |
9 |
-9 |
91 |
- |
0 |
|
4 |
0 |
9 |
-9 |
82 |
- |
0 |
|
5 |
0 |
8 |
-8 |
74 |
- |
0 |
|
6 |
0 |
9 |
-9 |
65 |
- |
0 |
|
7 |
100 |
5 |
95 |
100 |
|
60 |
|
8 |
100 |
4 |
96 |
100 |
- |
96 |
|
9 |
50 |
8 |
42 |
100 |
- |
42 |
|
10 |
0 |
10 |
-10 |
90 |
- |
0 |
|
11 |
0 |
11 |
-11 |
79 |
- |
0 |
|
12 |
0 |
11 |
-11 |
68 |
|
0 |
|
13 |
0 |
12 |
-12 |
56 |
- |
0 |
|
14 |
0 |
12 |
-12 |
44 |
50 |
0 |
|
15 |
0 |
11 |
-11 |
63 |
|
0 |
|
16 |
0 |
11 |
-11 |
72 |
- |
0 |
|
17 |
0 |
10 |
-10 |
62 |
|
0 |
|
18 |
0 |
11 |
-11 |
51 |
- |
0 |
|
19 |
0 |
10 |
-10 |
41 |
50 |
0 |
|
20 |
0 |
10 |
-10 |
81 |
- |
0 |
... Sample calculation continued
|
Date |
Rainfall |
ETp |
Storage change in soil |
Storage balance in soil |
Irrigation |
Water surplus (Drainage) |
|
21 |
0 |
11 |
-11 |
70 |
- |
0 |
|
22 |
0 |
12 |
-12 |
58 |
- |
0 |
|
23 |
0 |
12 |
-12 |
46 |
- |
0 |
|
24 |
50 |
8 |
42 |
- |
88 |
0 |
|
25 |
100 |
6 |
94 |
100 |
- |
82 |
|
26 |
100 |
5 |
59 |
100 |
|
95 |
|
27 |
0 |
10 |
-10 |
90 |
- |
0 |
|
28 |
0 |
10 |
-10 |
80 |
- |
0 |
|
29 |
0 |
10 |
-10 |
70 |
- |
0 |
|
30 |
0 |
10 |
-10 |
60 |
- |
0 |
|
Total |
625 |
279 |
|
|
188 |
386 |
The method is shown in Fig 3. It consists of a rainfall receiver (R) which is connected to a water reservoir (WR), and which in turn is connected to an evaporating surface (E) representing a crop. The reservoir is provided with an overflow outlet at the top of the side wall (D). The capacity of the reservoir is adjusted to the maximum water holding capacity of the soil in question. The rain water above this maximum capacity flows out and is measured as ineffective rainfall. The evaporating surface loses moisture continuously, creating a fall in the water level in the reservoir, which is graduated so that the moisture balance can be read directly at any time.
The device is simple, practical and useful and can easily be set up in the field. The evaporating surface represents the crop and therefore its size and the porosity of the material are important. The method is described by Stanhill (1958).
Fig 3: INTEGRATING GAUGE FOR MEASURING EFFECTIVE RAINFALL
Ramdas (1960) suggested a direct field method using a small portable device containing soil of the field, so eliminating the necessity of sampling.
Fig 4: RAMDAS APPARATUS FOR MEASURING EFFECTIVE RAINFALL
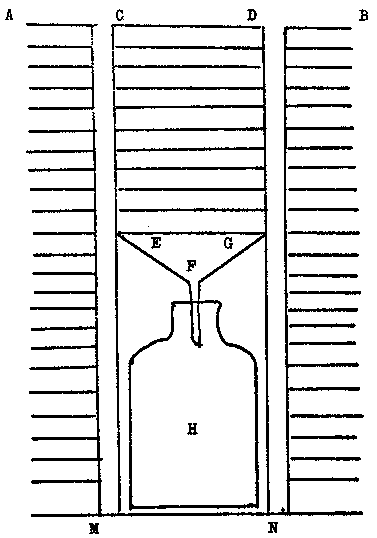
The apparatus, as shown in Fig 4, consists of a cylinder (CD) of about 30 cm in diameter, with a perforated base (BO) and a funnel (F) leading into a receiver bottle (H). All these parts are enclosed in an outer cylinder (MN). The cylinder (CD) is filled with a representative soil with the same density as that of the field. The height is equal to the depth of the effective root zone of the crop. The apparatus is installed in the field crop where the effective rainfall is to be measured. The crop in the container is irrigated along with the field crop. Excess rain or irrigation water drains in the receiver bottle H and is measured from time to time. The total rainfall minus the ineffective rainfall gives the value of effective rainfall. It is assumed that there is no surface run-off. Cylinders of different lengths are used consistent with the rooting depth of the different crops. With a suitable number of replications, the method is very useful. It is simple and practical, and furnishes direct readings.
Lysimetry is a method which provides complete information on all the components of water balance. Lysimeters can be used not only for measuring evapotranspiration but also for checking empirical formulae for computing ET. The method is similar to the Ramdas method, but is more elaborate, refined and gives a higher accuracy.
A lysimeter is a large container with soil in which crops are grown; water losses and gains can be measured. The container is fitted with suitable inlets for irrigation and outlets for drainage. The lysimeters are buried in the field and are surrounded by the same crop as is grown inside. The size of lysimeter varies from small oil drums (Gilbert and van Bavel, 1954) to large size and deep lysimeters (Harrold and Dreilbelbis, 1958, l967 Pruitt and Angus, 1960, McIlroy and Angus, 1963). They can be either the non-weighing or weighing type.
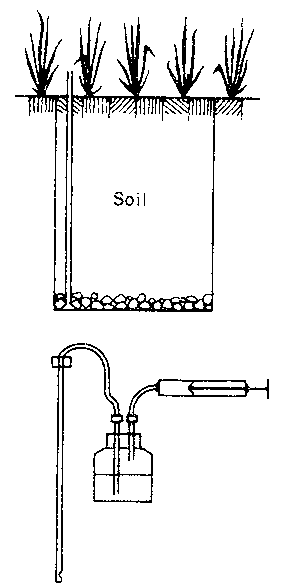
In non-weighing lysimeters, changes in water balance are measured volumetrically weekly or biweekly. No accurate daily estimates can be obtained. A simple design is shown in Pig 5. Irrigation water is applied to the lysimeter, A layer of pebbles is placed at the bottom to facilitate easy drainage. Excess water is collected from below at a suitable distance. A number of crops can be grown in a concentric pattern around a central drainage chamber. A simple lysimeter can be built at low cost from a petrol drum. A tube with a small diameter is placed through the soil to the layer of pebbles. Excess water is removed at frequent intervals by using a thin metal tube open at the bottom which is connected to a receiver bottle in which suction can be applied using a reversed handpump. This is shown in Pig 6.
Weighing lysimeters can provide precise information on soil moisture changes for daily or even hourly periods. The lysimeter is placed inside another tank which is in contact with the surrounding soil. The inside container is free for weighing by scales. Also, the lysimeter tank can be floated in water; a suitable heavy liquid (ZnCl2) is used whereby the change in liquid displacement is a measure for the water gain or loss to or from the lysimeter tank. Apart from the high cost, the major problems with lysimeters are the restricted root growth, the disturbed soil structure in the lysimeter causing changes in water movement and possibly the tank temperature regime, resulting in condensation of water on the walls of the container. Harrold and Dreilbelbis (1967) estimated that errors due to dew formation were in the order of 250 mm per annum. Other limitations include the 'bouquet effect' whereby the canopy of the plants grown in the lysimeter is above and extends over the surrounding crop, resulting in a higher evapotranspiration rate. In spite of these limitations, it is the best technique for precise studies on evapotranspiration.
Fig 5: DRAINAGE LYSIMETER
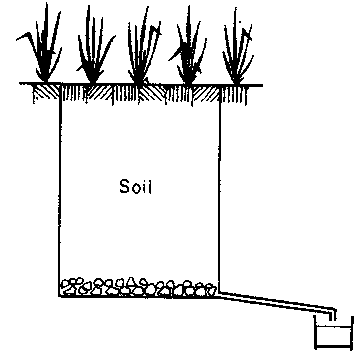
Fig 6: SUCTION TYPE DRAINAGE LYSIMETER
Dastane et al (1966) used a container or drum technique for assessing evapotranspiration, percolation, water requirements and also ineffective rainfall of a rice crop, (Fig 7). Three containers (drums) A, B, and C, of about 40 gallons capacity, 50 cm in diameter and 125 cm high) are embedded in a rice field leaving about a quarter of their height above ground level. The bottoms of containers B and C have been removed. To container C, outlet pipes are fitted at 0,5 cm intervals or a sliding strip is fitted for precise water control.
Fig 7: CONTAINER TECHNIQUE FOR DETERMINATION OF EFFECTIVE RAINFALL IN RICE
The outlet pipes can he connected to a water receiver. The containers are filled with soil and rice is grown inside, along with the adjoining field crop. Water levels in the drums are maintained at the same level as outside. The difference in the values on two successive days caused by the daily loss of water in container A, represents evapotranspiration, while in container B, it indicates daily total needs of water. The daily difference between water levels in containers A and B is percolation loss.
Container C is intended to assess ineffective rainfall. The maximum depth of submergence is governed by the height of the rice crop and height of the field bunds, whichever is less. Any rainfall which submerges the crop beyond a certain critical height or which exceeds the height of the bunds is ineffective. As the height of the crop increases, the outlets are plugged or the sliding strip is pushed progressively upwards till the bund height becomes the limiting factor.
The water level is set at a selected height in container C. This height can be adjusted with increase in growth of plants. Evapotranspiration and percolation continue and create a deficit every day. When rain falls, it first makes up this deficit. When it becomes excessive, the surplus flows out through the outlet pipes. This is the ineffective rainfall. The difference between water levels in containers B and C is ineffective rainfall. If there are no rains, the water level in container C will gradually reach the soil surface and the crop will be irrigated according to routine practice. The technique is simple, inexpensive, easy and practicable. A typical example is given below using a daily balance sheet.
|
Date |
Irrigation |
Daily rain fall |
Drum |
Evapotranspiration ETA |
ETA plus percolation |
Percolation |
Ineffective rainfall |
||
|
A |
B |
C |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Previous day |
0 |
0 |
75 |
75 |
75 |
0 |
0 |
0 |
0 |
|
1 |
0 |
20 |
90 |
80 |
75 |
5 |
15 |
10 |
5 |
|
2 |
0 |
40 |
107 |
97 |
75 |
8 |
18 |
10 |
22 |
|
3 |
0 |
100 |
170 |
160 |
75 |
5 |
15 |
10 |
85 |
|
4 |
0 |
15 |
85 |
75 |
75 |
5 |
15 |
10 |
0 |
|
5 |
0 |
0 |
67 |
75 |
57 |
8 |
18 |
10 |
0 |
|
6 |
0 |
0 |
48 |
38 |
38 |
9 |
19 |
10 |
0 |
|
7 |
0 |
20 |
51 |
41 |
41 |
7 |
17 |
10 |
0 |
|
8 |
0 |
60 |
95 |
85 |
75 |
6 |
16 |
|
10 |
|
9 |
0 |
70 |
140 |
130 |
75 |
5 |
15 |
10 |
55 |
|
10 |
0 |
0 |
67 |
57 |
57 |
8 |
18 |
10 |
0 |
|
11 |
0 |
0 |
49 |
39 |
39 |
8 |
18 |
10 |
0 |
|
12 |
0 |
0 |
32 |
22 |
22 |
7 |
17 |
10 |
0 |
|
13 |
0 |
0 |
17 |
7 |
7 |
5 |
15 |
10 |
0 |
|
14 |
75 |
0 |
75 |
65 |
65 |
7 |
17 |
10 |
0 |
|
15 |
0 |
30 |
90 |
80 |
75 |
5 |
15 |
10 |
5 |
|
Total |
75 |
355 |
- |
- |
- |
98 |
248 |
150 |
182 |
Permissible water depth = 75 mm
Column 2: from water meter reading
Column 3: from rain gauge records
Columns 4 to be adjusted daily to column 6 reading and 5: and to be observed next day
Column 6: reading from daily observations
Column 7: previous day's column 6 plus column 3 minus column 4
Column 8: previous day's column 6 plus column 3 minus column 5
Column 9: column 8 minus column 7
Column 10: column 5 minus column 6
3.1 Renfro Equation
3.2 U.S. Bureau of Reclamation Method
3.3 Potential Evapotranspiration/Precipitation Ratio Method (India)
3.4 USDA, SCS Method
3.5 Empirical Relationships
A number of empirically determined formulae can be used. They have been developed under a given set of conditions which may be very different from those under which they are to be applied. Their use elsewhere therefore remains doubtful.
Renfro, as quoted by Chow (1964), suggested the following equation for estimating effective rainfall:
ER = E Rg + A
ER = effective rainfall
Rg = growing season rainfall
A = average irrigation application
E = ratio of consumptive use of water (CU) to rainfall during the growing season (Table 4)
The E value implies degree of rain likely to be utilized in meeting consumptive water needs. The greater the E value, the higher the value of effective rainfall. For example, if rainfall during the four month growing season is 400 mm, consumptive use of water is 700 mm, and average irrigation application is 100 mm, then the effective rainfall is equal to 0.60 x 400 + 100 - 340 mm. The method is empirical and may not suit many situations.
Table 4: RATIO E FOR USE IN ESTIMATING EFFECTIVE RAINFALL IN RENFRO EQUATION (Chow, 1964)
|
CU/Rg |
E |
CU/Rg |
E |
|
0 |
0 |
2.4 |
0.72 |
|
0.2 |
0.10 |
2.6 |
0.75 |
|
0.4 |
0.19 |
2.8 |
0.77 |
|
0.6 |
0.27 |
3.0 |
0.80 |
|
0.8 |
0.35 |
3.5 |
0.84 |
|
1.0 |
0.41 |
4.0 |
0.88 |
|
1.2 |
0.47 |
4.5 |
0.91 |
|
1.4 |
0.52 |
5.0 |
0.93 |
|
1.6 |
0.57 |
6.0 |
0.96 |
|
1.8 |
0.61 |
7.0 |
0.98 |
|
2.0 |
0.65 |
9.0 |
0.99 |
|
2.2 |
0.69 |
/ |
I |
A method described by Stamm (1967), is recommended for arid and semi-arid regions and uses mean seasonal precipitation of the five driest consecutive years. Percentage marks are given to increments of monthly rainfall ranging from greater than 90 percent for the first 25 mm (1 in) or fraction thereof, to 0 percent for precipitation increments above some 150 mm (6 in), as is shown in Table 5.
Table 5: EFFECTIVE PRECIPITATION BASED ON INCREMENTS OF MONTHLY RAINFALL (U.S. BUREAU OF RECLAMATION METHOD)
|
Precipitation increment range |
Percent |
Effective precipitation accumulated - range |
||
|
mm |
in |
mm |
in |
|
|
0.0 - 25.4 |
0 - 1 |
90-100 |
22.9 - 25.4 |
0.90 - 1.00 |
|
25.4 - 50.8 |
1 - 2 |
85 - 95 |
44.4 - 49.5 |
1.75 - 1.95 |
|
50.8 - 76.2 |
2-3 |
75 - 90 |
63.5 - 72.4 |
2.50 - 2.85 |
|
76.2 - 101.6 |
3-4 |
50-80 |
76.2 - 92.7 |
3.00 - 3.65 |
|
101.6 - 127.0 |
4-5 |
30-60 |
83.8 - 107.9 |
3.30 - 4.25 |
|
127.0 - 152.4 |
5-6 |
10 - 40 |
86.4 - 118.1 |
3.40 - 4.65 |
|
Over 152.4 |
Over 6 |
0-10 |
86.4 - 120.6 |
3.40 - 4.75 |
For example, if monthly rainfall during the past five years in the month of July is 100; 125; 250; 225 and 175 cm, the mean is 175 cm. From the table, the effective rainfall value for the month of July will be 120.6 mm. The method does not take into account the type of soil, nature of the crop and frequency and distribution of rain. Nor does it consider degree of aridity. The method is not considered satisfactory.
This simple semi-empirical method is used in some projects in India. A ratio of potential evapotranspiration, taken as 0.8 of the U.S. Class A pan data, to the total rainfall for a certain group of days during the growing season is computed. The number of days in a group is based broadly on a soil type or soil moisture properties as well as general weather conditions or evapotranspiration rates* The maximum number of days in a group is 15 during warm weather and 30 during cool weather for crops other than rice. The lower the water holding capacity of the soil and/or the higher the evapotranspiration rate, the shorter the period in the group. This is shown in Table 6.
Table 6: NUMBER OF DAYS IN A GROUP FOR DIFFERENT SOIL TYPES AND CLIMATIC CONDITIONS
|
Crop |
Mean monthly ETp (mm/day) |
Soil texture and water storage capacity (mm/m). |
|||
|
Light (below 40) |
Medium (40 to 80) |
Heavy (80 to 120) |
Very heavy (over 120) |
||
|
Rice |
3 to 12 |
2 |
3 |
4 |
7 |
|
Other |
Over 6 |
4 |
7 |
10 |
15 |
|
crops |
Below 6 |
7 |
10 |
15 |
30 |
Rainless periods are deleted from the calculations. The ratios are expressed in a percentage for each period. So the maximum value of the ratio cannot exceed 100. The monthly means are then computed and from these the grand mean ratio is obtained for the entire growing season. Precise knowledge on soil properties or aridity is not essential. There can be some under or over estimation depending upon the distribution of rainfall, but the error is small. This method is good for broad planning purposes. It is rapid and inexpensive.
A sample calculation for the case of a heavy soil in a warm season is shown below. Of the total rainfall of 670 mm during the growing season, 80 percent is effective according to this method,
|
Period |
Potential evapotranspiration (mm) |
Rainfall (mm) |
Percentage ratio |
Mean ratio for the month(%) |
|
July 1-10 |
60 |
80 |
75 |
|
|
11-20 |
80 |
0 |
0 |
87 |
|
21 - 31 |
65 |
60 |
100 |
|
|
Aug. 1 - 10 |
60 |
150 |
40 |
|
|
11-20 |
65 |
100 |
65 |
60 |
|
21 - 31 |
60 |
80 |
75 |
|
|
Sept. 1 - 10 |
60 |
60 |
100 |
|
|
11 - 20 |
70 |
40 |
100 |
100 |
|
21 - 30 |
80 |
20 |
100 |
|
|
Oct. 1 - 10 |
80 |
0 |
0 |
|
|
11 - 20 |
85 |
0 |
0 |
75 |
|
21 - 31 |
60 |
80 |
75 |
|
|
Total |
825 |
670 |
- |
322 |
|
Mean |
... |
... |
... |
80% |
In the case of rice, instead of the evapotranspiration value, total water loss, which is evapotranspiration plus percolation losses, is used for computation.
Taking crop characteristics into account, necessary correction can be further applied for undesirable or destructive kinds of rainfall such as those causing lodging, or flower or fruit drop.
The U.S. Department of Agriculture's Soil Conservation Service has developed a procedure for estimating effective rainfall by processing long term climatic and soil moisture data. A comprehensive analysis was made by perusing 50 years of precipitation records at 22 experimental stations representing different climatic and soil conditions. The soil moisture balance was worked out for each day try adding effective rainfall or irrigation to the previous day's balance and subtracting consumptive use. To avoid a high degree of complexity, neither the soil intake rate nor rainfall intensities are considered in this method.
From total rainfall and monthly consumptive use, effective rainfall values were computed (Table 6). The values were based on a 3 in or 75 mm net irrigation application, which is equal to the available storage capacity in the root zone at the time of irrigation application. To convert this data to other net depths, factors were worked out which are shown in Table 7. For example, a crop of wheat grown on sandy loam has a net depth of irrigation application of 50 ram. With a mean consumptive use for the month of December of 100 mm and a mean rainfall of 75 mm, the effective rainfall will be 52.7 x 0.93 = 49 mm.
The monthly effective rainfall cannot exceed the rate of consumptive use. If it does, the lower value of the two is taken.
Table 7: MULTIPLICATION FACTORS TO RELATE MONTHLY EFFECTIVE RAINFALL VALUE OBTAINED FROM TABLE 8 TO NET DEPTH OF IRRIGATION APPLICATION (d), IN mm
|
d mm |
factor |
d mm |
factor |
d mm |
factor |
|
10.00 |
0.620 |
31.25 |
0.818 |
70.00 |
0.990 |
|
12.50 |
0.650 |
32.50 |
0.826 |
75.00 |
1.000 |
|
15.00 |
0.676 |
35.00 |
0.842 |
80.00 |
1.004 |
|
17.50 |
0.703 |
37.50 |
0.360 |
85.00 |
1.008 |
|
18.75 |
0.720 |
40.00 |
0.876 |
90.00 |
1.012 |
|
20.00 |
0.728 |
45.00 |
0.905 |
95.00 |
1.016 |
|
22.50 |
0.749 |
50.00 |
0.930 |
100.00 |
1.020 |
|
25.00 |
0.770 |
55.00 |
0.947 |
125.00 |
1.040 |
|
27.50 |
0.790 |
60.00 |
0.963 |
150.00 |
1.060 |
|
30.00 |
0.808 |
65.00 |
0.977 |
175.00 |
1.070 |
Table 8: AVERAGE MONTHLY EFFECTIVE RAINFALL AS RELATED TO MEAN MONTHLY RAINFALL AND MEAN MONTHLY CONSUMPTIVE USE (USDA, SCS)
|
Monthly mean rainfall mm |
Mean monthly consumptive use mm |
|||||||||||||
|
25 |
50 |
75 |
100 |
125 |
150 |
175 |
200 |
225 |
250 |
275 |
300 |
325 |
350 |
|
|
Mean monthly effective rainfall mm |
||||||||||||||
|
12.5 |
7.5 |
8.0 |
8.7 |
9.0 |
9.2 |
10.0 |
10.5 |
11.2 |
11.7 |
12.5 |
12.5 |
12.5 |
12.5 |
12.5 |
|
25.0 |
15.0 |
16.2 |
17.5 |
18.0 |
18.5 |
19.7 |
20.5 |
22.0 |
24.5 |
25.0 |
25.0 |
25.0 |
25.0 |
25.0 |
|
37.5 |
22.5 |
24.0 |
26.2 |
27.5 |
28.2 |
29.2 |
30.5 |
33.0 |
36.2 |
37.5 |
37.5 |
37.5 |
37.5 |
37.5 |
|
50.0 |
25 |
32.2 |
34.5 |
35.7 |
36.7 |
39.0 |
40.5 |
43.7 |
47.0 |
50.0 |
50.0 |
50.0 |
50.0 |
50.0 |
|
62.5 |
at 41.7 |
39.7 |
42.5 |
44.5 |
46.0 |
48.5 |
50.5 |
53.7 |
57.5 |
62.5 |
62.5 |
62.5 |
62.5 |
62.5 |
|
75.0 |
|
46.2 |
49.7 |
52.7 |
55.0 |
57.5 |
60.2 |
63.7 |
67.5 |
73.7 |
75.0 |
75.0 |
75.0 |
75.0 |
|
87.5 |
|
50.0 |
56.7 |
60.2 |
63.7 |
66.0 |
69.7 |
73.7 |
77.7 |
84.5 |
87.5 |
87.5 |
87.5 |
87.5 |
|
100.0 |
|
at 80.7 |
63.7 |
67.7 |
72.0 |
74.2 |
78.7 |
83.0 |
87.7 |
95.0 |
100 |
100 |
100 |
100 |
|
112.5 |
|
|
70.5 |
75.0 |
80.2 |
82.5 |
87.2 |
92.7 |
98.0 |
105 |
111 |
112 |
112 |
112 |
|
125.0 |
|
|
75.0 |
81.5 |
87.7 |
90.5 |
95.7 |
102 |
108 |
115 |
121 |
125 |
125 |
125 |
|
137.5 |
|
|
at 122 |
88.7 |
95.2 |
98.7 |
104 |
111 |
118 |
126 |
132 |
137 |
137 |
137 |
|
150.0 |
|
|
|
95.2 |
102 |
106 |
112 |
120 |
127 |
136 |
143 |
150 |
150 |
150 |
|
162.5 |
|
|
|
100 |
109 |
113 |
120 |
128 |
135 |
145 |
153 |
160 |
162 |
162 |
|
175.0 |
|
|
|
at 160 |
115 |
120 |
127 |
135 |
143 |
154 |
164 |
170 |
175 |
175 |
|
187.5 |
|
|
|
|
121 |
126 |
134 |
142 |
151 |
161 |
170 |
179 |
185 |
187 |
|
200.0 |
|
|
|
|
125 |
133 |
140 |
148 |
158 |
168 |
178 |
188 |
196 |
200 |
|
225 |
|
|
|
|
at 197 |
144 |
151 |
160 |
171 |
182 |
|
|
|
|
|
250 |
|
|
|
|
|
150 |
161 |
170 |
183 |
194 |
|
|
|
|
|
275 |
|
|
|
|
|
at 240 |
171 |
181 |
194 |
205 |
|
|
|
|
|
300 |
|
|
|
|
|
|
175 |
190 |
203 |
215 |
|
|
|
|
|
325 |
|
|
|
|
|
|
at 287 |
198 |
213 |
224 |
|
|
|
|
|
350 |
|
|
|
|
|
|
|
200 |
220 |
232 |
|
|
|
|
|
375 |
|
|
|
|
|
|
|
at 331 |
225 |
240 |
|
|
|
|
|
400 |
|
|
|
|
|
|
|
|
at 372 |
247 |
|
|
|
|
|
425 |
|
|
|
|
|
|
|
|
|
250 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
at 412 |
|
|
|
|
|
450 |
25 |
50 |
75 |
100 |
125 |
150 |
175 |
200 |
225 |
250 |
|
|
|
|
Several methods of estimating effective rainfall for irrigation schedules are in vogue in different countries. They are based on long experience and have been found to work quite satisfactorily in the specific conditions under which they were developed.
India
For a given area, effective rainfall is taken to be equal to 70 percent of the average seasonal rainfall.
In another method, effective rainfall is taken as the mean value of rain, with the excess ever 3 in. in one day and 5 in. in 10 days omitted.
Effective rainfall has also been taken to be equal to the lowest monsoon rainfall occurring in three out of four years.
The Damodar Valley Corporation divided the 'Kharip season' (June to November) into ten-day periods. During these periods, rainfall which exceeded the water needs of the predominant crop was considered as ineffective and the rest as effective.
Khushlani (1956) suggested that rainfall during the life cycle of the crop in a bad year (one with low rainfall) should be considered as the effective rainfall.
In determining the water requirement of sugar cane under Bombay Deccan conditions, Rege et al (1943) considered that rainfall received only after five days from the irrigation date was effective. The rainfall received within five day after irrigation was treated as ineffective.
Sastry (1956) suggested the following equation for estimating rainfall usable by crops under Andhra Pradesh (central part of South India) conditions,
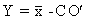Y = usable rainfall, per days for a given period= mean dally rainfall
C = a constant, which determines the confidence limit of the minimum statistical average
d = standard deviation of the dally rainfall
Estimates of usable rainfall in various periods of the monsoon season can be arrived at by selecting suitable confidence limits and statistical methods for calculating the standard deviation.
Burma
During the wet season, rainfall of less than 0.5 in. is considered as ineffective. Above this figure, 63 percent of the amount greater than 0,5 in. is considered affective rainfall. Baring the dry season, rainfall of less than 1 in. is considered as ineffective. Above this figure, 65 percent of the amount greater than 1 in. is considered as. usable by the crop (Kung, 1971). This approach would appear to be rather arbitrary.
Thailand
Of the November rainfall 80 percent and of the December to March rainfall 90 percent is considered an effective (Kung, 1971)
3.5.2 Rice Measurement in rice
Rice thrives under conditions of abundant water supply, hence the practice of land submergence. Depth of flooding is governed by the variety grown and its height, the height of field bunds and availability of water. The water requirements of rice include evapotranspiration and percolation. Measuring effective rainfall is thus more complicated. Different empirical methods used in different countries are outlined below (Kung, 1971).
India
In one method, a percentage of total rainfall varying from 50 to 80 percent is assumed effective.
In a second method, rainfall less than 0.25 in (6.25 mm) on any day is considered as ineffective* Similarly any amount over 3 in (75 mm) per day, and rainfall in excess of 5 in (125 mm) in 10 days is treated as ineffective.
Japan
For submerged rice the year having the lowest rainfall over the past 10 to 15 years is selected. Depending upon local conditions, an amount of 50 to 80 mm is considered as ineffective. The rest is all effective. A daily record is kept of soil water in the field.
For non-submerged rice a method using daily readings is also used. The daily rainfall efficiency is assumed to be 80 percent. Daily rainfall of less than 0.5 x ET is not effective. Also, if the sum of effective rainfall and the residual moisture from the previous day exceeds a predetermined value, the surplus is disregarded. A sample calculation of computation for a 12 day period is shown below for non-submerged rice. In this example ET = 3.7 mm/day, available soil Water = 30 mm.
|
Date |
Rainfall (A) |
Effective rainfall |
Potential evapotranspiration |
Soil water storage change |
Irrigation applied |
Stored soil water balance |
Remarks |
|
1 |
0 |
0 |
3.7 |
-3.7 |
30.0 |
26.3 |
|
|
2 |
1.7 |
0 |
3.7 |
-3.7 |
0 |
22.6 |
(1.7 x 0.8) less than 1.85 |
|
3 |
5.4 |
4.3 |
3.7 |
+0.6 |
0 |
23.2 |
|
|
4 |
0 |
0 |
3.7 |
-3.7 |
0 |
19.5 |
|
|
5 |
1.5 |
0 |
3.7 |
-3.7 |
0 |
15.8 |
(1.5 x 0.8) less than 1.85 |
|
6 |
5.8 |
4.6 |
3.7 |
+0.9 |
0 |
16.7 |
|
|
7 |
0 |
0 |
3.7 |
-3.7 |
0 |
13.0 |
|
|
8 |
0 |
0 |
3.7 |
-3.7 |
0 |
9.3 |
|
|
9 |
53.2 |
20.7 |
3.7 |
+17.0 |
0 |
26.3 |
(53.2 x 0.8) + 9.3 greater than 30.0 |
|
10 |
2.5 |
2.0 |
3.7 |
-1.7 |
0 |
24.6 |
|
|
11 |
20.3 |
5.4 |
3.7 |
+1.7 |
0 |
26.3 |
(30.0 - 24.6)- 5.4 |
|
12 |
35.0 |
3.7 |
3.7 |
0.0 |
0 |
26.3 |
(30.0 - 26.3)- 3.7 |
The method must be modified in respect of rainfall efficiency, the moisture storage capacity of the soil, and evapotranspiration, before it can be used for other situations.
Vietnam
The water holding capacity of rice soils is assumed to be 50 mm. Daily rainfall below 5 mm and above 50 mm is disregarded. If daily evapotranspiration is 10 mm, a two-days' successive rainfall of up to 60 mm is taken as effective and excess over this limit is disregarded. Similarly, three days' successive rainfall of up to 70 mm is taken as effective and the excess is disregarded. The same procedure is followed for more rainy days.
In different months different percentages are considered to be effective out of the total rainfall received.
|
Period |
% taken as effective |
Remarks |
|
April - September |
75 |
Wet season |
|
October |
65 |
High rainfall intensity |
|
November |
80 |
Dry season |
|
December - March |
90 |
Dry and cool season |
Burma
Rainfall below 0.5 in is considered as ineffective. Above 0.5 in, 80 percent of the amount in excess is considered as effective.
A method must account satisfactorily for surface run-off, water storage changes in the soil, evapotranspiration and crop characteristics. For field use, the method should be simple, inexpensive, rapid and accurate. It should be useful for broad regional planning or precise irrigation scheduling under a given set of conditions. For each method measurement of total rainfall using & rain gauge or rain recorder is essential. Relative merits and limitations of the different methods discussed are shown in Table 9. Of the field methods, the first method (No.2.1) involving periodic measurement of soil water changed is accurate only when a sufficient number of replications are made; it is very laborious and cumbersome for field application. The method can be used to verify the applicability of empirical methods developed elsewhere. The soil water balance sheet method (No.2.2) involving the use of meteorological data and estimation of ETa will provide data on estimating effective rainfall if relevant input data are available. The estimation of ETa, however, is more complicated and less accurate than the estimation of ETp. In the integrating gauge method (No.2.3), ceramic plates are used; the relation between evaporation from the plate and the evapotranspiration from the crop must be known but is difficult to establish. Errors are due to dust and salt accumulation on the evaporating surface, The Ramdas method (No.2.4) is simple bat may not be accurate unless a large number of replications are made. This may make the method cumbersome for field use. The use of lysimeters of large diameters (No.2.5) is the best and the most reliable method in assessment of effective rainfall. It is, however, expensive for field use. It should be installed in research stations. The method can be used to check the accuracy of the other methods. The drum technique for rice (No.2.6) has given promising results. The method requires replications to give accurate data.
Of the empirical formulae the Renfro equation method (No. 3.1) is too empirical. The U.S. Bureau of Reclamation method (NO. 3.2) neglects many essential parameters. The method based on the ratio of potential evapotranspiration to precipitation (No.3.3) will provide the best results. It can be used for broad estimation of effective rainfall in irrigation planning. The USDA, SCS method (NO. 3.4) has been based on data representing a wide range of conditions. The method is satisfactory and can be applied for field use after verification in a given situation. The empirical methods for crops other than rice (No.3.5.1) and for rice (No.3.5.2), are based on long experience. They may be satisfactory under local conditions but need verification when applied in conditions very different from those under which they were developed.
Methods described under 2.2, 3.3, 3.4, and 3.5.1 when used in planning should first be checked for accuracy using methods 2.1 or 2.5. The choice of method to be used depends upon the funds, facilities and basic data that are locally available.
Table 9: RELATIVE MERITS OF DIFFERENT METHODS FOR DETERMINING EFFECTIVE RAINFALL
|
Methods |
Factors taken into account |
Special equipment |
Accuracy |
Relative costs |
Remarks |
|||
|
Run-off |
Soil |
Aridity |
Crop |
|||||
|
2.1 Field studies of soil moisture |
+ |
+ |
+ |
+ |
+ |
Very high |
Medium |
Good for verifying other met hods; cumbersome practicability low |
|
2.2 Daily soil water budget with Eta |
- |
+ |
+ |
|
+ |
Very high |
Medium |
Practicability medium |
|
2.3 Integrating gauge |
- |
+ |
+ |
+ |
+ |
Medium |
Medium |
Needs careful standardization |
|
2.4 Ramdas apparatus |
- |
+ |
+ |
+ |
+ |
High |
Medium |
Practicability good |
|
2.3 Lysimeters |
- |
+ |
+ |
+ |
+ |
Very high |
Very high |
Practicability medium, good as a check on other methods |
|
2.6 Drum technique (rice) |
+ |
+ |
+ |
+ |
+ |
Very high |
Low |
Practicability high |
|
3.1 Renfro equation |
- |
B |
+ |
- |
+ |
Low |
Negligible |
Too empirical |
|
3.2 U.S. Bureau of Reclamation method |
+ |
- |
- |
- |
- |
Low |
Negligible |
Not suitable for wide use |
|
3.3 Ratio of ETp to precipitation |
B |
B |
+ |
- |
- |
Medium |
Low |
Satisfactory for very preliminary planning purposes |
|
3.4 USDA, SCS method |
- |
B |
+ |
B |
- |
Medium |
Low |
Good for areas with low intensity of rainfall and high soil infiltration rate |
|
3.5.1 Empirical methods (other than rice) |
B |
B |
B |
B |
- |
Low to high |
Negligible |
Practicability very high |
|
3.5.2 Empirical methods (rice) |
B |
B |
B |
B |
- |
Medium |
Negligible |
Needs verification; practicability high |
+ = positive; - = negative; B = first approximation
