La science construit des modèles ou théories pour expliquer les phénomènes. Les phénomènes sont observés et des relations, des causes et des explications sont recherchées. Les observations sont réalisées sur l’évolution des grandeurs (caractéristiques) par rapport au temps (ou à d’autres caractéristiques) et en tenant compte des causes (facteurs) possibles.
Physique - phénomène du mouvement des corps (caractéristiques - espaces parcourus par rapport aux temps dépensés à les parcourir)
Biologie - phénomène de la croissance (caractéristique - longueur ou poids, par rapport au temps)
2.1.1 Structure d’un modele
Suppositions de base
elles simplifient la réalité
elles doivent être simples et “traitables” mathématiquement
elles ne peuvent pas être contradictoires
elles ne se démontrent pas
elles sont établies sur les caractéristiques
Les suppositions de base se reportent normalement à l’évolution des caractéristiques et sont établies à partir des taux de variation de ces caractéristiques.
Relations (propriétés)
déduites à partir des suppositions de base ou des relations déduites antérieurement par les lois de la logique (mathématique). Les propriétés sont aussi désignées par:
“résultats” ou “conclusions” du modèle
Vérification
les résultats du modèle doivent être cohérents (concorder avec la réalité)
la vérification suppose l’observation (pratique):
échantillonnage, méthodes statistiques,...
Perfectionnement
si les résultats ne s’accordent pas avec la réalité il faut changer les suppositions de base
si l’accord s’en rapproche il faut vérifier si le rapprochement est suffisant ou non.
le changement des suppositions de base peut être juste un “élargissement de contexte” de la réalité qui a servi de base aux suppositions pour les adapter à la nouvelle réalité sur laquelle on prétend appliquer le modèle.
Avantages
plus simple d’analyser les propriétés du modèle que la réalité
résultats utiles dans le sens pratique
possibilité d’analyser des situations ou des scénarios différents
mettre en évidence l’essentiel des phénomènes et leurs causes
possibilité de perfectionnement
2.1.2 Type de modeles plus couramment utilises en evaluation des peches
Modèles de Production
Les modèles de production sont aussi appelés de modèles de Production Générale, modèles Globaux, modèles Synthétiques ou modèles du type Lotka-Volterra. Ces modèles considèrent le stock dans sa globalité, en particulier l’abondance totale (en poids ou en nombre) et étudient son évolution, les effets de l’effort de pêche, etc. Ils ne considèrent pas la structure par âge ou par longueurs du stock.
Modèles Structuraux
Ces modèles considèrent la structure du stock par âges et l’évolution de cette structure avec le temps. Mais, ils reconnaissent principalement que le stock dans une certaine période de temps est composé par des individus de différentes cohortes, et donc de différents âges et longueurs. Ainsi, ils permettent des analyses et des prévisions de ce qui peut arriver au stock et aux captures, en accompagnant l’évolution des différentes cohortes qui le composent.
Ce manuel ne suivra pas le chemin historique de la construction des modèles. Il a été jugé plus convenant discuter en premier les Modèles Structuraux et après analyser les Modèles de Production.
Les suppositions de base d’un modèle sur l’évolution d’une caractéristique requièrent le concept de taux de variation de la caractéristique par rapport au temps (ou à d’autres caractéristiques).
Figure 2.1 Évolution de la longueur (L) d’un individu avec le temps (ou l’âge) (t)
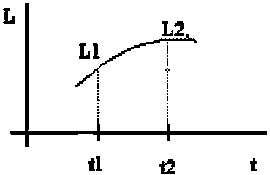
Pour l’étude générale des taux, il faudra substituer la caractéristique L de l’exemple par y, et la variable associée ne sera plus le temps t mais la variable x. En tenant compte des modèles d’évaluation et pour simplifier, on considérera que la fonction y, ne prend que des valeurs réelles et non négatives.
2.2.1 Taux moyen absolu - tma(Y)
Considérez y une fonction de x et l’intervalle i de limites (xi, xi+1)
Figure 2.2 Fonction y=f(x) variant dans l’intervalle i
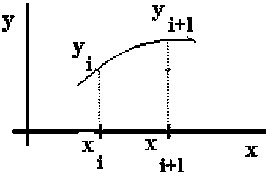
Soient:
Dxi = xi+1 - xi la taille de l’intervalle
yi = valeur de y quand x = xi
yi+1 = valeur de y quand x = xi+1
La variation de y dans l’intervalle Dxi sera Dyi = yi+1 - yi
Le taux moyen absolu, tma(y), de la variation de y dans l’intervalle Dxi sera:
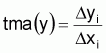
Graphiquement:
Figure 2.3 Taux moyen absolu de variation de y dans l’intervalle Dxi
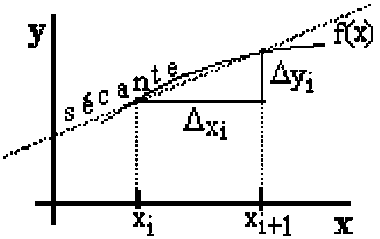
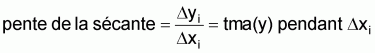
Note: tma(y) est connue en physique comme la vitesse moyenne de variation de y en x, dans l’intervalle Dxi.
2.2.2 TAUX INSTANTANE ABSOLU - tia(y)
Soit y une fonction de x
Le taux instantané absolu de y au point x = xi est la dérivée de y par rapport à x en ce point.
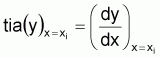
Graphiquement:
Figure 2.4 Taux instantané absolu de y au point xi
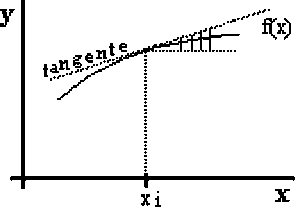
Note: tia(y) est connue comme vitesse instantanée de variation de y en x au point x.
Propriétés
1. Soit tia(y) le calcul de la fonction y est obtenu par intégration, étant y = f(x) + Constante, où f(x) = Primitive de tia(y) et Constante est la constante d’intégration.
Si l’on adopte la condition initiale x*, y*, où y* est la valeur de y correspondante à x = x*, alors, en éliminant la Constante, y = y*+f(x)-f(x*)
2. L’angle que la tangente à la courbe y fait avec l’axe xx’ est désigné par inclinaison.
La tangente trigonométrique de l’inclination est la pente de la tangente géométrique.
tia(y) = dérivée de y = pente = tg (inclinaison)
3. Si en un point x:
tia(y) > 0 alors y est croissant en ce point
tia(y) < 0 alors y est décroissant
tia(y) = 0 alors y est stationnaire en ce point (maximum ou minimum)
4. Si tia(y) = constante = const alors y est fonction linéaire de x, ou de la propriété 1:
y = Constante + const. x ou
y = y* + const.(x-x*) et vice-versa
5. Si y(x) = u(x) + v(x) alors tia(y) = tia(u) + tia(v)
6. Si les causes A et B isolément provoquent des variations en y alors les causes A et B en simultané provoquent une variation en y avec
tia(y) totale = tia(y) cause A + tia(y) cause B
tia(tia(y)) = d2y/dx2 = accélération de y au point x
7. Si l’accélération au point x est positive alors tia(y) est croissante et si cette accélération est négative tia(y) sera décroissante.
2.2.3 TAUX MOYEN RELATIF - tmr(y)
Considérez y une fonction de x et l’intervalle (xi, xi+1)
Soit:
Dxi = xi+1- xi = taille de l’intervalle
yi = valeur de y quand x = xi
yi+1 = valeur de y quand x = xi+1
xi* = un point de l’intervalle (xi, xi+1)
yi* = valeur de y quand x = xi*
Le taux moyen de y par rapport à yi* sera:
ou
Commentaires
1. tmr(y) est associé avec le taux moyen de variation en pourcentage de y par rapport à la moyenne y*, soit,
2. Il est désigné par
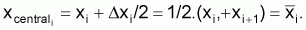
3. Il faut, donc, désigner par
 dans l’intervalle
(xi, xi+1) la valeur de y quand
dans l’intervalle
(xi, xi+1) la valeur de y quand
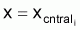
À noter que
 peut être
différent de la moyenne, (yi,+ yi+1)/2.
peut être
différent de la moyenne, (yi,+ yi+1)/2.
4. Il est fréquent de calculer tmr(y) par rapport
à  de
l’intervalle.
de
l’intervalle.
2.2.4 TAUX INSTANTANE RELATIF - tir(y)
Soit y une fonction de x
Le taux relatif instantané de y au point x = xi est
ou
Propriétés
1. Soit tir(y), le calcul de la fonction y est obtenu par intégration, avec y = f(x) + Constante, où f(x) = Primitive de tir(y) et Constante est la constante d’intégration.
Si l'on adopte la condition initiale x*, y*, où y* est la valeur de y correspondante à x = x*, on aura, en éliminant la Constante, y = y*+ f(x) - f(x*)
2. Si à un point x:
tir(y) > 0 alors y est croissant en ce point
tir(y) < 0 alors y est décroissant
tir(y) = 0 alors y est stationnaire en ce point (maximum ou minimum)
3. tir(y) = tia(lny) comme il peut être déduit par les règles de dérivation.
4. Si tir(y) = constante = const alors y est fonction exponentielle de x, soit,
|
y = Constante. econst.x |
ou |
|
|
et vice-versa. |
5. Si y(x) = u(x).v(x) alors tir(y) = tir(u) + tir(v)
6. Si les causes A et B provoquent isolément des variations en y alors les causes A et B en simultané provoquent une variation en y où
tir(y)total = tir(y)cause A + tir(y)cause B
Soit y =f(x)
Supposition de base du modèle
tia(y) = Constante = b dans l’intervalle(xi, xi+1) avec Dxi = xi+1 - xi
Condition initiale
x* = xi Þy* = yi
Figure 2.5 Représentation graphique d’un modèle linéaire simple
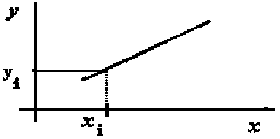
Propriétés
|
1. |
Expression générale |
y = yi + b · (x - xi); y = a + bx |
|
2. |
Valeur, yI+1 à la fin de l’intervalle, Dxi |
yi+1 = yi +b · Dxi |
|
3. |
Variation, Dyi, pendant l’intervalle, Dxi |
Dyi = yi+1 - yi = b. Dxi |
|
4. |
Valeur centrale,
|
|
|
5. |
Valeur accumulée,
|
ou de la Propriété 1
|
|
6. |
Valeur moyenne,
|
|
Autres expressions utiles
|
7. |
Valeur accumulée,
|
|
|
8. |
Valeur moyenne,
|
|
|
9. |
Valeur moyenne,
|
|
|
10. |
Valeur moyenne,
|
|
|
11. |
Relation entre tma(y) et tia(y) |
|
|
12. |
Si |
|
|
13. |
Dans le modèle linéaire la moyenne
arithmétique de |
|
Démonstrations importantes
|
Expression générale |
Si tia(y) = b dans l’intervalle Dxi alors y est linéaire avec x et vu la condition initiale, sera: y = yi+ b.(x-xi) |
|
Valeur centrale |
|
|
Valeur accumulée |
|
|
|
|
Soit y = f(x)
Supposition de base du modèle
tir(y) = Constante = c dans l’intervalle (xi, xi+1), avec Dxi = xi+1 - xi
Condition initiale
x* = xi Þ y* = yi
Propriétés
Vu que tir(y) = tia(lny) on peut dire que le modèle exponentiel de y contre x est équivalent au modèle linéaire de lny contre x. Ainsi, ses propriétés plus importantes peuvent être déduites en anti-logarithmisant les propriétés du modèle linéaire de lny contre x.
Figure 2.6 Représentation graphique du modèle exponentiel
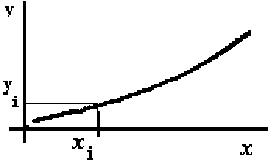
Figure 2.7 Représentation graphique du modèle linéaire de lny contre x
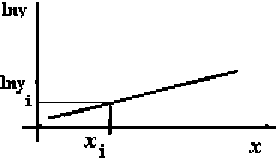
|
|
|
Modèle exponentiel de y |
|
Modèle linéaire de |
|
|
|
(y contre x) |
¬ |
lny (lny contre x) |
|
1. |
Expression générale |
|
¬ |
lny = lnyi+c(x-xi) |
|
2. |
Valeur de yI+1 à la fin de l’intervalle, Dxi |
|
¬ |
lnyi+1= lnyi+cDxI |
|
3. |
Variation, Dyi , durant l’intervalle, Dxi |
|
|
calculé de 1 |
|
4. |
Valeur centrale,
|
|
¬ |
ln |
|
|
|
( |
¬ |
ln |
|
5. |
Valeur accumulée,
|
|
|
|
|
6. |
Valeur moyenne,
|
|
|
(Dyi remplacé par la Propriété 3) |
Autres expressions utiles
|
7. |
Expressions de variation, Dyi |
Dyi = c.
|
|
|
|
8. |
Expression de tma(y) |
|
|
|
|
9. |
Expression de tmr(y) par rapport à
|
|
|
|
|
10. |
Expressions de tmr(y) |
tmr(y) = tma(lny) =
|
|
|
|
11. |
Si |
y décroît c<0 |
et vice-versa |
|
|
12. |
Dans le modèle exponentiel, la moyenne
géométrique de
|
|||
Démonstrations
|
Valeur accumulée |
|
|
Relation entre
|
En utilisant l’approximation
et, donc, par la propriété 4-1ère expression, on conclut que:
|