CHAPITRE 3 - COHORTE

3.1 Cohorte - Introduction

On désigne par cohorte ou classe annuelle ou par génération, un groupe de poissons d’un stock nés la même année. Le schéma suivant illustre les différentes phases du cycle de vie d’une cohorte:

Figure 3.1 Cycle de vie d’une cohorte

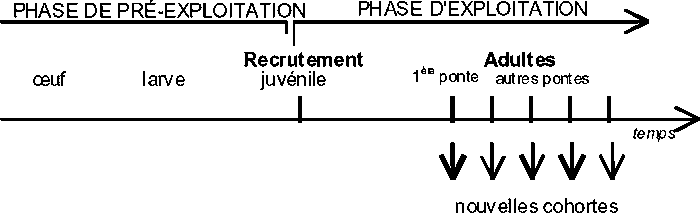
On commence, par exemple, par la phase de l’œuf. Les phases suivantes seront larve, juvénile et adulte.

On désigne par recrutement à la pêche ou à la phase d’exploitation le nombre d’individus d’une cohorte qui entre pour la première fois dans la zone de pêche. Ces individus grandissent, pondent (une ou plusieurs fois) et meurent.

Dès la 1^ère ponte les individus de la cohorte sont appelés adultes, et, généralement, ils pondent à nouveau tous les ans, donnant ainsi origine à de nouvelles cohortes.

Les phases de la vie de chaque cohorte qui précèdent le recrutement à la zone de pêche (œuf, larve, pré-recrues), sont des phases importantes de leur cycle de vie, mais, généralement, elles ne sont pas sujettes à l’exploitation, les variations d’abondance étant dues essentiellement à la prédation et aux facteurs de l’environnement (vents, courants, température, salinité...). La mortalité dans ces phases de non-exploitation est normalement très élevée surtout pendant la dernière phase larvaire (Cushing, 1996) résultant, ainsi, en une survie très réduite jusqu’au recrutement, cette mortalité, comme indiqué plus haut, n’est pas causée par la pêche.

Le recrutement à la phase d’exploitation d’une cohorte (le nombre d’individus qui entrent pour la première fois dans la phase exploitée dans une année déterminée), peut survenir pendant plusieurs mois sous les formes schématiques suivantes:

Figure 3.2 Recrutement à la phase d’exploitation

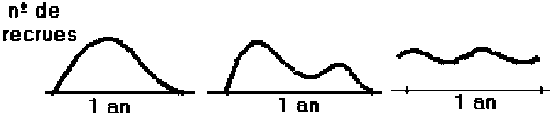
À l'exception de quelques cas, les formes de recrutement peuvent se simplifier si l’on admet que tous les individus recrutent à l’instant, t_r, désigné par âge de recrutement à la phase d’exploitation. Par convention, on considère que le recrutement a lieu le 1^er janvier (début de l’année civile dans plusieurs pays). La simplification et la convention mentionnées antérieurement n’altèrent pas beaucoup les résultats des analyses, mais simplifient ces dernières et correspondent aux périodes auxquelles les statistiques commerciales s’appliquent.

La 1^ère ponte ne se réalise pas au même âge pour tous les individus de la cohorte. La proportion des individus qui pondent pour la 1^ère fois augmente avec l’âge, de zéro à 100%. À partir de l’âge auquel 100% ont pond la 1^ère fois, tous les individus sont adultes. L’histogramme ou la ligne polygonale qui représente ces proportions est nommé ogive de maturation.

Dans quelques cas l’ogive de maturation peut être simplifiée supposant que la 1^ère ponte a lieu à l’âge t_mat dénommé par âge de 1^ère maturation. Cette simplification signifie que les individus d’âge inférieur à t_mat sont considérés juvéniles et que ceux d’âge égal ou supérieur sont considérés adultes.

La Figure 3.3 représente une ogive de maturation en forme d’histogramme ou de courbe.

Figure 3.3 Ogive de maturation

3.2 Évolution en nombre d’une cohorte, dans un intervalle de temps

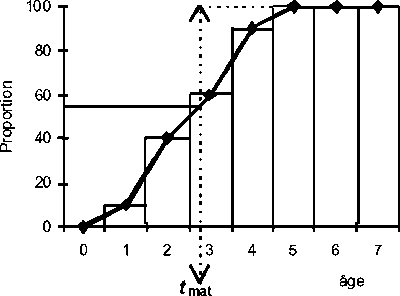
Soit l’intervalle (t_i, t_i+1) de taille T_i = t_i+1 - t_i de l’évolution d’une cohorte avec le temps et N_t le nombre de survivants de la cohorte à l’instant t de l’intervalle T_i (voir Figure 3.4).

L’information existante suggère que les taux moyens de variation en pourcentage de N_t peuvent être considérés à peu près constants, soit, tmr(N_t) » constante.

Supposition de base

Le taux instantané relatif de variation de N_t , dans l’intervalle T_i est:

tir (N_t) = constante négative = - Z_i

Figure 3.4 Évolution de N_i dans l’intervalle T_i

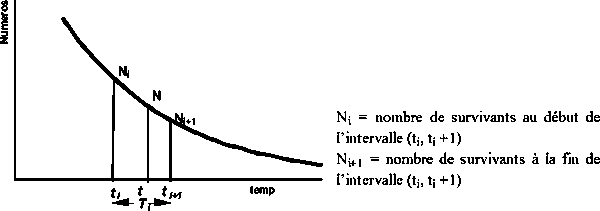
Le modèle de l’évolution de N_t, dans l’intervalle T_i, est un modèle exponentiel (car tir(N_t) est constant). Ce modèle a les propriétés suivantes:

Propriétés

1. Expression générale. De la supposition de base

tir(N_t) = -Z_i

et avec la condition initiale que pour t = t_i on aura N_t = N_i , alors:

2. Nombre de survivants, N_i+1 , à la fin de l’intervalle T_i

3. Nombre de morts, D_i , pendant l’intervalle T_i

(notez que D_i est positif mais la variation DN_i = N_i+1- N_i est négative)

4. Nombre accumulé de survivants, N_cumi , pendant l’intervalle T_i

Valeur centrale rapprochée, N_centrali , dans l’intervalle T_i

6. Nombre moyen, 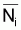, de survivants pendant l’intervalle T_i

(Ricker)

quand est petit (Z_i.T_i < 1)

Commentaires

1. La supposition de base est parfois présentée en termes de taux instantanés absolus, soit,

tia (lnN_t) = -Z_i ou

tia (N_t) = - Z_i.N_t { tia (N_t) proportionnel à N_t}

Z_i = coefficient de mortalité total, supposé constant dans l’intervalle T_i

Notez que:

+Z_i = tir de mortalité total de N_t

-Z_i = tir de variation de N_t

2. Unité de Z_i

De la définition on déduit que Z_i est formulé en unités de [temps]^-1. Par convention on adopte l’unité "an^-1" même s’il s’agit d’un intervalle inférieur ou supérieur à un an.

Les expressions suivantes montrent de façon simplifiée le calcul de l’unité de Z_i, avec les règles et symboles [..] de dimension habituelle dans la détermination d’unités physiques.

3. Taux annuel de survie, S_i

Quand T_i =1 an:

et aussi

S_i = taux annuel de survie en l’an i

(ou % du nombre initial d’individus qui survivent à la fin de l’année).

1 - S_i = taux annuel de mortalité en l’an i

Par définition c’est le % du nombre initial qui meurt pendant l’année.

Soit le taux relatif moyen tmr(N_t) de mortalité de N_t, pendant un an, par rapport au nombre initial, N_i

4. Taux absolut moyen

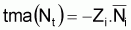
5. Taux relatif moyen 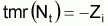relatif à

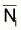
6. Notez que S_i est compris entre 0 et 1, soit,

0 £ S_i £ 1 mais Z_i peut être > 1

7. Si les limites de l’intervalle T_i étaient (t_i, ) alors on aurait:

T_i =

N_i+1 = 0

D_i = N_i

et

3.3 Capture en nombre dans un intervalle de temps

Les causes de mort dues à la pêche seront séparées des autres causes de mort des individus de la cohorte. Ces dernières sont groupées en une cause unique désignée par mortalité naturelle. Ainsi, des propriétés du modèle exponentiel, on aura

tir(N_t) _total = tir(N_t) _naturel + tir(N_t) _pêche

Si l’on considère l’intervalle T_i et en supposant que, dans cet intervalle, les taux instantanés de mortalité par causes naturelles et par pêche sont constants et égaux à M_i et à F_i, respectivement, on aura:

Z_i = F_i + M_i

En multipliant les deux termes de l’égalité précédente par on aura:

comme 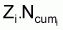est le nombre, D_i , de morts dus à la mortalité totale, alors,

De même 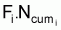sera le nombre d’individus morts par la pêche, soit, la capture, Ci, en nombre et, donc,

Notez aussi que 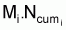sera le nombre d’individus morts par des causes naturelles.

Le taux d’exploitation, E_i , pendant l’intervalle T_i a été défini par Beverton et Holt (1956) comme étant:

et donc, ou encore

La capture en nombre, C_i, dans l’intervalle T_i, peut être formulée sous les différentes formes suivantes:

Commentaires

1. Ricker (1975) définit le taux d’exploitation, E_i*, comme le pourcentage du nombre initial qui est capturé dans l’intervalle T_i, soit, E_i* = C_i / N_i.

a) La définition de Ricker peut être plus naturelle mais mathématiquement la définition de Beverton & Holt est plus utile.

b) Il est facile de vérifier que

2. Le taux d’exploitation, E_i , n’a pas d’unité, c’est un nombre abstrait.

3. Les valeurs possibles de E_i sont comprises entre 0 et 1, 0 représentant l’absence d’exploitation et 1 la capture C_i égale au nombre de morts D_i, soit, M_i = 0.

3.4 Croissance individuelle

Pour étudier l’évolution de la biomasse d’une cohorte, on peut utiliser le modèle de l’évolution d’une cohorte en nombre et la combiner avec un modèle d’évolution du poids moyen d’un individu de la cohorte. En effet, la biomasse B_t est égale à N_t.W_t où W_t est le poids moyen individuel à l’instant t. D’un autre côté, il y a aussi intérêt, plus généralement, de disposer d’un modèle pour l’évolution du poids individuel, W_t, et d’un modèle pour l’évolution de la longueur individuelle, L_t.

Pour définir un modèle pour la croissance en poids individuel, 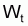, on dispose de plusieurs alternatives.

1^ère ALTERNATIVE:

A) Définir un modèle pour la croissance individuelle moyenne en longueur,

B) Définir la relation Longueur-Poids.

C) Combiner A) avec B) et obtenir un modèle pour la croissance individuelle moyenne en poids,

2^ème ALTERNATIVE:

D) Définir un modèle directement pour et L_t.

1^ère ALTERNATIVE

A) Modèle pour la croissance individuelle en longueur

Les modèles à utiliser en biologie marine sont valides pour la phase d’exploitation de la ressource. Le plus connu est le Modèle de von Bertalanffy (1938). Les observations suggèrent qu’il existe une longueur asymptotique, c’est-à-dire qu’il existe une longueur vers laquelle la longueur individuelle tend.

Figure 3.5 Modèle de von Bertalanffy

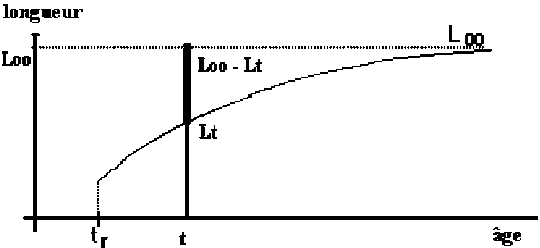
t - âge

L_t - longueur moyenne individuelle à l’âge t

L - longueur asymptotique

t_r - début de la phase d’exploitation

Ainsi, L_t présente une évolution où l’on peut vérifier que:

Le tia(L_t) n’est pas constant (car la croissance n’est pas linéaire)

Le tir(L_t) n’est pas constant (car la croissance n’est pas exponentielle)

On observe, pourtant, que la variation de la quantité 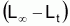(que l’on pourrait appeler “ce qu’il reste à grandir”), présente un taux relatif constant et pourra être décrite par un modèle exponentiel. Ainsi on peut adopter la:

Supposition de base

tir (L - L_t) = - K = constante négative durant toute la vie exploitée

où K est le coefficient de croissance (attention: le coefficient de croissance K n’est pas la vitesse de croissance mais la vitesse relative de ce qu’il “reste” à grandir !!).

Les propriétés de ce modèle (puisqu’il s’agit d’un modèle exponentiel) peuvent être obtenues directement à partir des propriétés générales du modèle exponentiel avec la condition initiale:

Propriétés du modèle de croissance individuelle en taille de Beverton & Holt (1957) déduites du modèle exponentiel de (L-L_t).

B) Relation Longueur-Poids

Il est commun d’utiliser la fonction puissance pour mettre en rapport le poids individuel avec la longueur totale (ou autre). Ainsi:

où la constante a est désignée par facteur de condition ou indice pondéral et la constante b par constante de morphisme. Cette relation peut être justifiée en acceptant grosso-modo que “le pourcentage de croissance en poids” est proportionnel “au pourcentage de croissance en longueur” (dans le cas contraire l’individu serait “disproportionné”) et, en adoptant la supposition basique:

où b est la constante de proportionnalité.

2^ème ALTERNATIVE

D) Modèle directement pour W_t et L_t

Dans la 1^ère alternative, on a développé un modèle pour la croissance en longueur, et ensuite un modèle pour la croissance en poids, en utilisant la relation entre le poids et la longueur.

La supposition de base adoptée par la 1^ère alternative a utilisé la caractéristique 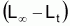au lieu du poids afin d’avoir une caractéristique où tir est constant, c’est-à-dire un modèle exponentiel, et considérer la relation W=a.L^b pour dériver le modèle de croissance en poids. Notez que l’on peut dire que L a été considéré comme étant fonction de W, soit, L=(W/a)^1/b. Il sera, donc, possible préférer à cette fonction de W, une autre fonction du poids 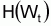, de façon a que l’on puisse formuler directement la supposition de base:

avec la condition initiale

Propriétés

Les propriétés de ce modèle (puisqu’il s’agit d’un modèle exponentiel) peuvent êtres obtenues directement a partir des propriétés du modèle exponentiel. Il est particulièrement intéressant de dériver l’expression générale pour 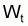résultante de différents choix de la fonction H.

Commentaires

1. L’équation de Gompertz, en poids est semblable à l’équation de Gompertz, en longueur, mais dans ces formes simplifiées t* sont des âges différents, puisqu’ils correspondent respectivement à W_a = 1 et à L_a = 1.

2. L’équation de Gompertz en longueur est semblable à celle de von Bertalanffy avec L_t substitué par lnL_t. Dans les cas pratiques cela permet l’utilisation des mêmes méthodes particulières d’estimation des paramètres dans les deux équations, utilisant L dans l’expression de von Bertalanffy et lnL dans l’expression de Gompertz. (voir Section 7.4)

3. On rappelle à nouveau que, dans la pratique, on utilise L_centrali et W_centrali au lieu des valeurs moyennes, 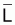et

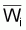
4. La courbe de croissance en longueur de Gompertz infléchit au point (t_infl, L_infl) avec:

t_infl = t_a+(1/K).ln(ln(L/L_a)) L_infl = L / e

5. La courbe de croissance en poids de Gompertz infléchit au point (t_infl, W_infl) avec:

t_infl = t_a+(1/K).ln(ln(W/W_a)) W_infl = W / e

6. La courbe de croissance en longueur de Richards n’a pas de point d’inflexion mais la courbe de croissance en poids a une inflexion au point (t_infl, W_infl):

Dans le cas particulier de l’équation de von Bertalanffy sera:

W_infl = (8/27).W et t_infl = t₀+(1/k).ln3

7. Quelques auteurs se réfèrent à l’équation de Gompertz sous d’autres formes, en utilisant comme paramètres t_a et W_a le point d’inflexion t_infl et le poids asymptotique W.

Donc, on aura

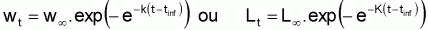
Parfois l’expression est présentée dans sa forme générale

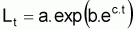
Les paramètres du modèle seront L = a; k = -c et t_infl = (1/c).ln(-b)

8. En aquaculture, où l’étude de la croissance comprend des âges très tendres et où une inflexion dans la croissance en longueur est vérifiée, on a l’habitude d’utiliser l’équation de Gompertz. Dans la pêche on utilise traditionnellement l’équation de von Bertalanffy.

9. Un modèle, qui peut s’avérer utile, est celui de Ricker (1975). Ce modèle est valide pour un intervalle de temps T_i donné et non pas seulement pour toute la vie exploitée de la ressource. En effet le modèle est basé sur la supposition basique que la croissance individuelle est exponentielle dans l’intervalle T_i.

Il en sera ainsi, par exemple dans 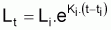où K_i peut différer d’intervalle en intervalle.

3.5 Biomasse et capture en poids, dans l’intervalle T_i

1. Biomasses

Théoriquement, on pourrait dire que la biomasse à l’instant t de l’intervalle T_i est donnée par:

B_t = N_t. W_t

et, donc, la biomasse accumulée dans l’intervalle T_i serait:

et la biomasse moyenne dans l’intervalle T_i serait:

Le poids moyen de la cohorte, 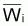, dans l’intervalle T_i serait:

Et, en divisant les deux termes de la fraction par T_i sera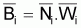

2. Capture, en poids

La capture en poids, Y_i , pendant l’intervalle T sera exprimée comme le produit de la capture, C_i , fois le poids moyen individuel pendant l’intervalle T_i:

Commentaires

Dans la pratique 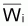est considéré à peu près égal à dans l’intervalle T_i.

L’expression antérieure de Y_i peut aussi être formulée comme:

3.6 Cohorte pendant toute la vie exploitable

On considère l’évolution d’une cohorte pendant toute la vie exploitable, débutant à l’âge t_r. On considère des intervalles, T_i, de temps, où i varie du premier au dernier intervalle, couvrant toute la phase d’exploitation (fréquemment les intervalles sont d’un an...).

La Figure 3.6 simule l’évolution du nombre de survivants de la cohorte, N , et l’évolution des captures en nombre, C, qui sont obtenues pendant les successifs intervalles de temps T_i.

Figure 3.6 Évolution du nombre de survivants de la cohorte, N, et des captures en nombre, C

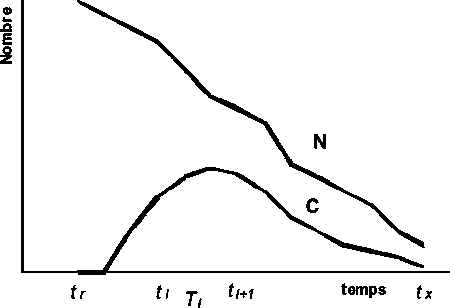
La Figure 3.7 simule l’évolution de la biomasse de la cohorte, B, et l’évolution des captures en poids, Y, qui sont obtenues pendant les intervalles de temps successifs T_i.

Figure 3.7 Évolution de la biomasse de la cohorte, B, et des captures en poids, Y

Valeurs des caractéristiques plus importantes de la cohorte, pendant toute la phase d’exploitation

Commentaires

1. À première vue, il semblerait que les valeurs des caractéristiques d’une cohorte pendant toute la phase d’exploitation ne présentent pas grand intérêt, car, dans la pratique, la pêche s’exerce rarement sur une cohorte isolée. À chaque instant, les survivants de plusieurs cohortes sont présents et disponibles à la pêche simultanément.

2. Malgré cela et pour des raisons que l’on verra plus tard, il importe d’analyser les caractéristiques d’une cohorte pendant toute sa vie exploitable. La connaissance de l’évolution d’une cohorte, en nombre et en biomasse, particulièrement l’âge critique, a une grande importance pour le succès des activités de l’aquaculture. Comme B_t = N_t. W_t l’âge critique, t_{critique ,} sera l’âge t dans l’intervalle T_i où tir (W_t) = - tir(N_t)=M car étant l’âge critique correspondant à la biomasse maximale non exploitée, la dérivée de B à l’ordre de t sera égale à zéro.

3. Notez que N_cum peut être exprimé en fonction du recrutement comme

N_cum = R.{...}

où {...} représente une fonction des paramètres biologiques et des coefficients de mortalité F_i pendant les années de la vie de la cohorte. B_cum peut aussi être exprimé comme:

B_cum = R.{...}

où {...} a le même sens et inclut les paramètres de croissance.

3.7 Simplification de Beverton et Holt

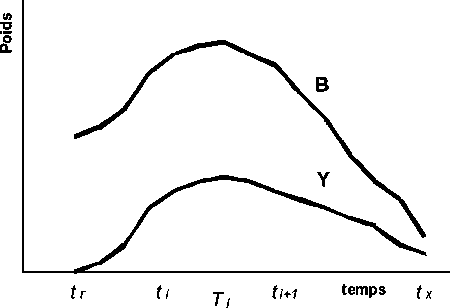
Beverton et Holt (1957) ont déduit des expressions algébriques pour les caractéristiques d’une cohorte pendant la vie exploitée en adoptant quelques suppositions simples:

1. La phase exploitée de la cohorte débute à l’âge t_c et s’étend jusqu’à l’infini.

2. Le coefficient de mortalité naturelle, M, est constant pendant toute la phase d’exploitation.

Figure 3.8 Vie d’une cohorte pendant la phase d’exploitation

3. Le coefficient de mortalité par pêche, F, est constant pendant toute la phase exploitée, soit, la phase de la vie de la cohorte qui débute à t_c

4. La croissance suit l’équation de von Bertalanffy avec L_a = 0 pour t_a = t₀

Équations de base relatives à la phase d’exploitation

Commentaires

1. La simplification de Beverton et Holt permet le calcul de quelques caractéristiques de la cohorte pendant sa vie avec des expressions algébriques n’étant pas nécessaire la somme des valeurs de la caractéristique dans les successifs intervalles T_i. Ce facteur est utile quand on ne dispose pas d’ordinateur, et c'est pour cela que la simplification a été très utilisée pour effectuer des calculs dans les années 60-70. Elle est aussi utile quand on dispose seulement, pour l’évaluation des ressources, de données de mortalité naturelle, M, et de paramètres de croissance.

2. La simplification est aussi beaucoup utilisée actuellement pour étudier les effets des changements dans le coefficient de mortalité par pêche, F, et aussi des changements de l’âge de première capture, t_c , sur la biomasse de la cohorte pendant toute la vie exploitée, sur la capture en poids correspondante et sur le poids moyen à la capture. Ces analyses sont normalement illustrées par des figures. Par exemple la Figure 3.9 illustre l’analyse des biomasses et des captures en poids obtenues d’une cohorte pendant la vie exploitée, sujette à différents coefficients de mortalité par pêche supposant un âge t_c fixe.

Figure 3.9 Évolution des biomasses et des captures en poids d’une cohorte sujette à différents coefficients de mortalité par pêche et t_c fixe (notez que la Figure illustre seulement l’analyse et ne prends pas en compte les échelles des axes).

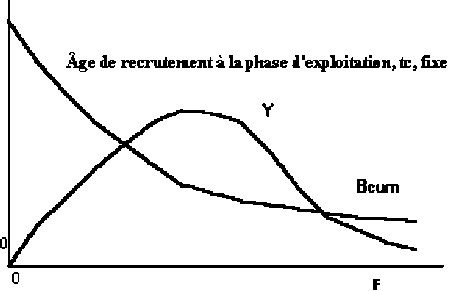
3. Notez que les formes des courbes antérieures, Y et B_cum contre F, ne dépendent pas de la valeur du recrutement et, sont communément désignées par courbes de biomasse et capture par recrue, B/R et Y/R, respectivement. Pour simplifier les calculs sont réalisés en admettant R=1000.

4. De toutes les caractéristiques de la cohorte pendant la vie, le poids moyen à la capture (ainsi comme l’âge et la longueur moyens à la capture) ne dépendent pas de la valeur du recrutement. Ces courbes des caractéristiques d’une cohorte pendant la vie contre le niveau de pêche, F, ou contre l’âge de la 1^ère capture, t_c, méritent une étude plus soignée pour des raisons exposées dans le chapitre sur les prévisions du stock à long terme.

5. B_cum a été calculé comme:

où

Les calculs peuvent aussi être réalisés en utilisant une valeur de la constante b, de la relation W-L, différente du coefficient d’isomorphisme, b=3.

Pour cela, on peut recourir à la fonction mathématique Beta incomplète (Jones, 1957).

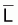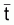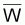6. Pour le calcul de et on procède de mode identique au calcul de , soit, on calcule

Ces moyennes sont désignées par moyennes pondérées, étant les facteurs de pondération le nombre de survivants N_t à chaque âge t.