7. Calculs relatifs aux cales et aux conteneurs à poisson isothermes - quelques exemples

Plusieurs exemples des calculs de base concernant les cales et les conteneurs à poisson isothermes sont présentés dans ce chapitre. Une section est consacrée au calcul de la glace nécessaire pour la réfrigération du poisson frais, tandis qu'une autre section traite de la détermination du volume des cales à poisson.

7.1 Calcul du taux de fusion spécifique de la glace dans une cale ou un conteneur à poisson isotherme

Plusieurs méthodes permettent de calculer le taux de fusion de la glace dans un conteneur isotherme, notamment:

a) les méthodes mathématiques et numériques;
b) des méthodes empiriques basées sur des tests de fusion de la glace.

Les méthodes mathématiques et numériques permettent de calculer le taux de fusion de la glace dans les conteneurs à partir du coefficient de conduction (U), de la surface à travers laquelle s'opère le transfert thermique (A) et de la chaleur latente de fusion de la glace (L), qui est de 80 kcal/kg pour l'eau douce et de 77,8 kcal/kg pour l'eau de mer. Pour calculer le taux de fusion de la glace dans un conteneur donné (K¹), exprimé en kilos de glace/h °C, on applique l'équation suivante:

Le coefficient de conduction (U) (kcal m^-2 h^-1 °C^-1) correspond au taux de pénétration de la chaleur à travers les parois du conteneur par m² de surface et par degré centigrade d'écart de température entre l'intérieur et extérieur. Cette valeur dépend du coefficient de conductance thermique des matériaux composant la paroi du conteneur (l), de leur épaisseur et de la vitesse à laquelle la chaleur passe du milieu ambiant à la cloison extérieure du conteneur, puis de la paroi intérieure au contenu (par exemple le mélange de poisson et de glace).

Pour un conteneur isotherme composé de couches de matériaux différents, le coefficient de conduction peut être calculé par l'équation suivante:

Si:

a1 = coefficient de conduction à l'extérieur de la paroi du conteneur
a2 = coefficient de conduction à l'intérieur de la paroi
di = épaisseur des couches de matériaux composant la paroi
l = coefficient de conductance thermique des matériaux composant la paroi
j = coefficient permettant de tenir compte de l'influence des nervures de renfort sur la structure du bateau et du montage de soutien de la paroi isotherme (membrures, barrots de pont, éléments divers, etc., susceptibles de créer des ponts thermiques).

Pour plus de simplicité, on omet parfois les coefficients a1 et a2 qui influent relativement peu sur le résultat. Toutes ces méthodes exigent cependant de solides connaissances de la transmission thermique, des moyens de laboratoire, des logiciels et du matériel informatique qui ne sont généralement pas disponibles dans le secteur de la pêche artisanale.

L'apport de chaleur à travers un élément donné peut être calculé par l'équation suivante:

Si:

Q = taux global de transfert thermique à travers l'élément (kcal/h)
A = surface de l'élément (m²)
U = coefficient de transfert thermique pour l'élément considéré (kcal m^-2 h^-1 °C^-1)
t_o = température à l'extérieur de l'élément (°C)
t_i = température à l'intérieur de l'élément (°C)

Exemple: Les calculs ci-dessous portent sur un bateau en acier équipé d'une cale ou de réservoirs d'EMRG. Pour calculer le taux de transmission thermique (valeur U) de la cale, il faut connaître les coefficients de transfert de chaleur de tous les éléments entrant en ligne de compte. La relation suivante est calculée à partir de l'équation 1.

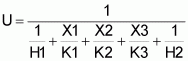
Si:

H1 = coefficient de transfert de chaleur extérieur (kcal h^-1 m^-2 °C^-1)
H2 = coefficient de transfert de chaleur intérieur (kcal h^-1 m^-2 °C^-1)
K1 = conductivité thermique des panneaux d'acier sur les flancs du bateau (kcal h^-1 m^-1 °C^-1)
K2 = conductivité thermique du polyuréthane (kcal h^-1 m^-1 °C^-1)
K3 = conductivité thermique des panneaux d'acier garnissant le réservoir (kcal h^-1 m^-1 °C^-1)
X1 = épaisseur des panneaux d'acier sur les flancs du bateau (m)
X2 = épaisseur du polyuréthane (m)
X3 = épaisseur du revêtement de la cale (m)

Une fois que l'on a calculé les coefficients de transmission de chaleur pour chacun des éléments de la cale (vaigrage de plafond, fond de cale, cloison de la salle des machines, cloison avant, flancs du bateau au-dessus et au-dessous de la ligne de flottaison), on peut calculer les apports calorifiques à travers chaque surface au moyen de l'équation 3. Il faut calculer la surface de chaque élément ainsi que la température type des panneaux intérieurs et extérieurs.

Le taux d'échange thermique global pour l'ensemble de la cale ou du conteneur à poisson est la somme des différents calculs de la valeur Q. Le Tableau 7.1 indique les apports de chaleur calculés (kcal h^-1 m^-2) pour un bateau à coque acier équipé d'un réservoir d'EMRG en acier, avec une isolation de polyuréthane de 100 mm d'épaisseur, et sans isolation. Ces calculs se rapportent à des conditions idéales (sans membrures ou supports traversant l'isolant, et donc sans pont thermique). Sur un bateau de pêche, c'est principalement par le vaigrage de plafond et les flancs du bateau, au-dessus et au-dessous de la ligne de flottaison, que la chaleur pénètre dans les réservoirs d'EMRG non isolés, avec des coefficients globaux d'échange thermique de 27,6, 27,6 et 374 kcal m^-2 h^-1 °C^-1. Pour d'autres parties du bateau, comme la cloison de la salle des machines et le plancher du réservoir, ces coefficients sont de 7,03 et 7,73 kcal m^-2 h^-1 °C^-1. Toutefois, on a calculé que le coefficient total de transfert de chaleur pour un réservoir d'EMRG parfaitement isolé thermiquement est en moyenne de seulement 0,21 kcal m^-2 h^-1 °C^-1 (dans des conditions idéales). Le Tableau 7.1 donne également les écarts de température entre la surface intérieure du réservoir d'EMRG (0 °C) et d'autres parties du bateau, ainsi que les infiltrations de chaleur.

Etant donné qu'un kilo de glace absorbe 80 kcal en fondant, il faudra prévoir au total 7,7 kg/h de glace (soit 185 kg/jour) pour compenser les apports de chaleur dans le réservoir d'EMRG isolé que nous avons pris comme exemple. En conséquence, pour une sortie de pêche de quatre jours, il faudra 740 kg pour compenser les entrées de chaleur par les parois. Dans la pratique, on peut toutefois estimer que les ponts thermiques dans des réservoirs d'EMRG de même type isolés conformément aux normes commerciales (et donc partiellement seulement), sont en fait de l'ordre de 7 pour cent de l'apport total de chaleur.

Une méthode simple et pratique de calcul du taux de fusion de la glace dans un conteneur (K^exp) qui reposant sur des données relatives à la masse de glace fondue en une période donnée, a été mise au point pour les bateaux de pêche artisanale et jugée bien adaptée. Il est fondé sur l'hypothèse selon laquelle il existe une relation linéaire entre le taux de fusion de la glace dans un container et le temps écoulé, à température ambiante constante. Dans la pratique cependant, le taux de fusion de la glace dans les conteneurs varie selon qu'ils sont stockés à l'ombre ou au soleil.

TABLEAU 7.1
Apports calorifiques dans le réservoir d'EMRG en acier d'un bateau de pêche à coque acier

Note: épaisseur des plaques d'acier doux: flancs du bateau: 6 mm; revêtement du réservoir d'EMRG: 5 mm.
Source: FAO, 1992b.

Le taux de fusion spécifique de la glace (K¹) peut être calculé au moyen de l'équation suivante:

Si:

M_i (t) = masse de glace à l'intérieur du conteneur au moment t (kg)
M_i (0) = masse initiale de glace à l'intérieur du conteneur au moment t = 0 (kg)
K¹ = taux de fusion spécifique du conteneur (kg de glace/h °C)
T_{e (a)} = température moyenne à l'extérieur du conteneur (°C)
t = temps écoulé depuis le début du glaçage dans le conteneur (h)

Cette méthodologie décrite par Lupin (FAO, 1986) se décompose en trois étapes:

1. Déterminer les caractéristiques techniques du conteneur isotherme testé.

2. Procéder à une pesée précise du conteneur (vide et sec).

3. Remplir complètement le conteneur de glace et procéder à une nouvelle pesée.

4. Enregistrer l'heure où le conteneur isotherme a été rempli de glace ainsi que le poids de la glace chargée (calculé par la différence de poids).

5. Mettre le conteneur à l'ombre, et enregistrer précisément les conditions de travail du moment.

6. Relever la température ambiante à intervalles réguliers afin de calculer une moyenne. De jour, il est recommandé de relever la température toutes les heures (pour des essais courts de six à huit heures); la nuit, on utilisera un thermomètre à maxima et minima pour enregistrer les données d'expérimentation. Si on peut y avoir accès, on peut obtenir des résultats plus précis avec des enregistreurs de température-temps.

7. Si le conteneur permet le drainage de l'eau de fusion, la perte de poids peut être relevée régulièrement (par exemple toutes les heures) pour mesurer précisément le taux de fusion de la masse de glace dans le conteneur.

8. Ce test de fusion ne doit être réalisé qu'avec de la glace bien que la méthode reste valide pour le mélange glace/poisson (à condition de tenir compte de la glace utilisée pour réfrigérer le poisson). Par ailleurs, une partie de la fusion initiale sera due à la chaleur absorbée pour réfrigérer le conteneur et en fonction du type de matériau, une partie de l'eau de fusion pourra aussi être absorbée par le conteneur lui-même.

9. Les données relatives à la masse de glace fondue (perte de poids) sont reportées sur un graphique en fonction du temps. On devrait obtenir une ligne plus ou moins droite (tout dépendra en fait des variations de la température extérieure).

La Figure 7.1 illustre des données expérimentales types concernant la fusion de la glace en fonction du temps pour un conteneur isotherme de 90 litres entreposé à l'ombre. Le taux de fusion spécifique de la glace (K^exp) représente la valeur de la pente de la ligne obtenue. Dans cet exemple, la pente de la ligne est de 0,1498, donc K^exp = 0,1498 kg de glace/h (3,6 kg de glace/jour) à une température ambiante moyenne de 28 °C.

Pour déterminer le taux spécifique de fusion de la glace (K^exp) pour le même conteneur à différentes températures ambiantes, il faudra effectuer plusieurs essais à la température voulue. Le Tableau 7.2 donne les valeurs expérimentales des taux spécifiques de fusion (K^exp) obtenus lors de tests réalisés à différentes températures ambiantes. On trouvera à la Figure 7.2 le graphique sur lequel est reportée la relation entre les données expérimentales de K^exp, pour le conteneur isotherme décrit à la

TABLEAU 7.2
Valeurs expérimentales des taux spécifiques de fusion de la glace (Kexp) à différentes températures

Note: les données concernent les tests réalisés avec le conteneur isotherme décrit à la Figure 7.1.

Figure 7.1, à diverses températures ambiantes. Les résultats de la Figure 7.2 peuvent être exprimés par l'équation de la ligne droite obtenue y = 0,1233x et ajustés comme suit:

L'exemple suivant illustre l'application des résultats obtenus à la Figure 7.2.

Exemple: Déterminer la quantité de glace consommée dans le conteneur isotherme décrit à la Figure 7.1 entreposé à l'ombre pendant une sortie de pêche de cinq jours, à une température ambiante moyenne de 40 °C (sans tenir compte de la quantité de glace nécessaire pour réfrigérer le poisson).

A partir de l'équation 5, le taux spécifique de fusion de la glace peut être calculé comme suit:

K^exp (kg de glace/jour) = 0,1233 T_{e (a)}

K^exp = 0,1233 × 40 °C = 4,932 kg/jour

Le poids total de glace consommé dans le conteneur isotherme pour compenser les infiltrations de chaleur sera donc: 4,932 kg/jour × 5 jours = 24,660 kg, soit environ 25 kg de glace.

Dans la pratique, il est plus simple d'utiliser directement la Figure 7.2. Le diagramme montre qu'à une température ambiante de 40 °C, environ 5 kg de glace seraient consommés par jour, soit 25 kg en cinq jours.

Note: Il faut utiliser avec prudence les données relatives aux tests ci-dessus. Si les conditions de travail ne permettent pas de protéger les conteneurs du soleil ou de toute autre source de chaleur par rayonnement, les taux de fusion de la glace calculés dans ces tests devront être revus à la hausse. Dans la pratique, il est donc préférable de stocker les conteneurs à l'ombre et, si possible, de les recouvrir (par exemple d'une couverture isolante ou d'une bâche) pour minimiser l'impact des rayonnements de chaleur.

7.2 Méthodologie de calcul de la glace nécessaire pour réfrigérer le poisson frais

En règle générale, on peut calculer le volume total de glace nécessaire pour amener le poisson frais de la température de départ à la température voulue (dans l'idéal 0 °C) par l'équation suivante:

Si:

M_i = masse de glace en fusion (kg)
L = chaleur latente de fusion de la glace (80 kcal/kg)
M_f = masse de poisson à réfrigérer (kg)
Cp_f = chaleur spécifique du poisson frais (kcal/kg °C)
T_fi = température initiale du poisson frais (°C)
T_fo = température finale du poisson frais (°C), généralement 0 °C

Sur la base de l'équation 6, le volume de glace nécessaire pour amener le poisson à 0 °C sera:

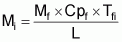
La chaleur spécifique du poisson varie selon sa composition chimique; pour un poisson à chair maigre, cette valeur sera de l'ordre de 0,8 (kcal/kg °C), tandis que pour un poisson gras, elle se situera environ à 0,75 (kcal/kg °C). Pour plus de facilité, on peut utiliser la valeur de 0,8 (kcal/kg °C) dans tous les calculs concernant le poisson frais. On obtient ainsi l'équation simplifiée suivante:

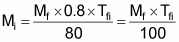
Exemple: Déterminer la glace nécessaire pour réfrigérer 40 kg de poisson frais à partir d'une température de 40 °C.

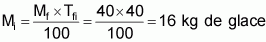
TABLEAU 7.3
Résumé du volume de glace nécessaire pour réfrigérer du poisson frais dans un conteneur isotherme de 90 litres

Note: toutes les valeurs se rapportent aux exemples présentés plus haut..

La Figure 7.3 illustre d'une autre manière la relation entre la température initiale et la glace nécessaire pour amener un kilo de poisson à 0 °C. Le graphique montre que dans ce cas, il faudra environ 0,45 kg de glace pour chaque kilo de poisson. Il faudra donc 18 kg de glace pour 40 kg de poisson.

Dans les tropiques, il faudra toutefois beaucoup plus de glace pour compenser les pertes de capacité réfrigérante due à la fusion de la glace pendant son stockage à température ambiante. Quand la glace est stockée à 27 °C, on a en effet constaté la présence d'une certaine quantité d'eau à la surface des écailles de glace qui représente environ 12 à 16 pour cent du poids total dans des conditions stables. Pour les blocs de glace broyés, l'eau de surface peut représenter 10 à 14 pour cent du poids total. La quantité d'eau en équilibre sur les particules de glace dépendra du type de glace et de la température de stockage.

De mauvaises procédures de manutention pendant la réfrigération et le stockage du poisson peuvent aussi être à l'origine d'un gaspillage supplémentaire de glace, notamment lors du glaçage. On estime que ces pertes représentent 3 à 5 pour cent du poids total de glace utilisé.

Le Tableau 7.3 précise le volume total de glace nécessaire pour amener 40 kg de poisson d'une température de 40 °C à 0 °C et le garder réfrigéré pendant cinq jours dans un conteneur isotherme d'une capacité de 90 litres. On constatera que les 50 kg mentionnés ici représentent un volume légèrement supérieur au minimum empirique d'un kilo de glace pour un kilo de poisson.

7.3 Calcul du volume brut de la cale à poisson

Il est utile de connaître le volume de la cale à poisson, notamment pour la rééquiper ou améliorer son isolation, car on pourra ainsi calculer le volume perdu du fait de la pose des isolants. Cela permet aussi de calculer le volume de glace et du mélange glace/poisson que la cale pourra contenir et donc, de définir des projections optimales pour la longueur des sorties de pêche et le volume des captures.

Quelques méthodes simples permettant de calculer le volume de la cale à poisson avec un degré de précision acceptable sont présentées ci-dessous.

7.3.1 Méthode de l'indice volumétrique

Le Département des pêches de la FAO a élaboré une méthode relativement précise, fondée sur plus de 30 ans d'expérience de la conception et de l'exploitation des bateaux de pêche, pour déterminer simplement le volume des cales à poisson à partir de l'indice volumétrique de bateaux de forme normale. Cette méthode repose sur une série de trois mesures relevées sur le bateau considéré. L'indice volumétrique est calculé comme suit:

LHT × L × Dm

Si:

LHT = Longueur hors tout
L = largeur à mi-longueur au niveau du pont
Dm = distance du pont à la quille à mi-longueur (trait de râblure)

La Figure 7.4 montre où et comment il faut relever ces mesures.

La Figure 7.5 montre comment l'indice volumétrique obtenu à partir des mesures du bateau permet de calculer le volume approximatif de la cale à poisson. Ces chiffres sont généralement fiables à 10 pour cent près.

Comme on peut le voir à la Figure 7.5, le volume de la cale correspond à l'indice volumétrique × 0,14 ± 10 pour cent. Ainsi, un indice volumétrique de 150 m³ correspondrait à une cale d'environ 20 m³.

7.3.2 Méthode des trapèzes

Quand on veut utiliser des mesures directes pour calculer le volume d'une cale à poisson, un calcul relativement facile peut être effectué à l'aide d'une formule simple appliquée aux mesures relevées. Il s'agit de la méthode des trapèzes que l'on emploie sur le terrain du fait de sa simplicité relative, et que l'on considère suffisamment précise dans ces conditions. On peut aussi avoir recours à la méthode de Simpson qui offre une précision légèrement supérieure, bien que de quelques points de pourcentage seulement. Cette méthode exige cependant un nombre pair de divisions et un peu plus de calcul, d'où une augmentation du risque d'erreurs fortuites.

Pour mieux comprendre la terminologie utilisée dans ces calculs, on se reportera à la Figure 7.6 qui illustre les différents termes utilisés dans les calculs ci-dessous.

Pour cet exemple, on trouvera aux Figures 7.7 a) et b) des indications sur l'endroit où prendre les mesures nécessaires et la façon de procéder. On n'utilise ici que trois mesures longitudinales (sections), la première sur la cloison avant, la seconde au centre de la cale et la dernière à la cloison arrière. Pour plus de précision, il suffit d'augmenter le nombre de divisions longitudinales en conservant un écart égal entre elles. En général, la cale est située dans la partie la plus ventrue de la coque volume; le plancher est souvent plat dans la zone proche de l'axe longitudinal et il remonte vers la cloison arrière; les côtés sont plus ou moins parallèles à l'avant et à l'arrière. Sur les bateaux où la cale est située à l'avant de la salle des machines, le plancher est généralement plat. Dans la plupart des cas, trois sections devraient suffire; ce n'est que quand la cale à une forme radicalement différente qu'il faudra relever davantage de sections pour calculer son volume.

La méthode des trapèzes exige des ordonnées régulièrement espacées; on peut en avoir un nombre pair ou impair, mais il est impératif que les mesures soient régulièrement espacées. La première et la dernière des mesures sont divisées par deux; on fait ensuite la somme de tous les chiffres que l'on multiplie par l'intervalle commun correspondant à l'écart entre les mesures. On peut calculer la surface de la section en utilisant les mesures données à la Figure 7.8. Signalons que la surface obtenue doit être multipliée par deux puisqu'elle correspond à la moitié seulement de la section totale.

Dans ce cas, l'intervalle entre les ordonnées correspond à une unité de mesure. On peut utiliser le système impérial ou le système métrique selon les préférences et les habitudes.

Les différentes surfaces de section doivent être ajoutées pour calculer le volume total. Dans ce cas, on calculera de la même manière la surface des zones situées à l'avant et à l'arrière des cloisons de la cale afin d'obtenir la surface totale des trois zones.

On trouvera ci-dessous un exemple des calculs de surface fondés sur les mesures illustrées à la Figure 7.8.

La surface des trois sections permet ensuite de calculer le volume de la cale. Il suffit d'ajouter ces trois surfaces, de diviser le total par trois - ce qui correspond au nombre de sections - pour obtenir la moyenne des surfaces. Le diviseur sera modifié en fonction du nombre de sections. Le nombre d'unités obtenues² est alors multiplié par la longueur de la cale pour en connaître le volume.

Surface à l'avant de la cloison avant = 43,9
Surface du maître-bau = 37,6
Surface à l'arrière de la cloison arrière = 21,1

Volume de la cale = 513 unités³

Pour obtenir un résultat plus précis, il suffit d'augmenter le nombre de sections transversales mesurées dans la cale. Pour la plupart des applications concernant les bateaux de pêche artisanale, on considère que trois sections donnent un calcul assez précis du volume de la cale.

Cale à poisson, cloison avant

Cale à poisson, maître-bau

Cale à poisson, cloison arrière

7.3.3 Multiplicateur utilisé pour le calcul du volume de la cale

Une autre méthode, moins précise, permet d'estimer le volume de la cale à poisson; elle donne d'assez bons résultats lorsque la cale est de forme normale. Elle consiste à appliquer un multiplicateur au volume obtenu en mesurant la profondeur et la largeur de la cale au centre longitudinale et en les multipliant par sa longueur. Le chiffre obtenu est un carré et non une représentation exacte du volume réel. Il faut ensuite appliquer à ce chiffre le multiplicateur dont la valeur peut aller de 0,70 à 0,95 en fonction de la courbe de la section. Les fonds de cale fortement incurvés exigeront un multiplicateur assez élevé, tandis que l'on choisira un multiplicateur plus faible pour une cale présentant une courbe plus ouverte. Cette formule n'est guère rigoureuse et la personne qui relève les mesures doit exercer son jugement professionnel. A mesure qu'elle se familiarise avec la méthode, elle l'appliquera avec davantage de précision.

A partir des chiffres relatifs au maître-bau dans la méthode des trapèzes illustrée plus haut, on obtient le carré suivant:

Etant donné que le fond de cale des sections utilisées dans cet exemple a une courbe assez ouverte, on a opté pour un multiplicateur de 0,75:

Si on compare ce chiffre (529) avec le résultat du premier calcul (513), on constate une erreur de 3 pour cent de plus. Si l'on applique un multiplicateur de 0,8, l'erreur serait toujours de l'ordre de 10 pour cent, ce qui reste acceptable pour une estimation grossière.

7.4 Diminution du volume de la cale due à l'isolation

On peut avoir à calculer la diminution de volume qui résultera de la pose de matériaux isolants dans la cale. A cet effet, il faut mesurer la surface totale de la cale et la multiplier par l'épaisseur de l'isolant.

Prenons, à titre d'exemple, une cale à poisson d'une surface de 40 m² et d'un volume connu de 14 m³ que l'on va isoler avec de la styromousse de 100 mm. Quelle sera la perte de volume?

Cette perte représente quasiment un tiers du volume initial de la cale. Si la diminution de volume pose réellement problème, il convient d'envisager un meilleur isolant ayant une plus forte valeur R. On emploie alors un matériau plus fin qui a les mêmes propriétés isolantes mais occupe moins d'espace dans la cale. A défaut, on peut simplement utiliser un matériau plus fin, mais il faut alors charger davantage de glace pour compenser les apports de chaleur accrus.

7.5 Diminution du volume de la cale due aux compartiments, aux étagères et/ou aux caisses

L'installation de compartiments et d'étagères dans la cale s'accompagne nécessairement d'une réduction de l'espace de stockage disponible, que l'on peut raisonnablement estimer autour de 10 à 15 pour cent. On considère que les revenus moins importants dus au moindre volume de poisson stocké seront compensés par les prix plus élevés obtenus pour des captures de qualité. Il faut aussi tenir compte des pertes de poids occasionnées par l'écrasement des couches inférieures de poisson si on l'empile sur plus de 60 cm. Ces pertes peuvent représenter jusqu'à 15 pour cent du total.

Il existe nécessairement un point d'équilibre entre l'espace qu'occupent les étagères supplémentaires, le complément de main-d'œuvre requis pour le glaçage du poisson sur des étagères plus nombreuses et l'amélioration de qualité obtenue en entreposant les couches de poisson sur moins de 60 cm, d'une part, et la perte de poids et de qualité résultant de l'écrasement des poissons stockés en vrac, d'autre part.

Le poisson frais mis en caisse sous glace, après saignée et éviscération, conserve une qualité optimale. Il est difficile d'en améliorer la qualité sans engager des dépenses assez importantes pour isoler la cale thermiquement ou l'équiper de réservoirs d'EMRG.

La mise en caisse du poisson exige davantage d'espace que son stockage en vrac sous glace - environ 40 pour cent de plus - mais en règle générale, le gain de qualité et la facilité de débarquement au quai compensent très largement la perte d'espace, au moins sur les bateaux de plus grande taille.