C'est l'un des paramètres de base de la dynamique des populations mais son étude est moins critique que celle de la mortalité dans la mesure où l'obtention des résultats est plus facile et où les modèles analytiques sont plus robustes vis-à-vis des données de croissance qu'ils ne le sont vis-à-vis de la mortalité. Dans le cas le plus général, on étudie la croissance individuelle et on considère que la croissance de la population n'est que l'addition simple de celle de ses composants. Dans le cas des penaeïdes, on se heurte à plusieurs difficultés:
Les crustacés ne portent pas de structure osseuse gardant l'empreinte des variations d'ambiance interne et externe et susceptibles de permettre une lecture directe de l'âge. Notons cependant que selon Yano et Kobayashi (1969), le nombre de lamelles dans l'endocuticule augmente avec la taille offrant une possibilité de lecture de l'âge.
La croissance est discontinue et le phénomène de la mue rend délicates les techniques de marquage et en particulier l'usage des marques externes (disques de Petersen, etc.). Selon Boddeke, Dijkema et Siemelink (1977) cependant, la croissance en longueur continuerait pendant l'intermue par étirement des parties souples de la carapace, la taille des boucliers dorsaux-latéraux étant inchangée. Ils montrent d'ailleurs que le rapport taille des boucliers/longueur totale varie de façon cyclique entre deux mues.
Comme beaucoup d'espèces tropicales, les crevettes penaeïdes ont une reproduction le plus souvent continue, rendant difficile l'utilisation des méthodes de décomposition des courbes de fréquence polymodales.
Les travaux de base sur ce sujet ne manquent pas et l'on se réfèrera, entre autres, à ceux de Kurata (1962) et Mauchline (1977) pour l'étude des mues et de la croissance chez les crustacés, ainsi, d'une façon plus générale, qu'à ceux de Von Bertalanffy (1938, 1964), Walford (1946), Gulland et Holt (1959), Tomlinson et Abramson (1961), Fabens (1965), Southward et Chapman (1965) et Ebert (1973) sans oublier les classiques Beverton et Holt (1956), Gulland (1969), Ricker (1975) et à l'excellente synthèse de Ricker (1979).
Le processus qui permet l'évaluation des paramètres de croissance comprend deux étapes: il faut tout d'abord recueillir les données de base (clés ou couples âge-longueur, accroissements instantanés-longueurs moyennes, etc.) et ensuite résumer éventuellement l'information ainsi réunie en une expression mathématique plus ou moins simple (de type logistique, linéaire, monomoléculaire, etc.). Cette deuxième étape est de plus en plus souvent facultative car l'usage courant des ordinateurs permet d'utiliser les clés âge-longueur observées directement. Elle reste de toute façon approximative car il est rare qu'une seule loi mathématique convienne de la naissance à la mort d'un individu et la simplicité est généralement obtenue au prix d'une approximation. Rappelons également que selon Knight (1968) les paramètres calculés n'ont pas de signification biologique, opinion contestée par Kruger (1969, cité par Ricker, 1979).
5.1.1 La méthode des progressions modales
Cette méthode dont l'origine remonte à Petersen, consiste à suivre dans le temps des modes observés sur des échantillons recueillis périodiquement dans les captures. Chez les penaeïdes, l'âge absolu étant inconnu on définira un âge relatif à partir d'une origine des temps arbitraire (la taille au recrutement, le premier mode observé, etc.). Des données complémentaires sur la phase juvénile permettront éventuellement de recaler la série obtenue sur une date ou une période de naissance si cela apparait necéssaire.
La principale limite de cette méthode réside justement dans la difficulté à identifier chez les penaeïdes côtiers des groupes de taille distincts et à les suivre dans le temps (Fig. 32). Avec un peu d'expérience, on y réussit cependant dans certains cas et les exemples ne manquent pas (Neiva et al., 1971; Galois, 1975; Garcia, 1975; Edwards, 1977). La facilité de l'analyse dépendra du schéma annuel de reproduction et de la qualité de l'échantillonnage.
Dans les zones à forte oscillation saisonnière, on peut souvent suivre la cohorte principale (ou le groupe de cohortes); dans les estuaires, la croissance étant très rapide, un échantillonnage très soigné et avec une fréquence élevée (la semaine), devrait permettre le plus souvent de suivre des micro-cohortes formées grâce au rythme lunaire (de marée) imprimé au recrutement larvaire.
Il est parfois possible de procéder à une décomposition en distributions élémentaires par l'une des nombreuses méthodes plus ou moins sophistiquées disponibles (Harding, 1949; Cassie, 1954; Tanaka, 1956; Battacharya, 1967; Hasselblad, 1966; Gheno et Leguen, 1968; Gregor, 1969). Un certain nombre de programmes disponibles pour ce faire ont été compilés par MacDonald (1969). Seules les méthodes les plus simples ont été utilisées chez les penaeïdes (Cassie et Gheno-Leguen) et les résultats ne sont pas toujours indiscutables au premier abord. Cependant, en Côte d'Ivoire, la croissance de Penaeus notialis calculée à l'aide de la méthode des progressions modales a été vérifiée par marquage (Garcia, 1975).
Le principal défaut de toutes ces méthodes est leur subjectivité évidente ou déguisée. Destinées à l'origine à évaluer les effectifs de classe d'âge graphiquement distincts, elles sont trop souvent utilisées pour subdiviser des courbes de fréquence de taille dont la structure n'apparaît pas. Cette déviation dans l'objectif des méthodes peut conduire à des erreurs graves.
La possibilité d'étudier les crevettes par la méthode des progressions modales, chez des animaux à croissance rapide et à reproduction continue, dépend beaucoup de la maille spatio-temporelle de l'échantillonnage et de la précision des mesures. En particulier, des mesures précises (longueur de la carapace au 1/10e de mm) permettent une séparation plus fine des modes dans les grandes tailles. Les mesures sont le plus souvent effectuées au pied à coulisse ordinaire mais Cole et Mistakidis (1953) et Mauchline (1958) ont proposé des appareils de grande précision, précieux pour la mensuration des petits individus.
L'existence d'une distribution géographique ou bathymétrique hétérogène des tailles et ces sexes est un handicap certain car la reconstitution d'un histogramme représentatif de la population représente un travail délicat. Cet aspect explique la difficulté que l'on rencontre en général lorsqu'on veut analyser des échantillons de la pêche industrielle. Les variations de concentration relative de l'effort sur les diverses strates de la population, liées à des variations de capturabilité, entraînent parfois des changements dans l'aspect des histogrammes d'une marée à l'autre qui ne sont pas liés à la croissance mais résultent du caractère non aléatoire de l'“échantillonnage” réalisé par le bateau de pêche. La difficulté peut alors être tournée si l'on utilise un bateau de recherche avec un plan d'échantillonnage adéquat (échantillonnage stratifié).
Les observations de croissance faites sur des crevettes subadultes en migration (Loesch, 1965; Lhomme, 1979) sont difficiles à interpréter. En effet, dans l'absolu, si la migration des juvéniles vers la mer se faisait à une taille donnée, on observerait des modes fixes et aucune croissance n'apparaîtrait. En revanche, si la migration se produisait à un stade donné du développement (stade de maturation par exemple), la taille à la migration varierait en fonction des conditions de croissance rencontrées dans les diverses parties de l'estuaire et aux différentes saisons. Si enfin la taille à la migration dépendait de la durée du séjour en estuaire, lui-même commandé par les conditions de milieu, elle variererait en fonction des facteurs ambiants, en particulier de la salinité (Garcia, 1977; Le Reste, 1979) ou de la température (Trent, 1967).
Les populations en migration sont en général constituées de nombreuses micro-cohortes 1 et sans un échantillonnage précis permettant de les individualiser, l'assimilation des variations de la taille moyenne à la migration à une croissance peut conduire à des résultats erronés, sous-estimant généralement la croissance réelle. Ce type de données doit donc être considéré avec prudence.
5.1.2 Les marquages
La difficulté que l'on rencontre à identifier des groupes d'âge chez les crevettes peut être résolue par l'utilisation des techniques de marquage. Le principe sera d'individualiser, par une marque visible, un individu ou un groupe d'individus dont on suivra la croissance entre le marquage et la recapture, l'hypothèse de base étant que la marque ne perturbe pas la croissance.
Les injections colorées, correctement utilisées, ne modifient pas le métabolisme (cf. paragraphe 6). Elles permettent de marquer un groupe de tailles isolé par un calibrage. On en suit alors l'évolution de la taille moyenne. Pour couvrir tout l'éventail des tailles présentes dans la population, il est nécessaire de multiplier les marquages avec des injections de couleurs différentes. L'utilisation simultanée de marques secondaires (paragraphe 6.5) augmente sensiblement les combinaisons possibles. Les marques secondaires internes numérotées, en plastique, permettent même de distinguer les individus. C'est également l'avantage des marques externes (disques de Petersen et dérivés) qui autorisent le marquage de toutes les tailles capturées, sans calibrage préalable. Toutes les stratifications sont donc ensuite possibles au moment du traitement des données: séparation par groupes de tailles, par sexe, par état sexuel éventuellement, etc.
Si la technique des injections colorées, bien maîtrisée, est vraisemblablement la plus inoffensive, les marques externes offrent plus de possibilités pour l'interprétation. Les données obtenues par marquage sont: la taille au marquage, la taille à la recapture, donc l'accroissement, et la durée de la période de liberté.
Les recaptures étant assurées par les pêcheurs, les durées de liberté seront extrêmement variables pour un même lot d'individus marqués.
5.1.3 Croissance des mâles
Ils ont en général une croissance plus faible que celle des femelles (un L∞ inférieur et un K supérieur). La conséquence est que les distributions de fréquence, moins étendues sont encore plus difficiles à analyser que celles des femelles parce que plus compactes. Cependant, lorsque la courbe de croissance et la relation taille-âge des femelles est connue, Garcia (1975) à montré que l'on pouvait utiliser une relation entre la taille moyenne des femelles et celle des mâles pour déduire la clé âge-longueur des mâles et leur loi de croissance, de celle des femelles.
Une telle relation est établie en portant la taille moyenne des mâles dans un échantillon (un coup de chalut à une profondeur donnée, par exemple) en fonction de la taille moyenne des femelles dans le même échantillon. La dispersion des points est assez faible et la courbe peut être tracée à main levée. La figure 33 regroupe, la courbe obtenue par Garcia (1975) pour Penaeus notialis et, à titre de comparaison, celle calculée par Iversen et al. (1960) pour P. duorarum.
Si l'on admet que la répartition différentielle moyenne des crevettes sur le fond (Fig. 15), et en particulier les gradients de taille observés, réflètent une répartition liée à l'âge et que les mâles et les femelles capturés ensemble ont, en moyenne le même âge, même si il existe des variations du sex-ratio, on peut passer de la clé longueur-âge des femelles (si on la connait, bien entendu) à celle des mâles, très simplement.
En Côte d'Ivoire cette méthode a donné des résultats identiques à ceux qui ont été obtenus par la méthode de Petersen et par marquage (Garcia, 1975a et b). Lhomme (1978a) a utilisé la même méthode au Sénégal sur la même espèce.
Lorsque les filiations modales “observées” ou supposées pour les mâles, ne sont pas très évidentes, et c'est souvent le cas, cette méthode peut permettre d'éviter des erreurs grossières.
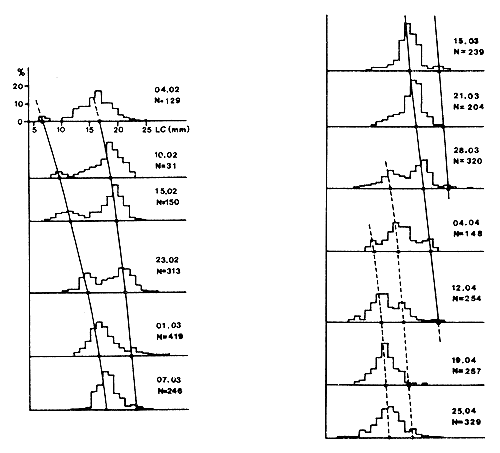
Fig. 32: Croissance de Penaeus notialis en lagune Ebrié (d'après Galois, 1975)
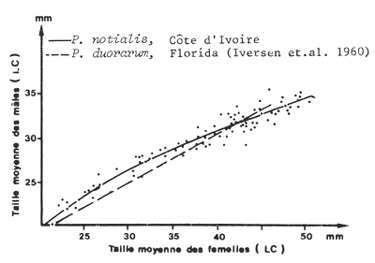
Fig. 33: Relation entre la taille moyenne des femelles et celle des mâles, pour P. notialis (d'après Garcia, 1975) et P. duorarum (repris de Iversen et al., 1960)
5.1.4 Notion d'âge maximum
L'âge des crevettes ne peut être lu directement et les cohortes sont en général difficiles à suivre. Il en résulte que l'âge maximum est difficile à déterminer.
L'analyse des courbes de croissance fournit des valeurs de K plus fortes et de L∞ plus faibles pour les mâles. L'étude de l'évolution du sex-ratio avec la taille (Fig. 30) indique également une dominante nette des femelles au-delà d'une certaine taille. Ces données ont parfois été utilisées chez d'autres espèces marines pour admettre une longévité inférieure pour les mâles (Beverton et Holt, 1959; Holt, 1962).
Une étude, sur deux années complètes, du sex-ratio en fonction de l'âge chez P. notialis en Côte d'Ivoire a pourtant montré qu'il n'y avait pas de tendance nette de ce paramètre avec l'âge et que la longévité des deux sexes devait donc être considérée comme comparable (Fig. 34). Iversen et al. (1960) ont également montré pour P. duorarum que l'on observait aucune tendance lorsque le sex ratio dans différents échantillons était porté en fonction de la taille moyenne des femelles dans ces échantillons. Cette observation conduit également à la conclusion que les durées de vie des mâles et des femelles sont comparables.
A titre indicatif, on trouve rarement des crevettes participant encore significativement aux captures après deux ans d'âge bien que des crevettes âgées d'au moins 27 mois aient été observées par marquage (Baxter, 1971).
Les données de base étant obtenues (couples âge-longueur, accroissements en fonction de la taille), il peut être nécessaire de rechercher l'expression mathématique, le modèle, représentant le mieux la croissance à partir d'une formule simple. La littérature est riche en travaux de base et de synthèse sur ce sujet et il n'est pas nécessaire d'en faire, dans ce travail, une revue exhaustive. Le lecteur se réfèrera plus utilement aux ouvrages de base de Beverton et Holt (1956), Ricker (1958, 1975, 1979), Gulland (1969). Il est rare qu'un seul et même modèle puisse représenter la croissance de façon satisfaisante de la naissance à la mort de l'individu et une approximation doit le plus souvent être acceptée.
Le modèle le plus couramment utilisé est celui de Von Bertalanffy (1938) que Beverton et Holt (1956) ont consacré en l'intégrant dans leurs équations de rendement. D'autres modèles ont été proposés tels que les modèles de Gompertz (Riffenburgh, 1960), logistique (in Ricker, 1971) ou exponentiel (Ricker, 1958). Les propriétés du modèle de Von Bertalanffy ont été examinées par nombre d'auteurs déjà cités ainsi que par Fabens (1965) et Southward et Chapman (1965). Les modèles de Gompertz et Von Bertalanffy ont été comparés par Silliman (1969) et Parrack (1979) en ce qui concerne respectivement les poissons et les crevettes penaeïdes. Leurs résultats prouvent que le modèle de Von Bertalanffy tel qu'on l'utilise actuellement est bien adapté. Des modifications, ou une généralisation, de l'équation de Von Bertalanffy ont été proposées par divers auteurs tels que Richards (1959), Chapman (1961) et Taylor (1962). Bien que leur application aux modèles de Beverton et Holt soit possible (Paulik et Gales, 1964), elles ne semblent pas encore avoir été utilisées. Knight (1969) a également proposé une équation modifiée faisant réellement apparaître le taux de croissance (croissance par unité de temps).
Nous ne nous attarderons pas sur la signification biologique profonde que Von Bertalanffy (1938, 1964) a voulu donner à son modèle et que Ricker (1975), et d'autres (cités par Von Bertalanffy, 1964), ont contesté. Nous retiendrons seulement avec Ricker que le modèle proposé correspond le plus souvent à ce qui est observé et qu'il est donc parfaitement utilisable comme modèle empirique. Cette approche est d'ailleurs conforme à celle de Brody (cité par Ricker, 1975) qui est à l'origine du modèle.
Nous examinerons donc seulement ici le modèle de Von Bertalanffy et passerons très brièvement en revue les méthodes les plus couramment utilisées pour le calcul des paramètres de l'équation. L'expression classique de la courbe de Von Bertalanffy est de la forme:
| lt = L∞ (l-e-K(t-to)) | (5.1) |
où L∞ est la taille moyenne asymptotique vers laquelle tend l'individu. Notons à ce sujet que le principe même de la croissance asymptotique est parfois contesté (Knight, 1968, Ricker, 1979).
K est le coefficient de croissance de Brody (et Ricker (1975) signale qu'il est impropre de parler, pour ce paramètre, de taux de croissance) et to est l'âge théorique des individus lorsque leur taille est nulle. Les méthodes de calcul des paramètres sont nombreuses:
5.2.1 Méthode de Ford-Walford (1946)
Elle est basée sur la forme suivante de l'équation de Von Bertalanffy (Ford, 1933):
| lt+1 = L∞ (1 - k) + klt | (5.2) |
où k, le coefficient de croissance de Ford, est égal à e-K. Walford a montré que la droite d'ajustement de lt+1 sur lt, de pente k, coupait la diagonale à 45° pour lt = L∞ (Fig. 35A). Beverton (1954, cité par Ricker, 1975) propose de ne considérer la valeur de L∞ obtenue que comme provisoire et de porter Loge (L∞ - lt) en fonction de t puisque
| Loge (L∞ - lt) = Loge L∞ + Kto - Kt | (5.3) |
La linéarité de cette relation est sensible à de faibles variations de L∞ et quelques essais de variations de L∞ conduiront à une valeur plus exacte de ce paramètre (Fig. 35B). La pente de la relation (qui dans ce cas est une régression classique si t est connu avec précision) est égale à K et l'ordonnée à l'origine égale à (Loge L∞ + Kto) permet d'obtenir to.
Ricklef (1967) propose également une méthode graphique approximative utilisant une démarche assez voisine pour les courbes de Gompertz, de Von Bertalanffy et logistique en poids. Cette méthode est cependant peu utilisée.
Gulland (1969) montre que to peut également être obtenu graphiquement à partir des mêmes éléments. En effet, d'après l'équation ci-dessus, lorsque lt = 0 (et donc par définition t = to) l'ordonnée est égale à Loge L∞. En conséquence, lorsque l'on porte Loge (L∞ -lt) en fonction de t, le point ayant Loge L∞ pour ordonnée a to pour abscisse (Fig. 36)
L'âge réel est rarement connu. Il est alors possible, soit de considérer que to = 0, soit de prendre pour origine des temps un point remarquable du cycle vital, comme la migration par exemple. L'âge moyen à la migration sera alors pris comme origine (to' = 0) et l'on définira comme dans les paragraphes précédents la courbe de croissance avec un âge relatif t'. Le calcul réel de cet âge moyen à la migration à partir de données sur la ponte et la migration permettra de recaler la courbe sur une échelle des temps réelle.
L'âge à la migration étant susceptible de varier en fonction des conditions ambiantes de l'estuaire, on peut utiliser comme origine des âges relatifs le premier mode observé dans les distributions de fréquence des tailles dans les captures en mer. Cette méthode a été utilisée par Garcia (1970, 1975, 1977) et Galois (1975) sur Penaeus notialis en Côte d'Ivoire, et par Lhomme (1979) au Sénégal, sur la même espèce.
La méthode de Ford-Walford a été adaptée aux données de marquage. Lorsque l'on dispose de données concernant les individus de taille différente ayant été en liberté pendant une période approximativement identique, un graphe de Ford-Walford peut être utilisé en portant la taille individuelle à la recapture en fonction de la taille au largage (Manzer et Taylor, 1947; Hancock, 1965). Cette méthode a été utilisée chez les crevettes penaeïdes par Lindner (1953), Lindner et Anderson (1956), Iversen et Jones (1961), Kutkuhn (1962), Klima (1964, 1974), Berry (1967) et bien d'autres. La procédure est relativement simple. Les recaptures sont regroupées par intervalles de temps égaux, aussi courts que possible (une semaine ou 10 jours). Pour chaque période, on étudie la relation entre la taille à la recapture (Lt + 10 jours) et la taille au marquage (lt). On dispose donc d'autant de courbes de croissance que de périodes élémentaires définies à condition que l'on ait marqué assez de crevettes pour que les recaptures dans chaque période élémentaire soient suffisantes.
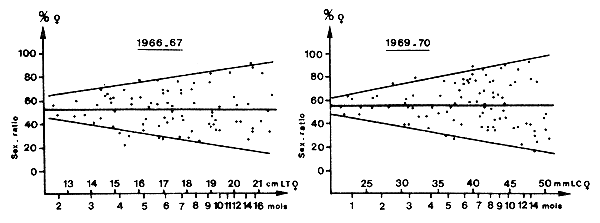
Fig. 34: Variations du sex-ratio en fonction de l'âge ou de la taille des femelles dans les échantillons récoltés en Côte d'Ivoire (d'après Garcia, 1977)
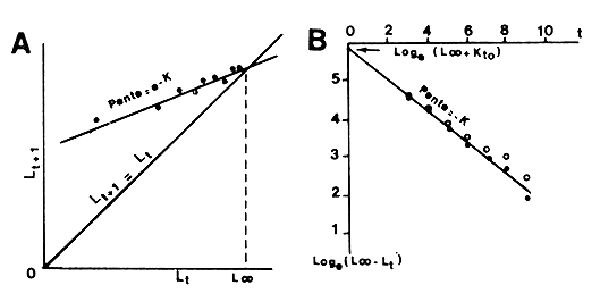
Fig. 35: Calcul des paramètres de la courbe de croissance de von Bertalanffy
A. Méthode de Ford-Walford
B. Méthode de Beverton
(repris de Ricker, 1975)
5.2.2 La méthode de Chapman (1961) (Fig. 37) attribuée à Chapman par Ricker (1979 p. 709), est souvent appelée également méthode de Gulland (1964, 1969). Elle dérive de la forme suivante de l'équation de Von Bertalanffy.
| (lt + 1-lt) = (L∞ -lt) (l - e-K) | (5.4) |
La droite de régression fonctionelle de (lt + l -lt) sur lt est donc une droite de pente - (l - e-K) et d'abscisse à l'origine = L∞. Cette méthode est utilisable pour les marquages. L'accroissement par unité de temps ΔL étant porté en fonction de la taille moyenne au moment du marquage, la croissance est alors calculée en l'absence de toute connaissance de l'âge réel ce qui justifie le terme d'atélique donné par Diaz (1963) à la méthode.
Si les périodes de liberté sont de durée inégale, Gulland et Holt (1959) proposent une méthode de calcul basée sur une correction tangeante hyperbolique. Elle est particulièrement précieuse quand le nombre de recaptures est insuffisant pour permettre un regroupement par strates de liberté de durées égales. La méthode est exposée en détail par Jones (1976). De façon schématique, si (a) est la durée de la période de liberté, (y = (lt + a-lt)/a) l'accroissement par unité de temps et (x) la taille moyenne ((lt + a +lt)/2) pendant la liberté on peut, dans un premier temps, effectuer la régression de y sur x dont la pente donnera une estimation provisoire de K. Si on pose b = Ka/2 les accroissements observés peuvent être corrigés et l'on fera la régression de
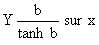
obtenant ainsi une deuxième valeur de K. Le processus est répété jusqu'à stabilisation de la valeur de K. Pour des périodes de liberté courtes (inférieures à 2 mois) la correction n'est pas nécessaire et la valeur de K est stabilisée dès la première étape. Campbell et Phillips (1972) ont proposé une méthode différente pour le même problème mais celle de Gulland et Holt (1959) est préférable quand les intervalles sont importants d'après Ricker (1979).
5.2.3 Discussion sur les méthodes de régression
Ricker (1975 p. 225) précise que le tracé direct d'une régression de lt + 1 en lt n'est pas satisfaisant car les deux variables sont sujettes à erreur, la répartition des points le long de la droite n'est pas normale et tous les points sont utilisés deux fois (comme lt puis comme lt + 1) sauf les deux extrêmes. La modification de Beverton (paragraphe 5.2.1) est destinée à contourner la difficulté. Le problème est le même quand on utilise la méthode des accroissements (paragraphe 5.2.2). Diaz (1963) utilisait une droite fonctionnelle (de Wald, 1940) plus appropriée. Troadec (1968) ainsi que Garcia et al. (1970, 1975) ont utilisé un axe majeur réduit (ou droite de Tessier). Dans son dernier manuel, Ricker (1975) appliquant les résultats de sa réflexion sur l'utilisation des régressions en biologie (Ricker, 1973), préconise l'utilisation de cette dernière méthode et rappelle que Chapman (1961) avait déjà discuté la possibilité d'obtenir les paramètres de l'équation de Von Bertalanffy par régression.
5.2.4 Les méthodes de calcul automatique
L'utilisation de plus en plus courante des ordinateurs permet d'avoir recours à des méthodes de calcul présentant l'avantage de fournir des estimations de la variance des paramètres. En ce qui concerne les données de croissance classiques, le programme VONB de Allen (1966a) permet d'utiliser des données régulièrement ou irrégulièrement espacées dans le temps. Les programmes BGC2 et BGC3 (Abramson, 1971) permettent respectivement d'utiliser des données régulièrement et irrégulièrement espacées.
Le programme CIAT DO5 de Psaropoulos1 applique la méthode de Tomlinson et Abramson (1961). Ce dernier programme a été utilisé par Garcia (1975) sur Penaeus notialis.
1 Il est disponible à l'IATTC, La Jolla, California, U.S.A.
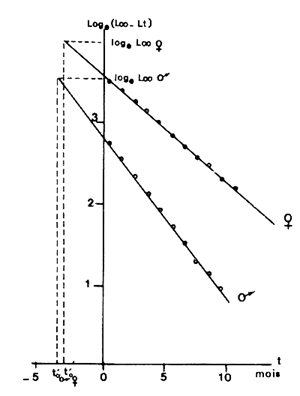 | 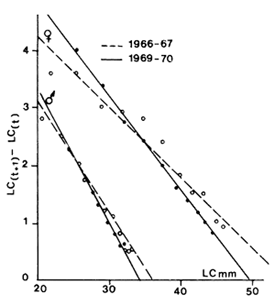 |
Fig. 36: Détermination de t'o par la méthode de Gulland (1969) chez Penaeus notialis. L'origine des âges (t'=0) est arbitraire (voir texte) | Fig. 37: Calcul des paramètres de croissance par la méthode de Chapman (1961) chez Penaeus notialis en Côted'Ivoire |
En ce qui concerne les marquages, Fabens (1965) propose un programme de calcul1 permettant de calculer les paramètres de l'équation de croissance de l'équation originale de Brody par la méthode des moindres carrés. Un exemple d'utilisation sur les crevettes de Madagascar sera trouvé chez Le Reste et Marcille (1976). Ce programme a été modifié par Allen (1967, programme FABVB) et par Tomlinson (in Abramson, 1971, programme BGC4). Southward et Chapman (1965) proposent un programme pour calculer l'équation à 4 paramètres de Richards (1959) par la méthode des moindres carrés.
5.2.5 Les variations saisonnières de croissance
La quantification de ces variations est particulièrement importante pour des animaux à vie courte. Elle peuvent avoir une origine diverse, climatique (Ikematsu, 1955; Lindner et Anderson, 1956; Garcia, 1975, 1977; Lhomme, 1978a; Klima, 1979), (Fig. 38) ou biologique et liée par exemple à la reproduction (Garcia, 1975; Penn, 1975). Lhomme (1978a) a montré une relation entre la valeur de K et la température du milieu, au Sénégal (Fig. 39). Une revue detaillée de ces problèmes sera trouvée dans le récent travail de Ricker (1979).
Lorsqu'elles existent, elles sont de nature à compliquer sérieusement l'analyse de la croissance par la méthode des filiations modales. Elles peuvent être aisément mises en évidence par des marquages répétés à différentes saisons. La conséquence la plus grave de ces variations saisonnières des taux de croissance est que chaque cohorte d'une génération annuelle aura une croissance différente selon sa date de naissance et qu'il n'existera plus de clé âge/longueur unique mais bien autant de clés que de cohortes élémentaires (12 cohortes mensuelles par exemple).
Bien que cette possibilitée n'ait pas encore été utilisée chez les crevettes, rappelons que l'équation de Von Bertalanffy peut être adaptée pour exprimer mathématiquement les variations saisonnières (Lockwood, 1974). D'autre part, Ursin (1963) avait déjà proposé d'incorporer la température dans le modèle de Von Bertalanffy, le temps étant alors exprimé en jours-degrés.
Compte tenu de la difficulté d'analyser les structures de taille des penaeïdes, les marquages apparaissent comme une technique fondamentale pour l'analyse de la croissance et de ses variations saisonnières, malgré les restrictions apportées au chapitre sur les techniques de marquage et leur effet sur le métabolisme.
L'utilisation directe des données observées, dans des modèles de simulation par exemple permettra d'éviter l'utilisation de formules trop complexes et souvent approchées.
La croissance étant étroitement liée aux conditions ambiantes, il sera très important de préciser les conditions hydroclimatiques concomitantes pour permettre d'éventuelles comparaisons d'une région à l'autre.
Avant introduction dans les modèles, la courbe de Von Bertalanffy en longueur sera transformée en courbe en poids de la façon suivante
| wt = W∞ (1-e-K(t-to))n | (5.5) |
où n est l'exposant de la relation longueur-poids. Notons que l'équation peut également être calculée directement si l'on dispose des données poids-âge, comme au paragraphe 5.2.1 (Ricker, 1975) en effectuant la régression de loge (W∞ - wt) sur t, dont la linéarité est très sensible à de faibles variations de W∞ et dont la pente est égale K. Kutkuhn (1966) a utilisé, pour P. duorarum, la méthode d'Allen (1967) en effectuant la régression de
W1/3(t + 1) sur W1/3t.
L'utilisation de ce type de courbe signifie que la croissance est traitée comme une fonction continue. En raison du phénomène de mue, il serait peut-être plus judicieux d'utiliser des fonctions en escalier. Cependant, la mue n'étant pas simultanée chez tous les individus et la croissance se poursuivant partiellement dans l'intermue (Boddeke, Dijkema et Siemelink, 1977), l'approximation par une fonction continue ne devrait pas entraîner de biais considérable. Il faut noter que dans les régions froides où la période d'intermue est longue (plusieurs mois) par comparasion à l'intervalle de temps de base (l'année), on se rapproche beaucoup plus des conditions de mue “simultanée” et cette dernière devient une composante saisonnière importante de l'évolution des biomasses. Un exemple des approches utilisées dans ce cas chez d'autres crustacés pourra être trouvé dans Kurata (1962), Hepper (1967) cité par Conan et Gundesun (1976) et Conan (1975). Ce dernier auteur met en évidence le biais découlant de l'utilisation de la courbe de Von Bertalanffy par comparaison avec un modèle de simulation “en escalier”.
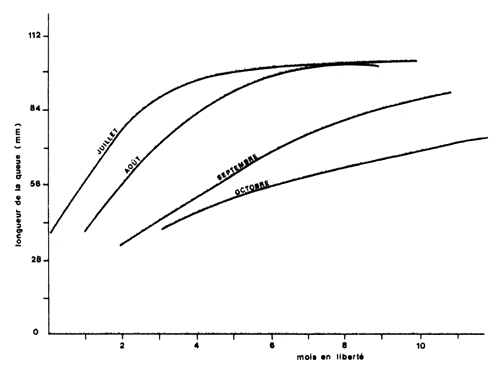
Fig. 38: Courbes de croissance de différentes cohortes pour Penaeus setiferus dans le golfe du Mexique (Klima, 1980)
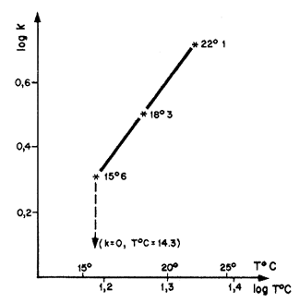
Fig. 39: Variations de K en fonction de la température au Sénégal (d'après Lhomme, 1979)