Les mortalités sont des paramètres extrêmement critiques des études de dynamique des populations car elles sont difficiles à obtenir, en particulier en ce qui concerne la mortalité naturelle, et les conséquences des biais affectant leur estimation sont importantes. Une analyse détaillée des biais possibles sera trouvée dans les ouvrages classiques et, en dehors d'un minimum de rappel de la théorie de base, nous nous attacherons surtout aux méthodes les plus utilisées dans l'étude des stocks de crevettes.
Il y a deux façons d'exprimer numériquement la mortalité dans une population: les taux de mortalité annuels ou espérance annuelle de mort et les coefficients instantanés (Ricker, 1975, p. 8). Dans la suite de cette exposé on utilisera essentiellement ces derniers dont l'usage est le plus largement répandu.
Si le nombre de morts pendant un court intervalle de temps est constamment proportionnel à l'effectif de la population présente, la fraction de cette population présente au début de l'année encore en vie au temps t sera
| Nt/No = e-Zt = e-(F + M)t | (7.1) |
où M, F et Z sont les coefficients instantanés de mortalité naturelle, par pêche, et totale.
Il existe plusieurs façons d'estimer ces paramètres fondamentaux pour la dynamique des populations exploitées que l'on passera en revue dans les paragraphes suivants
Les différentes approches possibles pour l'estimation des mortalités sont:
l'analyse des structures démographiques des captures,
les marquages,
l'analyse des relations cpue/effort,
l'analyse du vecteur de capture, populations virtuelles, analyse des cohortes,
les méthodes approchées.
7.1.1 Les effectifs successifs d'une même cohorte
Le taux de survie des crevettes d'une cohorte peut être estimé approximativement par le rapport des effectifs de cette cohorte à deux âges successifs:
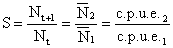 | (7.2) |
La formule reste valable si l'on considère les effectifs moyens pendant deux intervalles de temps successifs. Les effectifs moyens peuvent être remplacés par des indices d'abondance proportionnels aux effectifs moyens à une constante q près comme les cpue en nombres. Comme l'on admet que les nombres décroissent de façon exponentielle en fonction du temps, on en tire
Z = -loge S où Z est le coefficient instanané de mortalité totale.
Si l'effort de pêche peut être considéré comme constant tout au long de la période étudiée, considérée, ou sans tendance nette, une estimation combinée pondérée sur plusieurs intervalles de temps peut être obtenue par des méthodes arithmétiques telles que la méthode de Jackson (Ricker, 1975),
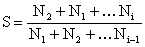 | 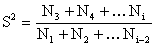 | (7.3) |
ou les méthodes de conception similaires telle que celle de Chapman et Robson (1960) donnant une meilleure estimation de S:
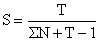 | (7.4) |
où T = N1 + 2N2 + 3N3 +
et ∑N = N0 + N1 + N2 +
Si l'on juge préférable d'obtenir une moyenne non pondérée, elle peut être calculée par moyenne arithmétique simple des valeurs obtenues par l'équation (7.2) ou par régression en fonction du temps des logarithmes népériens des effectifs successifs de la cohorte considérée. La pente de la droite est égale à - Z.
Ces possibilités ont été rappelées dans le souci de présenter un expose succinct mais complet. Cependant, il convient de souligner que, dans le cas des animaux à vie courte comme les crevettes dont l'âge maximum est peu différent de deux ans et qui participent aux captures de façon significative pendant tout juste un an, l'intervalle de temps utile est le plus souvent inférieur à l'année. les variations saisonnières de capturabilité rendent alors difficilement interprétables, en termes de mortalité, les variations apparentes des effectifs.
Cette difficulté, ajoutée à celle de la décomposition des structures de taille en structures d'âge, explique que les méthodes que nous avons rappelées ici aient été très peu utilisées.
Notons cependant que Berry (1967) a utilisé les cpue successives sur de courtes périodes pour calculer des mortalités totales. Cet exemple sera repris au paragraphe 7.1.4. Le marquage est un cas particulier de cette méthode qui sera examiné plus loin.
7.1.2 Les effectifs simultanés de cohortes successives
Un des principaux concepts utilisés dans les calculs en dynamique des populations est que, dans les conditions d'équilibre (recrutement et mortalité constants pendant une période au moins égale à la durée de vie dans la pêcherie) les effectifs observés à un instant donné pour toutes les cohortes d'une population sont assimilables aux effectifs successifs d'une même cohorte. Toutes les équations rappelées au paragraphe précédent restent donc valables si elles sont appliquées aux nombres correspondant à chaque âge dans un échantillon représentatif prélevé à un moment donné sur un stock en équilibre.
La lecture directe de l'âge étant impossible chez les crevettes et la décomposition des distributions de fréquence de taille souvent problématique, la formule de Heincke (in Ricker, 1975) est intéressante car elle ne demande que de connaître l'effectif du premier âge pleinement recruté:
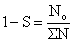 | (7.5) |
où ∑N représente l'effectif total, y compris No.
Dans le cas particulier des crevettes, la nécessité de travailler avec un intervalle de temps court (le mois par exemple) implique que les hypothèses de base de ce procédé ne sont pas remplies lorsque l'on utilise des histogrammes de capture mensuels.
Par exemple: dans le cas où une crevette vit 12 mois en mer et si l'on suppose que la population (ou la génération annuelle) est constituée de 12 cohortes recrutées à chaque mois de l'année (recrutement “continu”), il est certain que les 12 cohortes présentes dans les captures, pendant un mois quelconque de l'année, n'ont pas eu le même recrutement dès lors que des variations saisonnières de recrutement existent, ce qui est le cas le plus général. Il est possible également qu'elles n'aient pas subi la même mortalité s'il existe des variations saisonnières de capturabilité et/ou de l'effort de pêche. L'analyse des effectifs des divers groupes d'âge dans une courbe de fréquence mensuelle ne permet donc pas de calculer une mortalité.
Cette approche reste cependant valable si on utilise la courbe de fréquence des tailles représentant les captures totales de l'année. Une évaluation de la mortalité peut être obtenue en découpant cette distribution en groupes d'âge à l'aide des données sur la croissance moyenne annuelle, si l'on suppose constants le niveau annuel et les variations saisonnières du recrutement1.
C'est la méthode classique des courbes de capture. Garcia (1979) a utilisé cette méthode sur des données correspondant à 3 niveaux d'efforts différents pour estimer la mortalité naturelle (Fig. 48). Pour limiter les biais dus au “découpage”, procédé plus imprécis que la décomposition (voir paragraphe 5.1.1), seules les structures de taille des femelles (les plus étendues) ont été utilisées et des groupes d'âge assez larges ont été considérés (quatre mois). Berry (1969) a également utilisé les histogrammes annuels de longueur des captures pour évaluer la mortalité totale, mais avec un découpage plus fin car il a calculé l'âge moyen correspondant à chaque classe de longueur de l'histogramme. La méthode a également été utilisée par Roessler et al. (1969), pour calculer le taux de survie des stades larvaires, à partir des abondances des différents stades et du temps passé dans chaque stade.
Il est toujours possible de calculer directement les mortalités à partir des distributions d'effectifs en fonction de la taille sans transformation préalable. Cette procédure qui est à l'origine de la méthode dite “des courbes de capture” remonte d'ailleurs à Baranov (1918). Jones et Van Zalinge (MS) en ont proposé l'utilisation dans le cas des penaeïdes du Koweit, lorsque l'on connaît la distribution de fréquence des tailles des crevettes capturées sur une classe d'âge pendant toute la durée de sa vie ou une distribution de fréquence annuelle (ce qui sera souvent une approximation suffisante étant donné les valeurs élevées de M et F que l'on rencontre généralement). Dans ce cas, la comparaison des effectifs cumulés capturés au-delà de la taille L1 avec ceux capturés au-delà de la taille L2 est une estimation de la survie entre L1 et L2, le temps nécessaire pour passer de L1 à L2 dépendant des paramètres de croissance K et L∞.
Les auteurs montrent en particulier que
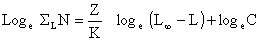 | (7.6) |
où ∑L N est l'effectif cumulé au-delà d'une certaine taille L et C est un terme complexe indépendant de L. La fonction d'ajustement de loge ∑L N sur (Loo-L) est donc une droite de pente égale à Z/K, Z étant supposé constant (Fig. 50). Si la linéarité n'est pas respectée pour tout l'intervalle des tailles étudiées, seule la partie linéaire sera utilisée pour la régression. L'intervalle utilisable doit cependant représenter une proportion suffisante de l'ensemble pour qu'une certaine signification soit accordée à la valeur de Z ainsi calculée.
Il est également clair que la méthode ne peut pas être utilisée sur des distributions contenant un mélange des deux sexes, car les lois de croissance étant en général différentes, il n'existe pas de relation taille-âge unique pour la distribution combinée.
7.1.3 Conclusions
La durée de vie très courte des crevettes, imposant un intervalle de temps inférieur à l'année, les variations saisonnières des phénomènes clés comme le recrutement ou la capturabilité rendent très délicate l'utilisation des méthodes classiques d'estimation de la mortalité. Le plus souvent, les variations seront telles qu'aucune analyse ne pourra être faite à partir des structures d'âge mensuelles.
Les distributions de fréquences annuelles pourront être utilisées mais avec précaution car la décomposition classique en strates d'âge est le plus souvent très difficile. On peut alors procéder à un “découpage” simple qui, basé sur la courbe de croissance moyenne annuelle, peut cependant être une source de biais. Il est d'ailleurs préférable de ne considérer que des groupes d'âge suffisamment larges pour minimiser autant que possible les erreurs dues au découpage, sans oublier que, pour des intervalles importants, l'âge correspondant à la taille moyenne d'un groupe n'est pas identique à l'âge moyen réel du groupe considéré. L'hypothèse d'une mortalité constante avec l'âge doit être considérée avec prudence. En effet, lorsque l'unité de temps est inférieure à l'année, les variations saisonnières peuvent être importantes et difficilement dissociables des variations liées à l'âge (voir paragraphe 7.5.2).
Rappelons enfin que la qualité des résultats obtenus par l'analyse des structures démographiques dépend beaucoup de la représentativité des distributions et de la qualité du système d'échantillonnage.
7.1.4 Cas particulier où F est variable dans le temps
Les méthodes examinées dans les paragraphes précédents supposaient Z constant. Ceci est cependant rarement le cas chez les penaeïdes car l'effort peut varier sensiblement d'une année à l'autre mais également parce que l'utilisation de données correspondant à des intervalles de temps inférieurs à l'année, rendue necéssaire par leur courte durée de vie rend obligatoire la prise en compte des variations saisonnières de l'effort et de F. Pour plus de détails sur ce type de situation on se réfèrera à Ricker (1975, paragraphes 2.6 et 7.4).
7.1.4.1 Méthode de Silliman
Elle peut être utilisée quand on dispose de données sur deux ou plusieurs périodes annuelles d'efforts stables dans une pêcherie. Si les deux périodes sont assez longues par rapport à la durée de vie des crevettes, on peut calculer des valeurs Z1 et Z2 par analyse des structures démographiques, annuelles. On a alors:
| Z1 = F1 + M | |
| Z2 = F2 + M | (7.7) |
| F1/F2 = f1/f2 |
Z1, Z2 et f1/f2 étant connus on peut résoudre ces trois équations pour calculer F1, F2, M et q = F1/f1 = F2/f2
Garcia (1977) a utilisé cette méthode après avoir découpé les histogrammes annuels de captures correspondant à un stock presque vierge au début, légèrement exploité ensuite, puis très exploité (Fig. 48).
7.1.4.2 Méthode de Beverton et Holt (1957)
Lorsque l'on ne dispose pas de périodes de stabilité et que l'effort varie continuellement, ces auteurs proposent (p. 234) une méthode dérivée de la précédente et analogue, par son principe, à celle qui est utilisée au paragraphe sur les marquages. Si l'on dispose d'indices d'abondance moyenne pour plusieurs périodes successives pour lesquelles on connait l'effort moyen, la régression de
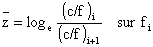
est une droite de pente égale à q et d'ordonnée à l'origine égale à M. Ces deux valeurs provisoires sont ensuite améliorées par itérations successives comprenant le calcul d'un terme correctif.
Paloheimo (1961) propose une modification de la méthode permettant, par régression de Z sur
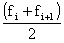
d'obtenir directement q et M sans itérations.
Aucune de ces deux méthodes ne donne des valeurs réellement non biaisées des paramètres, mais la deuxième donne la meilleure estimation possible. Ricker (1973 et 1975) a discuté la justification de la droite de régression prédictive utilisée par ces deux auteurs et propose, étant donné les erreurs vraisemblables sur f et Z, d'utiliser plutôt une régression fonctionnelle (de Nair-Bartlett ou de Wald). Il suggère même, en utilisant une valeur de M obtenue par d'autres méthodes, de calculer une droite fonctionnelle passant obligatoirement par M, conduisant ainsi à une valeur plus précise de q.
Berry (1967) a utilisé ce principe dans un contexte particulier: celui des variations de l'effort à court terme dans une pêcherie de penaeïdes. Considérant qu'en quelques jours la structure du stock ne change pas, il relie les variations de la cpue en nombre à la mortalité. La figure 49 montre les variations de la cpue et celles de la taille moyenne (en nombre de queues/livre). On voit que la cpue diminue quand la taille augmente (mortalité) et augmente quand la taille moyenne diminue (recrutement). Considérant que les tronçons à pente négative reflètent la mortalité totale, Berry calcule des valeurs hebdomadaires de Z qu'il relie tout simplement à l'effort pour obtenir q et X (mortalités naturelles + émigration éventuelle). La dispersion des points sur la figure 51 donne une idée de la variance des estimations de M et q que l'auteur n'a pas calculée mais que l'on aurait pu obtenir en utilisant les équations données par Paloheimo (1961).
7.2.1 Cas général: F et M sont constants
Malgré tous les inconvénients de méthodes de marquage, le problème de la détermination de l'âge chez les crustacés est tel que l'on a inévitablement recours à elles. Ces méthodes ont, de plus, l'avantage de permettre une estimation de la mortalité par pêche et de la mortalité naturelle (estimée par excès). La théorie complète pourra être trouvée dans les manuels de base. Elle a été revue de façon très détaillée par Cormack (1968) et résumée par Jones (1968).
La population marquée peut être traitée comme une population ordinaire, et les principes de l'estimation de la mortalité définis au paragraphe précédent restent valables, le problème de la variabilité du recrutement étant éliminé.
En particulier, si F et M sont constants, le taux de survie peut être donné par le rapport des recaptures dans deux intervalles successifs
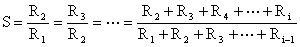 | (7.8) |
et une autre estimation combinée (non pondérée) de Z peut être obtenue en calculant la droite de régression de Ri en i. Cette dernière méthode est la plus utilisée et mérite d'être examinée de façon plus approfondie.
Si l'on considère que Z est constant les effectifs marqués décroissent avec le temps suivant une loi exponentielle et l'évolution de leurs logarithmes est une droite (Beverton et Holt, 1956; Gulland, 1969).
Si les logarithmes népériens des recaptures sont portés en fonction du rang de l'intervalle où elles ont été obtenues, le premier étant numéroté zero1 on obtient une droite de pente (-Zt) et d'ordonnée à l'origine égale à
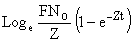
où t indique la durée de l'intervalle de temps. Connaissant Z et N0 le nombre de marques initiales, on peut calculer F et, par soustraction, une valeur, X, de la mortalité résiduelle assimilable à M en première approximation si il n'y a pas d'émigration hors de la zone et pas de mortalité additionnelle. Pour les diverses raisons énumérées au paragraphe 6.8.4, ce sera une estimation biaisée par excès et il peut être préférable de calculer M à partir d'une valeur indépendante de Z obtenue par d'autres méthodes.
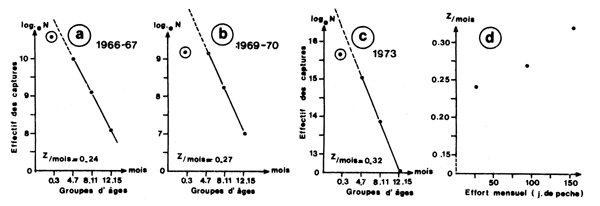
Fig. 48: Courbes de captures correspondant à 3 niveaux d'effort différents chez Penaeus notialis en Côte d'Ivoire (a, b, c) et évolution de la mortalité totale en fonction de l'effort de pêche (d), d'après Garcia, 1977. Les astérisques encerclés représentent des valeurs non utilisées.
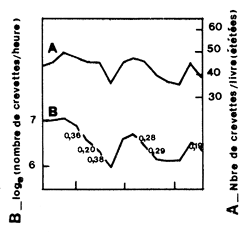 | 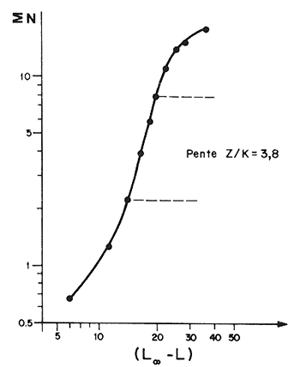 |
Fig. 49: Relation entre les effectifs cumulés et (L∞-L) pour Penaeus semisulcatus au Koweit (d'après Jones et Van Zalinge, M.S.) | Fig. 50: Variations à courte période des cpue en nombre (A) et du calibre moyen (B) chez Penaeus duorarum en Floride (d'après Berry, 1967). Les chiffres indiqués représentent des coefficients de mortalité hebdomadaires |
Si les intervalles de temps sont suffisamment petits, Gulland (1969) montre que si l'on porte le logarithme népérien des recaptures en fonction du point médian de l'intervalle 1, on obtient une droite de pente - Zt et d'ordonnée à l'origine Loge FNot.
Paulik (1963) cité par Jones (1976) préconise, suivant le même principe, une régression pondérée de logeRi/No en fonction du rang de l'intervalle. Le facteur de pondération utilisé est Wi = Ri/No. Cette méthode est utilisable à condition qu'il n'y ait pas de recaptures très faibles ou nulles pour certains intervalles.
Chez les crevettes, la durée d'une expérience de marquage est en général limitée (un à deux mois) à cause de la décroissance rapide des effectifs. Il sera parfois difficile de marquer un nombre suffisant de crevettes en un temps suffisamment court pour pouvoir considérer que le marquage est instantané. Jones (MS) propose de considérer dans ce cas plusieurs groupes différents de crevettes marquées pendant des périodes courtes (deux ou trois jours), de comptabiliser les recaptures séparément par intervalles de temps appropriés, puis de recombiner les recaptures obtenues dans les intervalles de rang identique. On reconstitue ainsi une expérience théorique où le nombre total de marques larguées est la somme des largages individuels et la date du marquage est la date moyenne des divers marquages. Notons que, compte tenu des variations saisonnières prévisibles dans les paramètres, il convient de ne recombiner qu'avec prudence des données de recaptures provenant de marquages trop espacés dans le temps.
Après obtention de Z, la mortalité par pêche peut également être obtenue par l'équation suivante
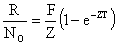 | (7.9) |
qui est l'équivalent du taux d'exploitation de Ricker quand T = 1.R est le nombre total de recaptures obtenues pendant l'expérience de durée T.
Beverton et Holt (1957) indiquent que
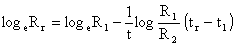 | (7.10) |
où R1, R2 sont les recaptures dans les ler et 2ème intervalles (rang 0 et 1). Une régression de loge Rr en fonction du rang des intervalles a donc pour pente
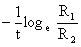 | ce qui est égal à - Z |
et pour ordonnée à l'origine loge R1.
1 t = 0,5, 1,5, 2,5, 3,5, etc.
On peut donc calculer
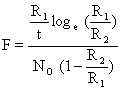 | (7.11) |
et X par (F - Z). Cette méthode a été utilisée par Berry (1967) et Allen et Costello (1968) sur Penaeus duorarum en Floride.
Il est également intéressant de rappeler les méthodes que l'on peut appeler “des libertés cumulées” dont Gulland (1955) est à l'origine. Cet auteur montre que si l'on connaît la durée exacte de liberté (ti) de chaque individu recapturé, si les nombres décroissent suivant une loi exponentielle et lorsque la probabilité de récupérer d'autres marques est nulle, la période moyenne de liberté (∑ti/R = t) est une estimation de 1/Z. On aura donc
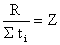 | (7.12) |
Il montre également que
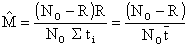 | (7.13) |
et que
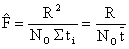 | (7.14) |
Chapman (1961) propose une estimation moins biaisé
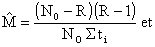 | (7.15) |
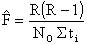 | (7.16) |
dont les variances peuvent être approximativement calculées par
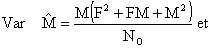 | (7.17) |
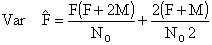 | (7.18) |
Nicholson et Pope (1978) discutent la précision des estimations et leur robustesse quand les hypothèses de base ne sont pas respectées.
7.2.2 Cas où F n'est pas constant dans le temps
Les méthodes de régression supposent que Z est constant. Dans le cas des crevettes ceci est rarement le cas. En effet, l'intervalle de temps utile est le mois ou même la semaine et dans ce cas on assiste à de fortes variations de l'effort de pêche autour de la valeur moyenne. Il est alors possible en première approximation d'utiliser les recaptures par unité d'effort au lieu des recaptures pour la régression. Cette méthode approchée a été utilisée par Kutkuhn (1962), Berry (1967), Garcia (1975), Le Reste et Marcille (1976). Lorsque l'on porte le logarithme des recaptures par unité d'effort en fonction du rang de l'intervalle (0, 1,2 etc.) ou du point médian de l'intervalle (0,5 – 1,5 – 2,5 etc.), on obtient une droite de pente -Zt et d'ordonnée à l'origine égale à
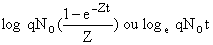
suivant les cas. On peut donc obtenir q par l'ordonnée à l'origine et calculer F par la relation F = qf. Le détail des calculs pourra être trouvé dans Gulland (1969).
De façon plus rigoureuse, Beverton et Holt (1957) proposent la méthode suivante qui suppose que l'effort est constant dans un petit intervalle et qu'il varie brusquement entre deux intervalles (f est une fonction “en escalier” du temps).
Si l'on admet l'équation classique Fr = qfr et si le premier intervalle a le rang 0, ils démontrent que
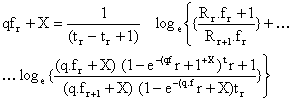 | (7.19) |
et proposent de résoudre cette équation par itérations successives. On peut considérer, dans un premier temps, le terme le plus à droite comme nul et effectuer la régression de
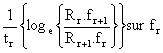
obtenant une droite de pente égale à q et d'ordonnée à l'origine égale à X. Ces valeurs permettent alors d'effectuer la régression complète prenant en compte le terme le plus à droite pour obtenir deux nouvelles valeurs de q et X et répéter le processus jusqu'à stabilisation. La valeur de q ainsi obtenue permet de calculer F connaissant l'effort moyen pendant la période considérée. Cette méthode a été utilisée par Kutkuhn (1966) sur Penaeus duorarum.
Chapman (1961) critique cette méthode de régression car les deux variables ne sont pas indépendantes dans la mesure où l'effort de pêche f est présent dans les deux termes de l'équation. Il donne les équations du maximum de vraisemblance, qui sont trop compliquées à résoudre sans un ordinateur. Il propose donc une méthode approchée par régression multiple qui est commentée par Cormack (1968, p. 495).
Plus récemment, Lucas (1975) travaillant sur des données de Costello et Allen (1968) concernant les crevettes, a proposé une méthode de calcul basée sur le critère du maximum de vraisemblance et un programme d'ordinateur permettant d'obtenir facilement les solutions. Schématiquement, il préconise d'effectuer une régression du logarithme des recaptures par unité d'intensité de pêche sur le rang de l'intervalle (le premier étant O). On obtient donc Z et on peut calculer F et X par l'équation
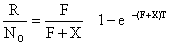 | (7.20) |
où R est le nombre total de recaptures, No le nombre de marques initiales et T la durée totale de l'opération de marquage considérée. Les valeurs F et X ainsi obtenues sont considérées comme de simples valeurs de départ utilisées pour calculer, à l'aide de son programme, les valeurs finales maximisant la fonction de vraisemblance.
L'avantage des méthodes de Chapman (1967) et Lucas (1975) est qu'elles permettent de calculer la variance des paramètres F et X ainsi obtenus.
7.2.3 Cas où F n'est pas constant dans l'espace et où les distributions des populations marquées et naturelles sont différentes
L'un des postulats de base du marquage est que les effets de la pêche sur les populations marquées et non marquées sont identiques. Ceci suppose entre autres que la distribution des crevettes marquées et non marquées est la même ou que l'effort de pêche est distribué au hasard. Ce n'est évidemment pas le cas chez les penaeïdes où la caractéristique essentielle de la distribution est son hétérogénéité et l'existence de gradients. La meilleure solution dans ce cas consiste à quadriller le fond de pêche et à marquer en chaque point un nombre de crevettes proportionnel au rendement du bateau de recherche (Gulland, 1969; Beverton et Holt, 1966). On peut ainsi effectuer des traits courts dans le but de marquer toute la capture. Le traitement des données est ensuite classique.
Cependant, le fond de pêche considéré peut être très vaste et le quadrillage impossible dans les délais impartis. Il peut être également difficile, dans ce cas, d'effectuer le marquage en quelques points seulement et d'attendre un brassage des populations car, étant donné la mortalité élevée des crevettes, la majeure partie des recaptures sera inutilisable. La solution consiste donc à effectuer le marquage dans la ou les zones les plus riches et les plus exploitées, d'utiliser les recaptures par unité d'intensité de pêche (effort par unité de surface) comme au paragraphe précédent (voir également Gulland, 1963) pour obtenir une valeur de q dans la zone considérée. Le calcul de l'intensité globale effective de pêche (“overall fishing intensity”) permet ensuite de calculer F pour l'ensemble du fond de pêche. La dispersion des crevettes se faisant au fur et à mesure du déroulement de l'expérience, la surface qui sera prise en compte augmentera progressivement (Fig. 52). Elle sera délimitée par les zones d'où proviennent les marques si l'on est certain que tout le fond de pêche est prospecté par la flottille.
7.2.4 Cas où les premières recaptures ne sont pas utilisables
Il est possible que, dans le ou les premiers intervalles de temps après le marquage, les recaptures ne soient pas utilisables:
soit parce que la capturabilité des individus marqués est différente de celle des crevettes non marquées par modification du comportement
soit parce que le brassage des populations marquées et non marquées n'est pas terminé. Ce problème a été rencontré par Berry (1967) et Garcia (1975) pour Penaeus duorarum en Floride et P. notialis en Côte d'Ivoire. C'est un cas particulier du problème précédent dans lequel le temps nécessaire au brassage des deux populations est assez court pour que les données correspondantes puissent être rejetées sans une perte trop importante d'information. Il convient alors d'éliminer les données correspondant à cette période et de calculer la régression permettant d'obtenir Z sur les observations ultérieures. L'obtention de F nécessite alors une méthode d'approche par itérations successives pour calculer N'o le nombre de marques au début de la période utile. N'o1 est d'abord estimé grossièrement en retranchant de No le nombre de crevettes (R') recapturées pendant la période litigieuse (T) et en faisant abstraction de la mortalité naturelle.
N'o1 =No - R'
Cette valeur portée dans l'équation (7.11) et les résultats de la régression effectuée avec les données recueillies dans les intervalles utilisables permettent de calculer F1 puis X1 = Z - F1. On peut alors corriger plus exactement No en faisant
N'o2 = (No - R') e -X1T
l'introduction de N'o2 dans (7.11) permet de calculer une seconde valeur de la mortalité par pêche F2 et le processus est répété jusqu'à stabilisation de N'o et X. Cette méthode a été utilisée par Berry (1967) sur Penaeus duorarum.
La démarche serait similaire dans le cas de l'utilisation de l'équation (7.9) pour le calcul de F. La valeur de départ de M peut également être prise dans la littérature si elle existe.
Le même procédé peut être utilisé lorsque la pêche ne commence pas tout de suite après le marquage. On a alors une période préliminaire où la seule mortalité est X, et N'o sera déterminé comme précédemment. Un exemple peut être trouvé dans le travail de Le Reste (1978).
7.2.5 Conclusions
Le marquage est une technique indispensable pour l'étude de la mortalité des crevettes. Les principales difficultés sont les suivantes:
il est pratiquement impossible de marquer les crevettes de petite taille sans biais considérable, sauf peut-être avec le ruban de vinyl,
les nombres marqués sont toujours dérisoires en regard des effectifs considérables de la population,
l'effort de pêche n'est jamais constant et varie fortement, autour de la moyenne dans le meilleur des cas,
les mortalités dues aux marques ne sont pas correctement évaluées et l'application des résultats obtenus par les méthodes expérimentales classiques, en aquarium, n'est pas sans risques.
Les méthodes évoquées dans les paragraphes 3 et 4 ont surtout été mises au point et utilisées pour l'étude des populations naturelles non exploitées et fermées. Le marquage et la recapture sont effectués en général par le scientifique lui-même et son équipe. Pour une étude détaillée des méthodes concernées, le lecteur se réfèrera très utilement à Ricker (1958, 1975), Jones (1976) et à la revue très détaillée de Cormack (1968).
Bien qu'elles aient été très peu utilisées dans le cas des stocks exploités, les quelques essais plus ou moins fructueux qui ont été réalisés sur les crevettes méritent d'être rappelés, à titre d'exemple.
7.3.1 Combinaison des données de marquage, de prise et d'effort - Méthode de Ketchen
La méthode de Leslie permet de calculer la taille de la population, la mortalité par pêche, la mortalité naturelle et la migration. Le principe de base sera trouvé dans Ricker (1975, p. 150). Rappelons que la méthode n'est utilisable que si l'effort appliqué est suffisant pour provoquer une diminution sensible de la cpue. On montre alors que, si mortalité naturelle et immigration sont nulles ou s'annulent, la régression de la cpue sur la prise cumulée est une droite de pente égale à F/f (équivalent de q), d'ordonnée à l'origine qNo et d'abscisse à l'origine = No (où No est la taille initiale de la population (Fig. 53).
Ketchen (1953) a proposé une modification de la méthode, qui a été utilisée chez les penaeïdes par Iversen (1962) et Clark et Caillouet (1973). La population naturelle est soumise à la mortalité naturelle, l'émigration et l'immigration. La population marquée ne peut être modifiée que par les deux premiers phénomènes. Ces deux populations sont traitées comme par la méthode de Leslie (Fig. 54).
Si F est la mortalité par pêche,
y le taux d'émigration,
z le taux d'immigration,
M1 le nombre d'individus marqués initialement et N la population naturelle initiale, le calcul des régressions de la cpue sur la prise cumulée, pour les deux populations, naturelle et marquée, permet d'obtenir Mla et Na les effectifs initiaux apparents. Les pentes des droites sont égales à (F + y)/f et (F + y - z)/f respectivement. On montre aisément que
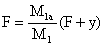
que z peut être calculé par (F + y - z)-(F + y) et que
N = Na (F + y - z)/F
L'un des principaux reproches que l'on peut faire à cette méthode est qu'elle admet implicitement une capturabilité (F/f = q) constante. Si elle varie aléatoirement autour de la moyenne, cela se traduira simplement par une dispersion importante des points. Dans le cas des crevettes cependant, la capturabilité varie beaucoup et de façon non aléatoire. Elle varie en fonction du cycle lunaire (période de 14 jours environ) ainsi que l'a montré Penn (1976). Elle varie aussi saisonnièrement en fonction des conditions ambiantes de température (Penn, 1975) et de turbidité (Garcia, 1977). Dans ces conditions, une expérience menée sur quelques semaines pourrait être biaisée sérieusement par l'existence d'une tendance de q à la hausse ou à la baisse.
C'est pour cette raison que Penn (1976) a considéré la méthode de Leslie comme inapplicable dans son étude.
7.3.2 Evaluations successives des effectifs d'une population fermée - Méthode de Petersen
La méthode de Petersen (recensement simple), appelée aussi méthode de Lincoln, repose sur le principe suivant: lorsque l'on introduit M individus marqués dans une population naturelle d'effectif N et que, par la suite, on en prélève un échantillon significatif, n, contenant m individus marqués, le rapport des individus marqués et non marqués est le même dans l'échantillon et dans la population naturelle

Cette méthode permet donc de calculer la taille d'une population isolée. Utilisée de manière répétée, elle peut donner plusieurs estimations successives permettant de calculer les mortalités. On verra en fin de paragraphe un exemple d'utilisation en ce sens.
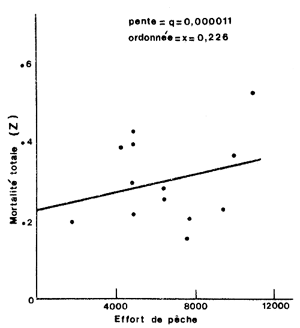 | 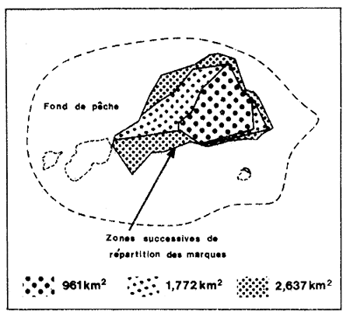 |
Fig. 51: Méthode de calcul de q et x utilisée par Berry (1967) pour Penaeus duorarum en Floride. L'effort est en heures de pêche et l'intervalle de base est la semaine | Fig. 52: Zones successives de répartition des crevettes marquées, en Floride (d'après Costello et Allen, 1968) |
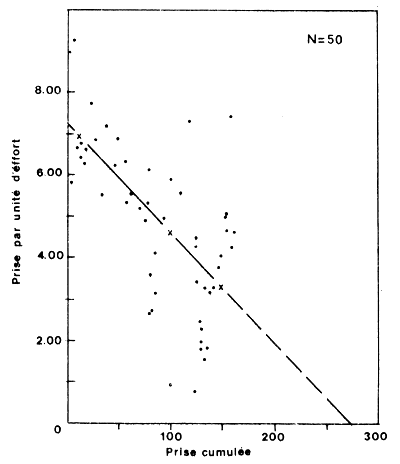
Fig. 53: Application de la méthode de Leslie à un stock de Penaeus duorarum en Floride (d'après Iversen, 1962)
Il a été démontré que cette formule donnait des résultats biaisés et d'autres méthodes de calcul ont été proposées. Celle qui a été utilisée sur les crevettes est préconisée par Bailey (1951),
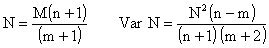
Elle a été appliquée par Penn (1976) sur Penaeus latisulcatus en Australie, Clark et Caillouet (1973) sur Penaeus setiferus et Iversen (1962) sur Penaeus duorarum dans le golfe du Mexique.
L'utilisation de ce type de méthode est délicate car les hypothèses sous-jacentes sont très contraignantes. Il paraît nécessaire de les énumérer (Cormack, 1968):
les animaux ne perdent pas leurs marques,
ils sont toujours correctement identifiés (sans erreur ni oubli),
ou bien la population est réellement isolée ou bien il n'existe ni recrutement ni immigration des animaux non marqués, et la mortalité et la migration des individus est la même qu'ils portent ou non une marque,
l'échantillonnage est aléatoire: tous les animaux marqués ou non ont la même chance d'être recapturés. Si la population est hétérogène, ceci doit rester exact dans chaque strate.
Iversen (1962) a travaillé sur un stock d'adultes de grande taille, en Floride, dans un milieu difficilement contrôlable. Il a, d'autre part, utilisé une marque reconnue par la suite comme relativement meurtrière (disque de Petersen trop large et fixé au centre du premier segment abdominal). La mortalité due au marquage, qu'il a évaluée en aquarium, est très élevée et peut-être trop si on se réfère à ce qui a été dit au paragraphe sur l'évaluation de la mortalité liée à la marque en conditions artificielles (paragraphes 6.8.4 et 7.2.5). Bien qu'il ait obtenu des résultats apparemment cohérents, il faut reconnaître qu'il a travaillé dans les conditions les plus difficiles et que ses résultats (ainsi qu'il le souligne lui-même) doivent être regardés avec prudence d'autant que le nombre d'individus marqués était très faible en regard de la taille de la population.
Caillouet et Jones (1973), se rapprochant un peu mieux des conditions idéales, ont travaillé dans une petite baie peu profonde, isolée de l'estuaire par un filet pour éviter les échanges. Le marquage a été effectué à l'aide d'injections de vaseline fluorescente, éliminant pratiquement la mortalité due au marquage. Malgré ces précautions, les résultats ne sont pas tous cohérents.
Penn (1976) a effectué pour sa part un travail intéressant sur un stock vierge de Penaeus latisulcatus d'une superficie de 1 700 ha dans lequel plus de 13 000 marques (toggle tag) ont été placées. L'opération a eu lieu en période de recrutement faible. L'échantillonnage était assuré par deux crevettiers appointés, travaillant de façon à couvrir toute la zone d'un effort uniforme. Ils ont obtenu, par la méthode de Petersen, plusieurs évaluations successives de la population leur permettant de calculer les mortalités totales et de les séparer en mortalités naturelle et par pêche grâce à la formule du taux d'exploitation de Ricker (1958)
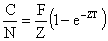
où N est l'effectif de la population au début de l'intervalle d'observation et C la capture pendant toute la période, de durée T.
Là aussi des discordances sont notées entre les résultats à court et à long terme.
En conclusion, ces méthodes peu usitées ont donné, lorsqu'on les a employées, des résultats dont la fiabilité est incertaine parce que les hypothèses de base sont certainement mal respectées.
Pour surmonter les difficultés rencontrées dans l'applications de méthodes discutées au paragraphe précédent, des méthodes plus sophistiquées ont été mises au point reposant sur la possibilité de marquer puis de recapturer à plusieurs reprises les mêmes individus. Utilisées par Barr (1971) sur les crevettes pandalides, la méthode de Schnabel et les autres méthodes similaires n'ont jamais été utilisées chez les penaeïdes que leur fragilité rend impropres aux manipulations et stress repétés au cours des recaptures successives.
La méthode multiple de Robson (1963) est cependant utilisable car elle n'implique pas de recapture multiple et a été préconisée par Jones (MS) pour les penaeïdes du Koweit. Nous nous inspirons beaucoup ici de son exposé.
Le principe de la méthode est le suivant:
Si on effectue un marquage de N1 individus au temp t1 et un autre de N2 individus au temps t2, on peut calculer le taux de survie entre t1 et t2 en comparant les recaptures obtenues à partir de t2 pour les deux marquages. Si les nombres des recaptures (à partir de t2) sont respectivement R12 et R22, et si on admet que les taux d'exploitation sont les mêmes pendant la même période pour les deux groupes de crevettes marquées, on doit admettre que
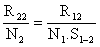
où S1–2 est le taux de survie entre t1 et t2 et N1. S1–2 représente le nombre théorique de crevettes marquées encore vivantes au temps t2 tous les éléments sauf S1–2 étant connus, Z(t2-t1), la mortalité totale entre t1 et t2 sera obtenue par -loge S1–2.
Cette méthode permet d'analyser les variations saisonnières de Z (en liaison avec celles de l'effort de pêche) et également de négliger les recaptures effectuées au début de l'expérience si elles ne sont pas représentatives. En effet, si l'on estime que les recaptures ne sont utilisables qu'à partir de t3 (ou t3> t2> t1) on aura de même
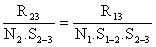
ou encore
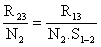
où R13 et R23 sont les recaptures obtenues à partir de t3 pour les deux marquages considérés et N1. S1–2. S2–3 et N2. S2–3 représentent les effectifs marqués encore vivants en t3. On peut donc, comme précédemment, calculer S1–2 et Z(t2 - t1).
Bien qu'encore très peu utilisées chez les penaeïdes, l'éventualité de l'utilisation de ces méthodes doit être examinée car elles ont l'avantage de conduire à une utilisation plus intensive des données concrètes que représentent les statistiques de captures. Elles permettent également de contourner les difficultés parfois rencontrées dans la définition de l'effort.
7.5.1 La méthode d'analyse des populations virtuelles, dont les principes ont été posés par Fry (1949), a été utilisée par Neal (1967) sur Penaeus aztecus du golfe du Mexique. La population virtuelle (V) est définie par Fry comme étant la contribution complète d'une population à la pêcherie. A un moment précis, elle est matérialisée par la prise cumulée réalisée dans les intervalles de temps ultérieurs jusqu'à extinction de la population. On a une évaluation minimale de la population présente (car les individus morts naturellement ne sont pas comptés) et une évaluation maximale du taux d'exploitation que Ricker (1975) appelle taux biostatistique d'exploitation.
Si U(max) est le taux d'exploitation maximum (au sens de Ricker),
Ct la capture réalisée à l'âge t
ft l'effort de pêche exercé sur l'âge t,
on peut définir les éléments suivants:
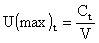
F(max)t = - loge (1 - U(max)t) et
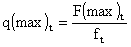
Si l'on connaît par exemple la structure de taille (ou d'âge) des captures par mois (par classes centimétriques ou par catégories commerciales), et le cycle saisonnier de recrutement, on peut reconstituer le vecteur des prises réalisées par mois et par strates de taille (ou d'âge) pour une génération 1 donnée. Les populations virtuelles, totale et par strates de taille (ou d'âge) par mois peuvent ensuite être calculées ainsi que les taux biostatistiques d'exploitation correspondants. Lorsque les taux d'exploitation sont calculés par strates de taille, l'utilisation d'une courbe de croissance moyenne permet de les standardiser par unités de temps comparables (la semaine par exemple dans le tableau ci-après).
Notons que l'existence de variations saisonnières de croissance impliquerait une décomposition préalable des histogrammes de taille mensuels en groupes d'âge avant regroupement au niveau annuel pour le calcul des populations virtuelles.
Cette méthode simple permet également de calculer les pourcentages de la population virtuelle capturée par mois de présence dans la pêcherie, et de faire des comparaisons entre années (Fig. 55). L'utilisation de données économiques (valeur par catégories de taille) permet une approche pratique de la relation entre la répartition saisonnière de l'effort, la taille des crevettes capturées et leur valeur d'une année à l'autre (Neal, 1967). Cet auteur a d'ailleurs limité son analyse à cet aspect pratique et démontre que de faibles variations dans le schéma saisonnier d'exploitation se traduisent par des variations appréciables au niveau des captures.
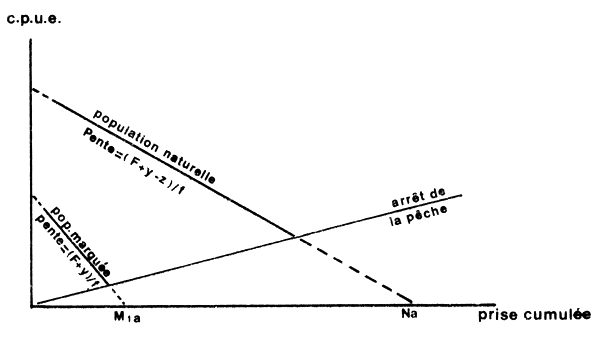
Fig. 54: Principe de la méthode de Ketchen (d'après Ricker, 1975)
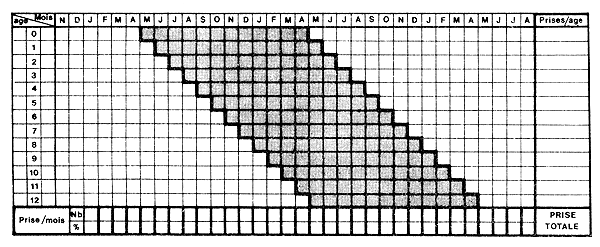
Fig. 55: Représentation schématique de la reconstitution de la population virtuelle pour une génération recrutée en continu pendant 12 mois et dont la durée de vie dans la pêcherie est de 12 mois. Chaque colonne est un histogramme mensuel de capture par âge. Pour chaque génération, les prises en nombre par mois sont obtenues à la dernière ligne du tableau et les prises par âge (mois) dans la dernière colonne (inspiré de Neal, 1967)
| Catégorie (Nb/livre) | Génération | ||||
| 1961 | 1962 | 1963 | 1964 | 1965 | |
| 51–67 | 2 | 3 | 4 | 2 | 6 |
| 41–50 | 10 | 10 | 5 | 6 | 8 |
| 31–40 | 27 | 14 | 19 | 17 | 17 |
| 26–30 | 22 | 12 | 18 | 17 | 18 |
| 21–25 | 5 | 9 | 7 | 9 | 11 |
Taux maximum d'exploitation par semaine (en pour cent) par classe de taille (d'après Neal, 1967)
Cette méthode a été très peu utilisée chez les penaeïdes, l'exemple cité étant le seul connu par les auteurs. Elle a cependant été très utilisée dans d'autres pêcheries et on trouvera dans les travaux de Bishop (1959) et Ricker (1971), 1975) une analyse sur les erreurs liées à la méthode et une discussion des résultats obtenus.
Dans la mesure où les résultats de l'analyse des populations virtuelles ont une portée limitée et sont délicats à interpréter, il peut paraître préférable d'utiliser l'analyse des cohortes.
7.5.2 L'analyse des cohortes
Plusieurs méthodes sont regroupées sous ce vocable. Elle concernent une méthode de calcul séquentiel de la mortalité par pêche et de la taille des populations dont Ricker (1975 p. 194) fait l'historique. Cadima (1977) en rappelle la symbolique et la procédure de calcul à appliquer suivant les éléments disponibles. En général, si M est supposé connu, on peut calculer le vecteur des mortalités par pêche si l'on dispose du vecteur des captures par strates d'âges et une valeur de F, ou de la population, à un âge quelconque. Dans le cas le plus courant, on connaît Ci, Fi et M (supposé constant) dans le dernier intervalle (méthode inverse). Si on désigne par Ni l'effectif présent au début de l'intervalle, Ni l'effectif moyen, Di le nombre total de morts dans l'intervalle, on peut alors calculer
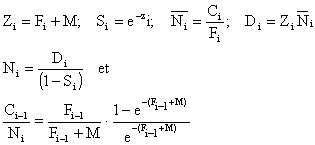
Cette dernière équation résolue par itérations successives ou à l'aide des tables de Schumacher (1970), permet d'obtenir Fi - 1 et le processus peut être répété pour les groupes d'âge plus jeunes jusqu'au début de la séquence de captures, la dernière valeur de Ni ainsi obtenue correspond au recrutement. La méthode peut également être appliquée en partant du premier intervalle (méthode directe ou projection).
La valeur initiale de M supposée connue doit être obtenue par d'autres méthodes (marquage, méthode des efforts variables, méthodes approchées, abaques) ou prise dans la littérature pour la même espèce ou une espèce voisine. Ceci représente, chez les penaeïdes, une grosse difficulté car les valeurs disponibles sont très variables suivant les auteurs.
La valeur initiale de F peut être obtenue par marquage (Garcia, 1977, sur Penaeus notialis) ou toute autre méthode.
Lorsqu'une incertitude subsiste quand à la valeur de M ou de F, l'analyse des cohortes peut tout de même être effectuée en utilisant diverses valeurs pour ces paramètres. Les calculs sont alors rendus plus faciles par l'utilisation des programmes d'ordinateurs actuellement existants tels que Cohort écrit par Fox et disponible à La Jolla. La méthode inverse est alors généralement préférée car toutes les valeurs de F conduisent à une solution possible.
Tous les vecteurs de F ainsi obtenus sont compatibles avec le vecteur de capture disponible et Jones (1961) a montré que, pour un M donné, les estimations de F convergent rapidement vers leur vraie valeur. Cette méthode permet souvent d'éliminer les valeurs les plus improbables de F. Elle est utilisée, par exemple, par Marcille (1978) sur les crevettes de Madagascar.
Pope (1972) a proposé une méthode simplifiée d'analyse des cohortes qui a été modifiée par Jones (1974) pour pouvoir être directement appliquée aux données de capture par strates de taille (captures annuelles par calibres, par exemple).
Si on désigne par les indices 1,2,3 les groupes de taille successifs, l'indice 1 (un) désignant le groupe dont la taille est la plus faible, Jones (1974) montre que
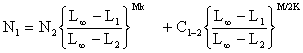
où C1–2 est la capture en nombre des individus dont la taille est comprise entre L1 et L2. On peut écrire pour plus de facilité
| et où | N1 = (N2·X1–2 + C1–2)X1–2 |
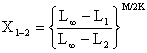 |
Si on connaît Nn-1, l'effectif à la borne inférieure du groupe de taille le plus élevé, on peut donc calculer successivement Nn-2, Nn-3, Nn-4, etc.
Le taux d'exploitation peut être calculé par le rapport des captures au nombre de morts dans l'intervalle (N1 – N2)
(F/Z)1–2 = C1–2/N1 – N2
Le taux de survie et la mortalité totale dans l'intervalle de taille sont donnés par
S1–2·Δt = e-Z1–2·Δt= N2/N1
où Δt est le temps nécessaire pour passer de L1 à L2.
On en tire
Z1–2·Δt = -loge(S1–2·Δt)
F1–2·Δt = (F/Z)1–2·Z1–2Δt
Les valeurs de la mortalité totale sur une base de temps t peuvent ensuite être obtenues par
Z1–2 = M1–2/ 1 - (F/Z)1–2
ou encore Z1–2 = (Z1–2·Δt)/Δt
Le raisonnement est identique si l'on dispose d'une valeur de (F/Z)n-1,n pour le groupe de taille le plus élevé. On en tire par exemple Nn, l'effectif à la borne inférieure du dernier groupe.
Nn = Dn-1,n = Cn-1,n/(F/Z)n-1,n
Les calculs peuvent ensuite être poursuivis comme précédemment. Le tableau suivant résume les calculs effectués sur une cohorte de Penaeus semisulcatus au Koweit par Jones et Van Zalinge (MS).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Calibre Nb/livre | Intervalle de longueur (LC) | 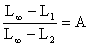 | X = A0,75 | Nombres capturés (106) | Effectifs au début de l'intervalle de taille (106) | F/Z | F (annuel) | Z (annuel) |
| << 15 | 40, 5-1max | - | - | 0,63 | 1,26 | (0,5)1 | - | - |
| 16/20 | 36,2–40,5 | 1,617 | 1,434(1,117)2 | 0,63 | 2,28 | 0,62 | 6,3 | 10,2 |
| 21/25 | 33,2–36,2 | 1,268 | 1,195(1,117)2 | 0,98 | 3,94 | 0,59 | 5,6 | 9,5 |
| 26/30 | 30,9–33,2 | 1,159 | 1,117 | 1,78 | 6,91 | 0,60 | 5,8 | 9,7 |
| 31/35 | 29,1–30,9 | 1,109 | 1,081 | 1,89 | 10,11 | 0,59 | 5,6 | 9,5 |
| 36/40 | 27,6–29,1 | 1,080 | 1,060 | 2,00 | 13,47 | 0,59 | 5,7 | 9,6 |
| 41/50 | 25,3–27,6 | 1,116 | 1,086 | 3,18 | 19,33 | 0,54 | 4,6 | 8,5 |
| 51/70 | 22,1–25,3 | 1,141 | 1,104 | 2,96 | 26,81 | 0,40 | 2,6 | 6,5 |
| 71/110 | 18,5–22,1 | 1,142 | 1,104 | 1,30 | 34,15 | 0,18 | 0,8 | 4,7 |
| 111/140 | 11,2–18,5 | 1,255 | 1,185 | 2,81 | 51,31 | 0,16 | 0,8 | 4,7 |
1 Valeur de départ
2 La valeur entre parenthèses a été utilisée par les auteurs au lieu de la valeur calculée
Il est bon de rappeler que la méthode originale de Pope (1972) donnait, selon l'auteur, des résultats valables jusqu'à des valeurs des mortalités pouvant atteindre au moins 0,3 pour M et 1,2 pour F.
7.5.3 Conclusions
L'utilisation de ce type de méthode se heurte, dans le cas des penaeïdes, à plusieurs difficultés:
(a) Les histogrammes de fréquence des tailles sont difficilement décomposables en groupes d'âge par les méthodes classiques. On est donc le plus souvent contraint à les “découper” en blocs juxtaposés, à l'aide de la courbe de croissance (ou des courbes, s'il existe des variations saisonnières). Pour limiter les biais introduits, il est préférable de choisir des blocs assez larges (le trimestre par exemple), bien que cela comporte un autre risque de biais.
(b) Le recrutement est souvent continu et consiste en un flot permanent, plus ou moins modulé saisonnièrement, d'individus d'âge tr (en réalité cet âge peut varier légèrement au cours de l'année). Dans le cas où l'on considère une seule génération annuelle, la procédure suivie au paragraphe 7.5.1 et sur la figure 55 servira de base à la constitution du vecteur de captures par âge.
Dans le cas le plus plausible cependant, l'existence de variations saisonnières de la capturabilité de l'effort de pêche et de la croissance peut rendre préférable une subdivision en cohortes (base trimestrielle par exemple). La transposition de la méthode classique de constitution des vecteurs de capture, serait d'élaborer les distributions trimestrielles, de les découper en strates d'âge de trois mois (0–2, 3–5, etc.) pour reconstituer, en diagonale, le vecteur de capture (Fig. 57A). Cette procédure suppose en fait, soit que le recrutement se produit au début au trimestre, ce qui n'est pas le cas, soit qu'il est constant dans le temps, ce qui ne peut plus être le cas quand des intervalles inférieurs à l'année sont utilisés car il existe des variations saisonnières du recrutement.
Si les données disponibles le permettent, une meilleure procédure serait de compiler et décomposer des histogrammes mensuels et de constituer ensuite des vecteurs de capture par strates d'âge de trois mois, en suivant la démarche schématisée sur la figure 57B.
(c) Il faut enfin noter que les variations de q observées (si l'on connaît f dans chaque intervalle de temps) seront la résultante de variations en fonction de l'âge et de variations saisonnières, liées de façon pratiquement indissociables.
(d) Compte tenu de la spécificité des stocks à vie courte et du peu d'expérience disponible actuellement en la matière, il convient d'en faire une utilisation prudente après avoir examiné dans quelle mesure les hypothèses de base sont satisfaites. On se réfèrera avec profit dans tous les cas aux travaux de Agger, Boetius et Lassen (1971); Pope (1972, 1978) et Ulltang (1977).
(e) Dans le cas où la ressource est constituée d'une multitude de petits stocks, plus ou moins liés à des baies côtières comme à Madagascar, les migrations d'une baie à l'autre sont susceptibles d'introduire des biais dans l'analyse des captures. Les travaux de Ulltang (1977) et d'Aldenberg (1975) attirent l'attention sur cet aspect de l'analyse des cohortes.
L'industrie se développant en général beaucoup plus vite que la recherche, le facteur temps devient un élément primordial dans l'efficacité de la recherche orientée vers l'aménagement des ressources. L'utilisation de méthodes permettant des évaluations rapides des paramètres de base a été préconisée dès 1956 par Holt et le problème n'a jamais cessé d'être souligné depuis (Holt, 1962; Gulland, 1971; Joseph, 1972; Rikhter et Efanov, 1976; Pauly, 1979). Le problème est particulièrement aigu pour les penaeïdes dont les stocks se trouvent le plus souvent hors des régions où un potentiel de recherche élevé est disponible et pour lesquels les données sont extrêmement rares. Holt (1962) a précomisé l'étude des relations entre les paramètres de base (croissance, mortalité, maturation) par groupes d'espèces pour dégager les lois générales éventuelles, utilisables pour la détermination rapide de ces mêmes paramètres pour des espèces du même groupe, peu ou mal connues. Beverton (1963) a approfondi cette proposition pour les clupeïdes et a noté une certaine cohérence dans les relations entre ces paramètres. Il conclut qu'il existe une relation entre la croissance et la longévité (entre l'âge maximum ou la mortalité naturelle et K) et il indique que la maturation est peut-être encore plus étroitement liée à la mortalité que ne l'est la croissance. Bien que les données sur ce sujet concernant les penaeïdes soient plutôt rares, il nous a paru nécessaire de développer cet aspect et de donner quelques relations pouvant être éventuellement utilisées avec prudence.
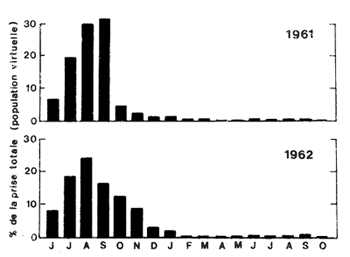
Fig. 56: Comparaison des captures (en % de la population virtuelle) par mois de présence dans la pêcherie pour les générations recrutées en 1961 et 1962 (d'après Neal, 1967)
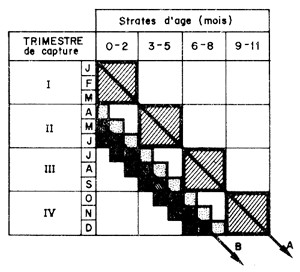
Fig. 57: Représentation schématique de la méthode de constitution de vecteurs de prise
A: procédure classique supposant que le recrutement est localisé au début du trimestre ou qu'il est constant
B: procédure lorsque le recrutement est continu et soumis à des variations saisonnières importantes
7.6.1 Relations entre mortalité naturelle, croissance et longévité
Beverton et Holt (1959), ainsi que Holt (1960, 1962), ont mis en évidence des relations entre l'âge maximum (Tmax), l'âge maximum observé, et la “taille maximale” L∞, ainsi qu'entre M et K pour divers groupes de poissons. L'information sur ce type de relations n'existe pas pour les crevettes où les données sont encore rares et dispersées.
Tanaka (1960), cité par Saville (1977), a donné une relation entre l'âge maximum et M, utilisable pour obtenir une première approximation de M. Ce type de relation doit être utilisé avec prudence et Beverton et Holt (1959) et Beverton (1963) soulignent que leur signification statistique est limitée car la précision des données utilisées est inconnue et les valeurs retenues sont vraisemblablement, dans certains cas, des surestimations ou des sous-estimations: l'âge maximum devrait être la moyenne des valeurs maximales obtenues dans une série d'échantillons de taille identique, ce qui n'est pratiquement jamais le cas. D'autre part, la valeur de Tmax observée dépend de l'intensité de l'échantillonnage.
Ces remarques doivent être présentes à l'esprit, et tout particulièrement en ce qui concerne les crustacés pour lesquels, en l'absence de méthode directe de lecture de l'âge, toute évaluation de l'âge maximum (basée sur l'extrapolation de la courbe de croissance jusqu'à la taille maximale moyenne atteinte ou sur les marquages) est incertaine. Rappelons également les réserves émises par Knight (1968) quand à la signification biologique des paramètres de croissance et l'opinion différente de Kruger (1969).
En dépit des restrictions soulevées, Beverton et Holt (1959) notent que K et M paraissent bien liés. En ce qui concerne les crevettes penaeïdes, les valeurs élevées de K (0,15–0,30/mois, soit 1,8–3,6/an) laissent supposer une mortalité naturelle élevée, ce qui est évident pour des animaux dont la courte durée de vie est connue.
Si l'on porte sur un graphique les valeurs de M et Tmax compilées par ces deux auteurs (Fig. 58), ainsi que la relation de Tanaka (1960) reproduite par Saville (1977), on note:
que cette dernière paraît sous-estimer les valeurs de M,
que pour les penaeïdes dont l'âge maximum est deux ans environ, l'ordre de grandeur de M serait de 2–3/an, soit 0,16–0,25/mois en toute première approximation. Cette estimation, même très grossière, est à comparer avec les valeurs existant dans la littérature et qui vont de 0,04–2,2/mois, soit 1–26/an et devrait permettre de considérer certaines valeurs comme nettement trop élevées.
Beverton (1963) a indiqué que la dispersion des points dans la relation entre M et K rendait impossible l'obtention d'une valeur précise de M à partir d'une valeur de K. Il a cependant indiqué également que cette dispersion était en partie liée à une relation entre ces paramètres et la latitude ou la température de l'eau. Poursuivant cette idée, Pauly (1978) a plus récemment montré une corrélation entre M, L∞, K et T (température moyenne annuelle de surface) sous la forme
log M = 0,1228 - 0,1912 log L∞ + 0,7845 log K + 0,2391 log T
log M = -0,1091 - 0,1017 log W∞ + 0,5912 log K + 0,3598 log T
L∞ étant exprimé en longueur totale en cm, W∞ en grammes et T en degrés Celsius.
Appliqué aux données concernant Penaeus notialis1 de Côte d'Ivoire (K = 2,2; L∞ = 20 cm LT; T = 24°C), ce modèle permet de calculer M = 2,8/an, valeur très proche de celles qui ont été calculées par les méthodes classiques (M≃2,5).
1 D'après Garcia, 1977 - femelles
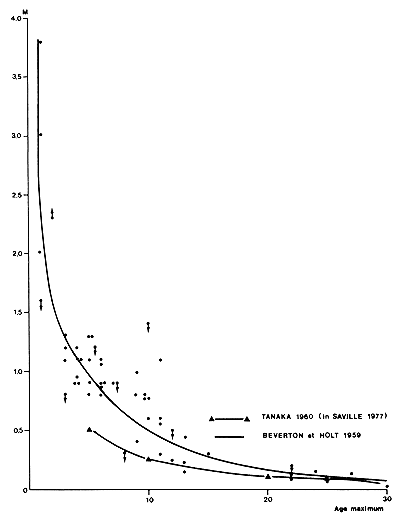
Fig. 58: Relation entre l'âge maximum et la mortalité naturelle (d'après des données de Beverton et Holt (1959) et Tanaka (1960). Cette dernière courbe a été reprise de Saville, 1977)
7.6.2 Relations entre mortalité naturelle et maturité sexuelle
Beverton et Holt (1959) ont cherché, sans grand succès, une relation entre Tmax et le rapport Lm/L∞ où Lm est la taille à la première maturité sexuelle. Holt (1962) rappelle qu'on admet généralement que le rapport Lm/L∞ est d'environ ⅔ (valeur moyenne 0,64 comprise entre les valeurs minimales et maximales de 0,3 et 0,9). En zone tropicale, il a été calculé une valeur moyenne de 0,58 ± 0,03 (au seuil de 95 pour cent) (ISRA/ORSTOM, 1979).
Poursuivant les recherches dans ce domaine encore peu étudié de la dynamique comparative, Rikhter et Efanov (1976) montrent une liaison étroite entre M et tm ou tm50, tm étant l'âge à la première maturité sexuelle et tm50 étant l'âge où 50 pour cent de la population est mûre, appelée encore par Rikhter et Efanov “l'âge de maturation massive”. Ils montrent une relation hyperbolique dont l'équation est
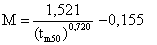
Cette relation empirique doit pouvoir être utilisée pour fixer les ordres de grandeur de M. Il est malheureusement impossible d'en calculer la variance.
A titre d'exemple, Penaeus notialis en Côte d'Ivoire, effectue la première ponte à 7 mois et 50 pour cent des crevettes sont mûres à 10 mois. Le calcul donne M = 1,6 an/ ou 0,13/mois. Cette valeur est donnée à titre tout à fait indicatif car, comme dans la figure 58, la relation utilisée est hyperbolique et donc peu précise dans les petites tailles. Elle est cependant un élément de plus tendant à indiquer que la mortalité naturelle des penaeïdes est élevée certes, mais pas autant que certains travaux pionniers ont pu le laisser croire.
Rikhter et Efanov (1976) suggèrent également que l'âge à la reproduction massive semble pouvoir être assimilé à topt, l'âge optimum défini comme l'âge auquel la biomasse d'une classe d'âge est maximale. Si cette observation est vérifiée, on peut alors utiliser directement pour estimer M, les équations de Beverton et Holt (1966) qui permettent de calculer Lopt lorsque la croissance peut être considérée comme isométrique
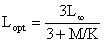
ou celle de Kutty et Qasim (1968) qui permettent de calculer topt quand la croissance est allométrique
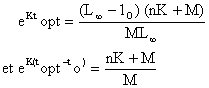
où to est l'âge théorique quand l = o, lo est la taille à l'âge to, et n l'exposant de la relation longueur-poids.
7.6.3 Méthode de la surface balayée
Le principe essentiel du calcul de F par cette méthode est exposé par Beverton et Holt (1956) et elle a été utilisée pour évaluer l'ordre de grandeur de F par Berry (1969) dans la région des Tortugas (Floride) et par Mathews (1973) au Mexique. Cette méthode suppose que F est égal au rapport de l'aire totale balayée par la flottille sur l'aire totale de la zone si les crevettes sont distribuées uniformément et si toutes celles qui se trouvent dans le champ de chalut sont capturées.
Berry a calculé que l'ouverture réelle du chalut est égale à 70 pour cent seulement de la longueur de la corde de dos; il a calculé ensuite l'aire réellement prospectée en éliminant les zones peu visitées, et supposé que toutes les crevettes présentes devant l'ouverture étaient capturées par le chalut. D'après Penn (1976), cette méthode donne des valeurs très surestimées de F pour Penaeus latisulcatus en Australie. Cette observation est confirmée par le travail de Loesch et al. (1976) qui montrent que l'efficacité d'un chalut dans les petits fonds est seulement de 30 à 50 pour cent. Watson (1976) a montré qu'un chalut électrique pêchant des crevettes enfouies dans le sédiment avait une efficacité de 35 à 55 pour cent en pêche de jour. Selon Klima (1976) l'efficacité des chaluts à crevettes serait de 0,55 et 0,68 pour des chaluts de 18 et 21 mètres de cable de dos. D'autre part l'efficacité des chaluts à crevettes dans la capture des poissons serait de 0,25.
Sur un plan général, les remarques suivantes doivent être formulées:
Les crevettes sont très rarement uniformément distribuées. Il existe en général une forte hétérogénéité dans les tailles, les âges et les densités et la pêche n'est pas aléatoire mais extrêmement dirigée grâce au chalut d'essai. Il conviendrait donc, pour en tenir compte, de diviser la zone de pêche en strates et combiner les valeurs élémentaires de F obtenues en les pondérant par la densité dans les strates pour éviter une sous-estimation de F (Beverton et Holt, 1956).
On suppose que toutes les crevettes recontrées sont prises. Ceci est peut être acceptable en Floride, et pour P. duorarum, où la pêche a lieu exclusivement de nuit. Lorsque la pêche a lieu toute la journée, il est clair que l'hypothèse ne tient pas car la capturabilité varie avec l'heure de la journée. Elle varie également saisonnièrement (Garcia, 1973–1977; Penn, 1976) et n'est vraisemblablement jamais totale. Ce biais tend à surestimer la mortalité totale et vient donc contrarier l'effet du biais précédent.
Compte tenu de ces remarques, les valeurs de F obtenues par cette méthode doivent être considérées avec prudence.
7.6.4 Méthode de l'âge ou de la longueur moyenne
Ainsi que le soulignent Beverton et Holt (1956), une économie d'effort peut être réalisée dans certains cas en estimant la mortalité à partir des propriétés “intégrales” des structures démographiques. Par exemple, l'âge moyen des animaux dans les captures peut être relié à Z par l'équation
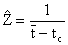 | (Holt, 1965) |
où t est l'âge moyen des individus dont la taille est supérieure à tc l'âge à la première capture.
Lorsque le recrutement est continu, comme cela est le plus souvent le cas chez les crevettes, Ssentongo et Larkin (1973) indiquent que l'estimation non biaisée est
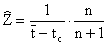
où n est le nombre des échantillons ayant servi à calculer t. La variance est donnée par
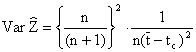
Lorsque l'âge est difficile à déterminer, et c'est le cas chez les crustacés, l'analyse de la taille moyenne des individus dans un stock, et de ses variations au cours de l'exploitation, permet une approche de l'appréciation des mortalités. Beverton et Holt (1956) ont montré que si ℓ est la taille moyenne des individus de taille supérieure à ℓc (taille à la première capture), on peut écrire:
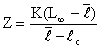
Cette méthode, utilisée par Banerji et George (1967) chez Metapenaeus dobsoni, a permis de calculer une valeur moyenne de Z = 4,04/an ou 0,34/mois.
Ssentongo et Larkin (1973) donnent une méthode dérivée permettant de calculer Z lorsque le recrutement est continu, ce qui est le cas général chez les penaeïdes côtiers

Ces méthodes, malgré leur sensibilité à de faibles variations de lc, sont susceptibles de donner l'ordre de grandeur des mortalités totales.
Le calcul des mortalités chez les penaeïdes est compliqué par la difficulté d'obtenir des structures d'âge fiables ou d'utiliser des marquages sans risque de biais importants. Les méthodes de dynamique comparative (Holt, 1962) sont encore difficilement utilisables car les valeurs disponibles dans la littérature sont trop peu nombreuses et disparates. Les relations générales entre M et l'âge maximum (Tmax) ou M et l'âge à la maturité (tm) sont imprécises pour les longévités les plus faibles et permettent seulement d'obtenir une idée grossière de l'ordre de grandeur de M.
Les premiers marquages réalisés aux Etats-Unis ont fourni des estimations de M si élevées qu'elles rendaient pratiquement inutile toute règlementation. Les résultats obtenus par la suite dans diverses régions du monde conduisent à penser que les première valeurs étaient sans doute surestimées, les techniques de marquage et l'analyse des résultats n'étant vraisemblablement pas encore totalement maîtrisées.
Même si l'on tend de plus en plus à admettre que la protection des jeunes est de nature à améliorer la production, il n'en reste pas moins qu'il est difficile de cerner la valeur exacte des mortalités et en particulier de la mortalité naturelle dont l'importance dans les modèles est primordiale.
A titre d'exemple, on a regroupé, dans le tableau ci-après, quelques valeurs disponibles dans la littérature,
On voit que les valeurs trouvées pour M varient de 0,04 à 2,2 par mois ou 0,48 à 26,4/an. La valeur la plus faible obtenue par Berry est sans doute sous-estimée car la valeur de F qui est obtenue par la méthode de l'aire balayée est vraisemblablement trop élevée (voir paragraphe 7.6.3). La grande majorité des valeurs se trouve entre 0,10 et 0,45 par mois. Ayant été, pour la plupart, obtenues par marquage, elles peuvent être entachées d'erreurs par excès. Cela conduit à des valeurs annuelles de M = 1,2 à 5,4. L'utilisation prudente des méthodes suggérées aux paragraphes 7.6.1 et 7.6.2 devrait permettre d'éliminer les valeurs les moins probables.
Notons enfin que l'on admet souvent que la mortalité naturelle des mâles doit être supérieure à celle des femelles parce que leur croissance est plus rapidement terminée (Holt, 1960, 1962; Beverton et Holt, 1959; Beverton, 1963). En ce qui concerne P. notialis toutefois, Garcia (1975) a montré que le sex-ratio en fonction de l'âge est stable et proche de 50 pour cent, ce qui implique que les mortalités sont identiques pour les deux sexes (Fig. 34). Cette stabilité avait également été mise en évidence par Iversen, Jones et Idyll (1960).
| Espèce | Auteur | M/mois | F/mois | Z/mois | |
| P. duorarum | Kutkuhn | (1966) | 2,2 | 3,8 | 3,0 -6,0 |
| Berry | (1967) | 0,08-0,24 | 0,64-0,92 | 0,88-1,08 | |
| Costello & Allen | (1968) | 0,32-0,44 | 0,12-0,28 | 0,44-0,72 | |
| Berry | (1969) | 0,04-0,08 | 0,36 | 0,40-0,48 | |
| Garcia | (1977) | 0,17-0,32 | 0,15-0,16 | 0,32-0,48 | |
| Garcia | (1979) | 0,21 | - | 0,24-0,32* | |
| P. setiferus | Klima & Benigno | (1965) | 0,32 | 0,24-0,76 | 0,96-1,08 |
| Klima | (1974) | 0,16-0,48 | 0,40-0,48 | 0,65-0,90 | |
| P. aztecus | Klima | (1964) | 0,84 | 0,24 | 1,08 |
| P. indicus | Le Reste | (1978) | 0,21 | 0,27 | 0,48 |
| Marcille | (1978) | 0,15-0,25 | |||
| P. latisulcatus | Penn | (1976) | 0,05-0,13 | 0,04 | 0,09-0,16** |
| Marcille | (1978) | 0,10-0,30 | |||
| Metapenaeus dobsoni | Banerji & George | (1967) | - | - | 0,34 |
| Penaeus plebejus | Lucas | (1974) | 0,2 (adultes) | 0,88 (adul.) | 0,28 |
| 0,88 (juv.) | 0,16 (juv.) | 1,04 | |||
| Metapenaeus monoceros | Marcille | (1978) | 0,10-0,20 | ||
* Pour divers niveaux d'effort
** Stock pratiquement inexploité