En total 50 familles ont été interrogées (25 à Busanza, 25 à Mushonyi). Cet échantillon est, du point de vue statistique, très limité. Les résultats obtenus, ne concernent en effet que ces 50 familles. Une vraie extrapolation pour la Commune, ou même pour les deux secteurs concernés ne peut être faite. Néanmoins, les résultats de l'enquête peuvent être valables dans ce sens qu'ils démontrent des tendances de telle sorte.
Pour avoir une idée de la valeur des données, elles ont été soumises aux différents tests de statistique.
Les données sur lesquelles ont été faites les tests, ont été supposées d'être distribuées normalement. Si cela n'était pas le cas, elles ont été normalisées. La distribution normale peut être utilisée comme approximation d'une distribution binomiale quand le nombre de l'échantillon est plus ou égal à 50.
La distribution normale (distribution Gaussiane) est très utile, grâce à son applicabilité générale; elle sert comme base pour beaucoup de déductions statistiques (VAN MATRE, 1983).
Il existe 4 niveaux différents de mesure:
Très bref, les 4 niveaux différents sont expliqués dans le Tableau 5.1.
Tableau 5.1: Les 4 niveaux de mesure
| caractéristiques | |||
| niveau | ordre | intervalle constante | zéro absolu |
| nominale | - | - | - |
| ordinal | + | - | - |
| intervalle | + | + | - |
| ratio | + | + | + |
La première colonne demande s'il y a un ordre quelconque dans les mesures d'une variable. La deuxième colonne demande s'il y a un intervalle constante entre les classes de mesures. La troisième colonne demande s'il y a la possibilité des valeurs négatives.
Selon les réponses aux 3 questions du Tableau 5.1, le niveau de mesure peut être déterminé.
La méthode appliquée était la suivante (seulement la méthodologie suivie est expliquée, pas la théorie de base):
Faire un tableau avec n colonnes et i rangées (n = le nombre des variables indépendantes, i = le nombre de variables dépendants).
Remplir chaque classe du Tableau avec les fréquences observées. Calculer les fréquences attendues, selon la formule suivante:
 | (1) |
Le Chi-carré est calculé avec la formule (2):
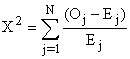 | (2) |
| avec | Oj | = | le nombre observé dans la classe j | |
| Ej | = | le nombre attendu dans la classe j | ||
| N | = | le nombre total des classes | ||
| Calculer le degré de liberté (ddl): | ||||
| ddl | = | (c - 1)×(r - 1) | (3) | |
| avec | c = nombre de colonnes | |||
| r = nombre de rangées | ||||
Comparer le X2calculé avec le X2critique (la valeur X2critique est trouvé dans les Tableaux de X2) pour le ddl approprié.
| Si: | X2calculé > X2critique |
la probabilité d'obtenir par chance un résultat aussi extrême, ou plus extrême que celui qu'on a obtenu, est tellement petite qu'on rejette cette possibilité, c.-à-d. il y a une association, pas dûe au hasard (le résultat est “statistiquement significatif”, cela signifie qu'il n'y a que 5% de chances pour que cette différence soit dûe à une variation aléatoire associée à l'échantillonnage. En d'autres termes, on peut être sûr à 95% que la différence révélée entre les groupes est bien réelle).
| Si: | X2calculé < X2critique |
l'hypothèse zéro (Ho) est acceptée (Ho: il n'y a pas de différence entre les groupes considérés).
Pour tester une hypothèse au niveau ordinal, la méthode appliquée
était la suivante. Par sous-groupe, les données ont été classées dans un
ordre croissant. La médiane (
) a été déterminée (n= pair: : l'observation au [(n+1)/2]ième place; n = impair : : la moyenne entre
l'observation n/2 et n/2 + 1
 | (4) |
| Q3 = (n - Q1) + 1 en ième observation | (5) |
Les limites de confiance (CL) ont été déterminées à 95% et la formule suivante a été appliquée:
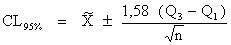 | (6) |
Si on trouvait pour les deux groupes un chevauchement des limites de confiance, l'hypothèse zéro a été acceptée. S'il n'y avait pas de chevauchement des CL l'hypothèse zéro a été rejettée. De ce résultat on pouvait conclure qu'il y avait une différence significative entre 2 groupes qui n'était pas dûe au hasard (dans 95% des cas).
Au niveau interval le t-test a toujours été utilisé pour tester les hypothèses.
Pour chaque groupe déterminé la moyenne et la déviation standard
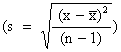 | ont été déterminé. | (7) |
Pour vérifier s'il y a une différence entre les variances, on a fait le F-test.
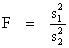 | (8) |
| a) Si F < 2 on peut considérer σ21 = σ22 = σ20 ce qui nous donne: | |
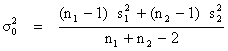 | (9) |
| b) Si F > 2 on considère σ21 = σ22 ce qui nous donne : | |
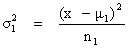 | (10) |
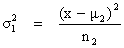 | (11) |
| L'erreur standard est calculée ainsi : | |
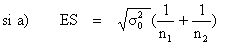 | (12) |
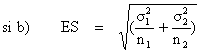 | (13) |
| Le résultat du ES est mis dans la formule (14) : | |
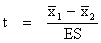 | (14) |
Le résultat obtenu pour t est comparé avec la valeur correspondante dans le tableau t (ddl = n1 + n2 - 2).
Si le tcalculé > t critique on rejette Ho, ce qui montre qu'il y a une différence significative entre les groupes considérés.
Si le tcalculé < t critique on accepte Ho, ce qui montre qu'il n'y a pas une différence significative.
Pour les données au niveau ratio le t-test a été utilisé (cfr 5.5)
Pour chaque groupe de données (niveau intervalle) la moyenne (arithmétique) a été calculée (= paramètre de position).
Un paramètre de dispersion a été calculé, notamment l'écart-type s:
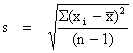 | (15) |
| avec | x = la moyenne de l'échantillon |
| xi = la valeur observée (i = 1,…n) | |
| n = le nombre total de l'échantillon |
Pour examiner la relation entre deux variables, une régression linéaire simple a été faite. La formule théorique du droit de régression est: y = ax + b (16)
| avec | a = le coéfficient de direction |
| b = l'intercept de la droite y |
Ensuite le coéfficient de corrélation a été calculé. La signification du coéfficient de corrélation a été déterminée, compte tenu de la taille d'échantillon. Pour cela, l'abaque de FISHER a été utilisé (MEMENTO, 1984)
Toutes les calculations ont été faites avec l'aide d'un ordinateur IBM avec le tableur SYMPHONY.
