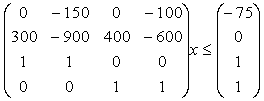 , 0
, 0Back to contents - Previous file - Next file
The
LP matrix generator
The objective function
The LP constraint set
So far, each agro-ecological cell has been assessed in terms of all feasible agricultural land use options of interest in the analysis. At a given level of input, the suitability assessment records expected production of relevant and agro-ecologically feasible cropping activities, in terms of main produce as well as various by-products (e.g., crop residues and by-products), extents by suitability class, input requirements and degradation hazard, i.e., potential soil and productivity loss due to water erosion. This procedure does not derive optimal land use patterns but rather constructs an inventory of potential agricultural land use options with relevant quantitative information. Such an inventory is essential to devising optimal land use patterns that take into account physical, socioeconomic, technological and political objectives and constraints.
It is important to understand that optimal land use cannot be defined per se but always relates to clearly and well specified objectives and constraints. The algorithms applied try to achieve a maximum fulfillment of the level of the specified objective, operating within the given set of constraints. The AEZ productivity assessment forms the back-bone of the physical layer of the constraint set.
In the Kenya study, the objective function and the constraints have been defined by means of linear relationships to allow for application of standard linear programming (LP) techniques. These algorithms are well established and reliable and, most important, can be applied to large scale problems as can arise in this context, with several thousand decision variables and often more than a thousand constraints. The model specification and solution techniques described here have been developed at the International Institute for Applied Systems Analysis (IIASA). More demanding techniques, like non-linear programming or multi-criteria optimization, could readily be applied, but at the expense of a significant increase in computational complexity. For instance, several mathematical techniques exist to handle multiple objectives, through weighting or hierarchical ranking of objectives; also, thorough treatment of uncertainty and production risks could be achieved by means of stochastic optimization techniques.
Before presenting further details of the planning model, it may be illustrative to discuss a simple example of optimal land resource allocation in terms of an LP formulation.
Example 3.1: Allocating Two Crops in Two Land Units, Maximize Food Production
A farmer has a farm that consists of two land units. Land unit LU1, with an extent of 100 ha, is of good quality. Land unit LU2 is of only moderate quality; its extent is 200 ha. Two cropping activities are possible: crop A and crop B. Crop A yields 3 tons per ha on land unit LU1, and 2 tons per ha when cultivated on LU2. It has a good nutritional value: a food energy content of 3000 Kcal per kg, and 5 percent protein content. Crop B gives a yield of 1.5 t/ha and 0.5 t/ha, respectively on land units LU1 and LU2. It contains less energy but more protein: 2000 Kcal food energy per kg of product, a protein content of 20 percent. The farmer wants to:
(1) produce as much food as possible (in energy terms).
(2) produce at least 75 tons of crop B.
(3) obtain a diet with sufficient protein, i.e., the ratio of calories to protein produced must not exceed 40; e.g., in a diet of 2000 Kcal/day there would be at least 50 g protein.
(4) no crop should occupy more than 75 percent of any land unit.
Item (1) states the objective of the farmer; items (2)-(4) formulate constraints to the allocation of land. The simple problem stated above can be written in the format of a standard linear program:
max cx
subject to: Ax <= b
Let x=(x1, x2, x3, x4) be the solution of the land allocation problem; x1 denotes the share of land unit LU1 allocated to crop A, x2 the share of LU1 allocated to crop B. Obviously, the sum of x1 and x2 cannot exceed 1, i.e., land can only be used once. Similarly, x3 and x4 are the shares of land unit LU2 allocated to crop A and B. respectively. For the same reasons, x3 +x4 <= 1 must hold.
The coefficients in the objective function c=(c1, c2, c3, c4) express the food energy content per unit of activity level. For instance, allocating all land in LU1 to crop A would earn c1 = 3 t/ha x 100 ha x 3000 Mcal/t = 900*103 Mcal; allocating all land in LU1 to crop B yields weight c2 = 1.5 t/ha x 100 ha x 2000 Mcal/t = 300*103 Mcal. In the same way, we proceed to determine the remaining weights in the objective function: c3 = 2 t/ha x 200 ha x 3000 Mcal/t = 1200*103 Mcal, and c4 = 0.5 t/ha x 200 ha x 2000 Mcal/t = 200*103 Mcal. Thus vector c becomes c=(900, 300, 1200, 200).
Production q=(q1, q2, q3, q4) obtained per unit of activity is easily calculated. For instance, crop A produces q1 = 3 t/ha x 100 ha = 300 tons on land unit LU1, and q3 = 2 t/ha x 200 ha = 400 tons on land unit LU2; crop B produces q2 = 1.5 t/ha x 100 ha = 150 tons on land unit LU1, and q4 = 0.5 t/ha x 200 ha = 100 tons on land unit LU2. Production of crop B. related to activity levels x2 and x4, defines the coefficients to be used in the first constraint (item (2) above). Note that a 'greater or equal' constraint can be converted to 'less or equal', by multiplying with a factor of -1.
Food energy and protein from each activity are calculated in multiplying production by the respective conversion coefficient. The coefficients to be applied in the constraint concerning the ratio of calories to protein produced (second row of LP constraints matrix) can be obtained from:
a21 = q1 x (3-0.05x40) =
300
a22 = q2 x (2-0.20x40) = -900
a23 = q3 x (3-0.05x40) = 400
a24 = q4 x (2-0.20 x40) = -600
Finally, the condition expressed in item (4) is best translated into simple upper bounds on activity levels, i.e., the maximum share of a land unit to be allocated to any crop is 0.75. In this way we construct all coefficients of the LP:
maxz=(900 300 1200 200)x
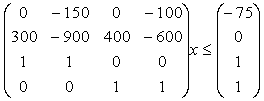 , 0
, 0![]()
s.t.:
Even in this simple example, it would be cumbersome to find an optimal solution without the help of computers and appropriate LP Solver software. For communication with such LP packages, the coefficients of the objective function, constraints matrix, right-hand side, and optionally bounds on variables, must be formatted following an established standard, the MPS file format (see Appendix C). In the MPS file, activities are identified by user defined 8-character column names, constraints are addressed by 8-character row names. In the example given here, ROW00000 refers to the objective function, ROW00001 to ROW00004 identify the four constraints of the LP. Coefficients of the constraints matrix are specified by indicating the respective column (name of activity) and row. Only coefficients with non-zero values need to be specified. Similarly, the non-zero values of the constraint vector b are specified in the RHS section of the MPS file. A default value for lower and upper bounds on activity levels is specified in the specification section (SPECS) of the above file.
The LP Solver can produce detailed information on activity levels, active constraints, etc. The solution x of Example 3.1 is obtained as x=(0.625, 0.375, 0.750, 0.250). Constraint rows 2 to 4 are binding, i.e., the ratio of calories to protein produced is exactly 40, and all the land is used for crop production. Production of crop B is 81.25 tons, exceeding the minimum of 75 tons stated in constraint row 1. The optimal value of the objective function is z=1625*103 Mcal.
Below is a sample MPS input file describing the LP of Example 3.1:
BEGIN
MAXIMIZE
LOWER BOUND 0.0E+00
UPPER BOUND 7.5E-01
SOLUTION YES
PUNCH FILE 19
END
NAME Example 3.1
| ROWS | |||
| N | ROW00000 | ||
| L | ROW00001 | ||
| L | ROW00002 | ||
| L | ROW00003 | ||
| L | ROW00004 | ||
| COLUMNS | |||
| X0000001 | ROW00000 | 900.00 | |
| X0000001 | ROW00002 | 300.00 | |
| X0000001 | ROW00003 | 1.00 | |
| X0000002 | ROW00000 | 300.00 | |
| X0000002 | ROW00001 | -150.00 | |
| X0000002 | ROW00002 | -900.00 | |
| X0000002 | ROW00003 | 1.00 | |
| X0000003 | ROW00000 | 1200.00 | |
| X0000003 | ROW00002 | 400.00 | |
| X0000003 | ROW00004 | 1.00 | |
| X0000004 | ROW00000 | 200.00 | |
| X0000004 | ROW00001 | -100.00 | |
| X0000004 | ROW00002 | -600.00 | |
| X0000004 | ROW00004 | 1.00 | |
| RHS | |||
| RHS1 | ROW00001 | -75.00 | |
| RHS1 | ROW00003 | 1.0000 | |
| RHS1 | ROW00004 | 1.0000 | |
| ENDATA |
Communication with the LP Solver package is via a LP specification file (LP SPECS) and an LP punch file (LP_PNCH). For example, the LP solution file from Example 3.1 is listed below:
| NAME | EXAMPLE 5.1 | PUNCH/INSERT IER= 0 | ITN= 3 | NINF= 0 |
| x1 X0000001 | ROW00002 | 6.25000E-01 | ||
| x1X0000002 | ROW00003 | 3.75000E-01 | ||
| u1 X0000003 | 7.50000E-01 | |||
| x1 X0000004 | ROW00004 | 2.50000E-01 | ||
| ENDATA |
The LP solution file indicates the exit status from the LP Solver package; e.g., IER=0 means that an optimal solution was found. The number of iterations, ITN = 3, and the number of infeasibilities, NINF=O, are also listed. Another simple example, which illustrates how the choice of the objective function affects the resulting land allocation, follows.
Example 3.2: Allocating Two Crops in Two Land Units, Maximize Revenue
The problem specification introduced in Example 3.1 remains the same, but the objective of farmer is changed to:
(1') maximize the net revenue from production.
(2) produce at least 75 tons of crop B.
(3) obtain a diet with sufficient protein, i.e., the ratio of
calories to protein produced must not exceed 40; e.g., in a diet
of 2000 Kcal per day there would be at least 50 g protein.
(4) no crop should occupy more than 75 percent of any land unit.
Item (1') requires different weights in the objective function. Let the prices paid to the farmer be $80 per ton and $200 per ton, respectively for crop A and crop B. Production costs per ha vary depending on crop and land unit, e.g., cultivation of crop A requires $20 per ha on land unit LU1 and $80 per ha on land unit LU2; production costs for crop B are $50/ha and $25/ha, respectively. From this the corresponding weights of the activities in the objective function are derived as:
c1 = 80 x q1 - 20 x 100 =
22000
c2 = 200 x q2 - 50 x 100 = 25000
c3=80 x q3 - 80 x 200=16000
c4 = 200 x q4 - 25 x200 = 15000
Then the coefficients of the LP are constructed:
maxz=(22000 25000 16000 15000)x
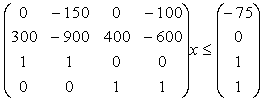 , 0
, 0![]()
s.t.:
The solution x of Example 3.2 is obtained as x=(0.250, 0.750, 0.750, 0.250). Within the limits on mono-cropping, each land unit would be allocated to the economically best use, i.e., land unit LU1 to crop B and land unit LU2 to crop A. The optimal value of the objective function is z=40000 $. Note that the optimal solution obtained in Example 3.1 results in a lower net revenue of $ 38875.
In the Kenya study, the land resource inventory is organized by district, and for some districts the inventory consists of several thousand land units, with many possible crop combinations and livestock related activities to be considered. A spatial resource allocation model has been developed for integrating livestock, crop and fuelwood production sectors within the framework of this study on AEZ Land Productivity Assessment and its application to Potential Population Supporting Capacity and Development Planning in Kenya. Like with any model of this kind, the formulation gets revised and improved as new insights, needs or quantified information becomes available. The strength of the approach lies in its extensive and consistent use of spatial information for assessing agricultural land use options within the context of district development planning. An LP matrix generator program is used to evaluate the cropping options and to generate the LP description in MPS file format.
The LP generator, which is the second item of the sub-menu of option (SF6) DISTRICT ANALYSIS, reads the output from the land productivity assessment and prepares a data file for input to a LP package according to the specifications given in the scenario control input file. Output is generated in standard MPS file format.
In the scenario control input file the user specifies the mode of operation, several program control switches and, optionally, a set of constraints of the linear program which is prepared to subsequently arrive at an optimal land use pattern.
The main program loop starts with reading the cell information record from the land productivity file created by the productivity assessment program, option (SF5). Basic accounting of cell extents takes place, population density relevant to the current cell is retrieved, and the crop combination records relating to the current cell are screened. Each crop combination record is assessed for potential food and feed supplies, crop residues and by-products. Input requirements for production in terms of seeds, fertilizer, power and pesticides are derived by interpolation from a technology matrix and the respective weight in the objective function of the LP is determined. Relevant coefficients of the LP constraint matrix are generated.
After all crop combination records available for the current land inventory cell are processed, the program proceeds with reading the next cell information record continuing this sequence of operations until all cells have been read and dealt with.
Finally, the program turns to the livestock systems feeding and distribution constraints. While processing all the crop combination information, the program also calculates and aggregates data on feed supply by livestock zone. This information is used to generate livestock zone and livestock system specific feed balances and livestock system share constraints. The program ends with writing out the LP specification - objective function, constraint matrix, right hand sides and activity bounds - in standard SPECS and MPS data file format. Since the MPS file format is rather verbose, the resulting output file can become fairly large (several Mb in some cases).
In the following a summary of the linear programming formulation is presented, describing the objective function and constraints that were used in the analysis. For a mathematical description of the model the reader is referred to Appendix B of this report.
The objective function of a district LP describes, in terms of a linear relationship, the economic or political objective of an assessment. It relates the decision variables to a measure of effectiveness and allows for a quantitative evaluation of a specific setting of decision variables and of a potentially large number of feasible options. There are three groups of decision variables:
a) the land use shares, i.e., the share Xkj
of agro-ecological cell j allocated to a particular cropping
activity k,
b) the number of units Lsz of livestock system s kept
in zone z and
c) the feed ration filtsz of feed item I from crop i,
allocated to livestock system s, in period t, in zone z.
These variables form the columns of the LP matrix, the set of activities in the linear program. In the current implementation of the LP model, five different specifications of objective functions are optionally available. They relate to the following objectives:
a) Maximize food production in terms of food
energy (calories) available for human consumption, i.e., food
energy content of production less seed, feed, waste and
conversion losses. For instance, this objective function is used
to assess population supporting capacity.
b) Maximize net revenues of producers, i.e., gross value of
production less the cost of production inputs.
c) Minimize use of arable land required to achieve a given set of
production targets.
d) Minimize cost of production for achieving a given set of
production targets.
e) Maximize domestic self-sufficiency in agricultural products
(in terms of broad commodity groups, such as cereals, root crops,
meats, etc.). The objective is, for a given set of demands, to
maximize the minimum of the jointly achievable individual
commodity group self-sufficiency ratios.
All five types of objective functions outlined lend themselves to linear formulations. They allow for a wide range of assessments relevant to development planning.