Tableau 6.8. Poids sec et dbh de 15 acacias.

Avec les données qui précèdent, deux modèles de régression y = a + b D + c D² et

ln y = a + b D ont été ajustés à l’aide de l’analyse de régression multiple décrite dans Montgomery et Peck (1982),. Pour ces deux modèles, on a calculé la valeur ajustée de R² et l’indice de Furnival. Les résultats sont reportés dans les tableaux 6.9 à 6.12.

Tableau 6.9. Estimation des coefficients de régression et erreur-type pour le modèle de régression y = a + b D + c D².

Tableau 6.10. Table d’analyse de variance pour l’analyse de régression, modèle y = a + b D + c D².

R² = == 0.9463

= 0.9373

Ici, la dérivée de y est 1. Par conséquent,

Indice de Furnival = = = 0.0989.

Tableau 6.11. Estimation des coefficients de régression et erreur-type pour le modèle de régression ln y = a + b D.

Table 6.12. Table d’analyse de variance pour l’analyse de régression – modèle

ln y = a + b D

R² = == 0.9552

= 0.9517

Ici, la dérivée de y est 1/y. L’indice de Furnival, donné par l’équation (6.27), est

Indice de Furnival = == 0.0834

La moyenne géométrique de (1/y) est ici la moyenne géométrique des inverses des quinze valeurs de y du Tableau 6.8.

Dans l’exemple considéré, le modèle ln y = a + b D a un indice de Furnival plus faible, de sorte qu’il est préféré à l’autre modèle y = a + b D + c D². On note également que le second modèle a aussi une valeur ajustée de R² plus élevée.

L’estimation de la croissance et du rendement est un aspect important des sciences forestières. Le terme ‘croissance’ se réfère aux changements irréversibles qui se produisent dans le système sur de brefs cycles de temps, alors que le ‘rendement’ est la croissance globale au cours d’un intervalle de temps donné, et reflète l’état du système à des moments, ou points de temps, donnés. Ces modèles sont importants car de nombreuses décisions de gestion se fondent sur les prévisions de croissance et de rendement. Supposons par exemple que l’on se pose les questions suivantes : Est-il plus rentable de cultiver des acacias ou des tecks, sur une station? La réponse dépend, non seulement du prix, mais aussi des rendements escomptés de ces espèces sur cette station. Ou encore, combien de fois faudrait-il éclaircir une plantation de tecks ? La réponse dépend bien évidemment du taux de croissance attendu de la plantation. Qu’adviendrait-il des tecks s’ils étaient cultivés en mélange avec d’autres espèces? Avec des modèles de croissance appropriés, il est possible de répondre à ce type de questions.

Dans la majorité des modèles, le peuplement est considéré comme une unité d’aménagement. On entend par ‘peuplement’ un groupe d’arbres associés à une station. Les modèles tentent de comprendre le comportement d’un peuplement au moyen d’équations algébriques. Avant d’étudier les différents modèles de peuplement, nous commencerons par décrire quelques-unes des mesures les plus courantes de leurs attributs.

Les mesures les plus courantes des arbres, autres que le simple comptage, sont le diamètre ou la circonférence à hauteur d’homme et la hauteur totale. Pour la définition de ces termes, nous nous sommes référés aux manuels classiques sur ce sujet (Chaturvedi et Khanna, 1982). Quelques attributs des peuplements qui peuvent être dérivés de ces mesures de base, et quelques caractéristiques additionnelles sont décrites ci-dessous.

Diamètre moyen : diamètre correspondant à la surface terrière moyenne d’un groupe d’arbres, ou d’un peuplement, la surface terrière étant la superficie de la section de la tige de l’arbre, mesurée à hauteur d’homme.

Surface terrière d’un peuplement : Somme des surfaces de la section, à hauteur d’homme, des tiges des arbres du peuplement, ordinairement exprimée en m² par rapport à une unité de surface.

Hauteur moyenne: hauteur correspondant au diamètre moyen d’un groupe d’arbres, donnée par la courbe hauteur-diamètre du peuplement.

Hauteur dominante : hauteur correspondant au diamètre moyen des 250 arbres ayant le plus gros diamètre, sur un hectare, donnée par la courbe hauteur-diamètre.

Indice de la qualité de la station : hauteur dominante prévue d’un peuplement, à un certain âge (généralement âge où la croissance en hauteur est à son maximum).

Volume d’un peuplement: volume total de tous les arbres du peuplement, habituellement exprimé en m³ par rapport à une unité de surface.

Suivant le degré de résolution des variables d’entrée, les modèles de peuplement peuvent être classés comme suit: i ) modèles de peuplement globaux ii) modèles de classes de diamètre et iii) modèles d’arbres individuels. Bien qu’il existe des modèles différents pour les peuplements équiennes et non équiennes, la majorité s’appliquent dans les deux cas. En général, les plantations sont principalement constituées d’arbres du même âge et de la même espèce, alors que les forêts naturelles contiennent des arbres d’espèces et d’âges différents. Le terme « équienne » s’applique à des cultures d’arbres qui ont à peu près le même âge, mais on tolère des différences allant jusqu’à 25% de l’âge de rotation si un peuplement n’a pas été exploité depuis au moins 100 ans. En revanche, le terme inéquienne s’applique à des peuplements dans lesquels l’âge des fûts varie considérablement, la fourchette de variation étant ordinairement de plus de 20 ans et, dans le cas de peuplements à rotation longue, de plus de 25% de la rotation.

Les modèles de peuplement globaux prévoient les différents paramètres d’un peuplement directement à partir des variables de régression concernées. Les paramètres habituellement pris en considération sont le volume commercial /ha, le diamètre et la hauteur du peuplement. Les variables de régression sont principalement l’âge, la densité de peuplement et l’indice de qualité de la station. Etant donné que l’âge et l’indice de la qualité de la station déterminent la hauteur dominante, on se contente parfois de prendre en considération cette dernière caractéristique, à la place des deux premières. Les modèles de peuplement globaux peuvent être classés en modèles avec ou sans densité de peuplement comme variable indépendante. Les tables de production normales classiques ne prennent pas en considération la densité de peuplement, étant donné que le terme « normal » sous-entend une densité naturelle maximale. En revanche, les tables de production empiriques supposent une densité naturelle moyenne. Il existe deux sortes de modèles à variable -densité: ceux où le volume présent ou futur est estimé directement par les fonctions de croissance et ceux où le volume du peuplement est obtenu en additionnant des classes de diamètre engendrées mathématiquement. De plus, certains modèles estiment la croissance directement alors que d’autres procèdent en deux étapes (estimation de la densité de peuplement future, estimation du peuplement futur sur la base de cette information, et obtention de la croissance, par soustraction).

Les modèles en classes de diam ètre retracent les variations du volume ou d’autres caractéristiques, pour chaque classe de diamètre en calculant la croissance de l’arbre moyen de chaque classe, et en multipliant le chiffre obtenu par le nombre de fûts répertoriés dans chaque classe. Les volumes de toutes les classes sont regroupés pour obtenir les caractéristiques du peuplement.

Les modèles d’arbres individuels sont les plus complexes et modélisent chaque arbre sur une liste d’arbres-échantillon. Presque tous ces modèles calculent un indice de concurrence des cimes pour chaque arbre, afin de déterminer si l’arbre vivra ou non et, dans l’affirmative, de déterminer sa croissance, en termes de diamètre du fût, de hauteur et de diamètre de la couronne. L’un des critères de distinction entre les types de modèles est le mode de calcul de l’indice de concurrence des cimes. Si le calcul est basé sur la distance (mesurée ou relevée sur une carte) entre un sujet et tous les arbres situés à l’intérieur de sa zone de concurrence, le modèle est dit dépendant de la distance. Si l’indice de concurrence des cimes est calculé uniquement d’après les caractéristiques du sujet et de l’ensemble du peuplement, on a un modèle indépendant de la distance.

Nous allons maintenant décrire quelques modèles appropriés d’une part pour des peuplements équiennes et de l’autre pour des peuplements inéquiennes.

ii) Modèles pour peuplements équiennes

Sullivan et Clutter (1972) ont donné trois équations de base qui forment un ensemble compatible en ce sens que le modèle de rendement s’obtient en sommant les croissances prévues sur des périodes appropriées. Plus précisément, la forme algébrique du modèle de rendement peut être dérivée d’une intégration, au sens mathématique, du modèle de croissance. La forme générale de ces équations est la suivante

Rendement actuel = V₁ = f (S, A₁, B₁) (6.28)

Rendement futur = V₂ = f (S, A₂, B₂) (6.29)

Surface terrière projetée = B₂ = f (A₁, A₂, S, B₁) (6.30)

Où S = Indice de la qualité de la station

V₁ = Volume actuel du peuplement

V₂ = Volume projeté du peuplement

B₁ = Surface terrière actuelle du peuplement

B₂ = Surface terrière projetée du peuplement

A₁ = Age actuel du peuplement

A₂ = Age projeté du peuplement

Dans l’Equation (6.29), on remplace B₂ par l’équation (6.30), et on obtient une équation du rendement futur, en fonction des variables actuelles et de l’âge projeté du peuplement,

V₂=f(A₁,A₂, S, B₁) (6.31)

Prenons un exemple particulier:

(6.32)

On peut estimer directement les paramètres de l’Equation (6.32) grâce à une analyse de régression linéaire multiple (Montgomery et Peck, 1982), avec un nouveau mesurage des données observées sur des parcelles-échantillon permanentes, en gardant V₂ comme variable dépendante et A₁, A₂, S et B₁ comme variables indépendantes.

En posant A₂ = A₁, l’Equation (6.32) devient,

(6.33)

qui permettra de prévoir le volume actuel.

Nous illustrerons une application de l’approche de modélisation à l’aide des équations de Brender et Clutter (1970), ajustées pour 119 peuplements de pins à l’encens de piémont, près de Macon, en Géorgie. L’équation du volume projeté (en acres/ pieds cubes) est

(6.34)

En posant A₂ = A₁, cette équation permet de prévoir le volume actuel, soit

(6.35)

Pour illustrer une application du modèle de Brender-Clutter, prenons le cas d’un peuplement actuellement âgé de 25 ans, d’une surface terrière de 70 pieds²/acre, situé dans une station ayant un indice de qualité de 80 pieds. Le propriétaire veut faire estimer le volume actuel et le volume projeté après dix années de croissance supplémentaires. Le volume actuel est estimé par l’équation (6.35),

= 1.52918 + 0.23 - 0.24634 + 1.71801

= 3.23085

V = 10 ^3.23085 =1,701 pieds³.

Le volume projeté dans 10 ans s’obtient par l’Equation (6.34),

= 1.52918 +0.23 - 0.24634 + 0.65461 -1.22714

= 3.39459

V₂ = 2,480 pieds³

Boungiorno et Michie (1980) présentent un modèle en matrices dans lequel les paramètres représentent i) le passage stochastique des arbres d’une classe de diamètre à l’autre et ii) les recrues de nouveaux arbres, qui dépendent de l’état du peuplement. Le modèle se présente comme suit

(6.36)

. . .

. . .

. . .

où est le nombre prévu d’arbres vivants dans la i-eme classe de taille au temps t.

est le nombre d’arbres de la i-eme classe de taille abattus pendant un intervalle de temps.

g_i, a_i, b_i sont des coefficients à estimer.

Ici le nombre d’arbres dans la plus petite classe de taille est exprimé en fonction du nombre total d’arbres dans toutes les classes de taille et de la récolte pendant un certain intervalle de temps. Sur la même période de référence, les nombres d’arbres dans les plus grandes classes de taille sont des fonctions des nombres d’arbres dans les classes de taille adjacentes. Il est possible d’estimer ces paramètres par une analyse de régression en utilisant des données provenant de parcelles-échantillons permanentes en précisant le nombre d’arbres, et leur état, dans les différentes classes de diamètre, à chaque période, avec un intervalle de temps donné, ainsi que le nombre d’arbres abattus entre deux mesurages successifs.

Nous illustrerons ce qui précède par un exemple très simple, à l’aide des données suivantes, collectées en deux occasions successives, espacées par un intervalle q = 5 ans, dans un petit nombre de parcelles-échantillon permanentes situées dans des forêts naturelles. Les données du Tableau 6.13 indiquent le nombre d’arbres appartenant à trois classes de diamètres, lors des deux mesurages. Supposons qu’aucune récolte n’ait eu lieu pendant cet intervalle de temps, ce qui implique que les quantités h_it; i = 1, 2, …, n sont nulles. Dans la réalité, il se peut que les classes de diamètre soient plus nombreuses, et qu’il faille prendre plusieurs mesures dans un grand nombre de parcelles, en enregistrant le nombres d’arbres enlevés de chaque classe de diamètres entre deux mesurages successifs.

Tableau 6.13. Nombre d’arbres/ha dans trois classes de diamètres, lors de deux mesurages successifs, dans des forêts naturelles.

Les équations à estimer sont les suivantes

(6.37)

En regroupant les données respectives du Tableau 6.13, et en effectuant comme d’habitude l’analyse de régression linéaire multiple (Montgomery et Peck,1982), on obtient les estimations suivantes.

(6.38)

Comme l’ont démontré Boungiorno et Michie (1980), les équations de ce type (6.38)) sont fondamentales pour prévoir l’état futur d’un peuplement et concevoir des politiques d’exploitation optimales sur l’unité d’aménagement. Dans le domaine de l’aménagement des forêts, les modèles de croissance sont généralement utilisés pour comparer différentes options d’aménagement. Avec des modèles de simulation de la croissance, il est possible de comparer les résultats des différentes simulations, notamment les taux de rentabilité interne et d’établir des programmes d’exploitation optimaux. Etant donné que divers modèles permettent d’établir des projections de la croissance et du rendement, il faudra choisir le plus adapté, en tenant compte des données qu’ils nécessitent et de la complexité des calculs qu’ils impliquent. En outre, la validité biologique et la précision des prévisions sont des éléments cruciaux du choix du modèle.

6.3. Ecologie forestière

La biodiversité est la propriété qu’ont les systèmes vivants d’être distincts, c’est à dire différents, dissemblables. Dans cet ouvrage, celle qui nous intéresse est la diversité biologique, ou biodiversité, de groupes ou de classes d’entités biologiques. La biodiversité se manifeste sous deux formes, à savoir la variété et l’abondance relative des espèces (Magurran, 1988). La première est souvent exprimée par l’indice de la richesse en espèces, donné par l’expression,

Indice de la richesse en espèces = (6.39)

où S = Nombre d’espèces dans une collection

N = Nombre d’individus récoltés

Supposons, par exemple, que l’on identifie 400 espèces dans une collection de 10 000 individus, l’indice de la richesse en espèces sera

Indice de la richesse en espèces =

L’augmentation du nombre d’espèces en fonction du nombre d’individus ou de la surface couverte est représentée par une courbe d’accumulation des espèces. La relation entre le nombre d’espèces (S) et la surface couverte (A) est souvent donnée mathématiquement par l’équation S = a Ab , dont on trouvera ci-dessous la représentation graphique pour des valeurs spécifiques de a et b (a = 100 et b = 0.2). Ici , les paramètres a et b devront être estimés empiriquement à l’aide des techniques de régression linéaire avec des données sur la surface couverte et le nombre d’espèces enregistré correspondant.

Figure 6.3. Exemple de courbe espèces- surface

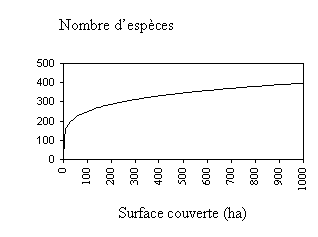
L’équation S = 100A^0.2, va nous permettre de prévoir le nombre d’espèces qu’il serait possible d’obtenir en couvrant une plus grande surface, à l’intérieur de la région d’échantillonnage. Dans l’exemple ci-dessus, nous devrions obtenir ‘458’ espèces pour une surface de 2000 hectares.

Si l’on capture des insectes à l’aide de pièges lumineux, une courbe espèces-individus sera plus utile. Pour trouver une courbe asymptotique, il faut parfois utiliser des équations non-linéaires de la forme,

(6.40)

où S tend vers a lorsque N tend vers ¥ . Autrement dit, a sera le nombre limite d’espèces dans une collection infiniment grande d’individus. Dans ce cas, les paramètres a et b devront être estimés à l’aide de techniques de régression non-linéaire (Draper et Smith, 1966). Un graphique de l’équation (6.40) est donné ci-dessous pour a = 500 et b = 100.