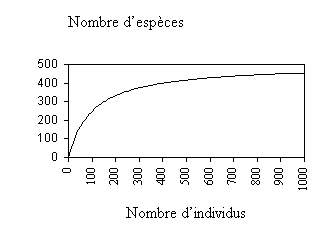
Figure 6.4. Exemple de courbe espèces-individus

L’abondance relative se mesure habituellement par des indices de diversité. L’un des plus connus est l’indice de Shannon-Wiener (H).

(6.41)

où p_i = proportion d’individus dans la i-ème espèce

ln indique le logarithme naturel.

Les valeurs de l’indice de Shannon-Wiener obtenues pour différentes communautés peuvent être vérifiées à l’aide du test t de Student, où t est défini par

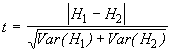(6.42)

et suit une loi de distribution de Student avec n degrés de liberté, où

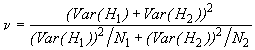
(6.43)

(6.44)

Les méthodes à employer pour calculer l’indice de Shannon-Wiener et tester la différence entre les indices de deux endroits sont illustrées dans ce qui suit.

Le Tableau 6.14 montre le nombre d’individus appartenant à différentes espèces d’insectes attrapés à l’aide de pièges lumineux, dans deux endroits du Kerala ( Matthew et al., 1998).

Tableau 6.14. Nombre d’individus appartenant à différentes espèces d’insectes attrapés à l’aide de pièges lumineux dans deux endroits.

*Etape 1. Lorsque l’on calcule manuellement l’indice de Shannon-Wiener, on commence par dresser un tableau (Tableau 6.15) donnant les valeurs de p_i et p_i ln p_i . Si l’on utilise aussi le test t, il convient d’ajouter au tableau une colonne contenant les valeurs de p_i (ln p_i)².

*Etape 2. La diversité des insectes est H₁ = 2.3716 à Nelliyampathy, alors qu’à Parambikulam elle est de H₂ = 2.4484. Ces valeurs représentent la somme des colonnes p_i ln p_i relatives à chaque endroit. La formule de calcul de l’indice de Shannon-Wiener est précédée d’un signe moins, ce qui annule le signe négatif du à l’utilisation de logarithmes de proportions.

*Etape 3. La variance de diversité des deux endroits peut être estimée à l’aide de l’Equation (6.44).

D’où, Var( H₁ ) -Nelliyampathy = = 0.0029

Var ( H₂ ) -Parambikulam = = 0.0027

Tableau 6.15. Calcul de l’indice de Shannon-Wiener pour les deux endroits

*Etape 4. Le test t permet de comparer les diversités des deux endroits. Les formules appropriées sont données par les Equations (6.42) et (6.43).

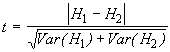
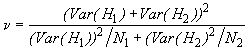
Dans notre exemple, = 1.0263

Les degrés de liberté correspondants sont donnés par

= 695.25

La valeur tabulaire de t correspondant à 695 degrés de liberté (Annexe 2) montre que la différence entre les indices de diversité des deux endroits n’est pas significative.

Par convention, pour des études de la biodiversité on emploie des modèles d’échantillonnage aléatoire. Il convient aussi de se demander quelle taille doivent avoir les échantillons pour estimer un indice de diversité spécifique, quel qu’il soit. Des exercices de simulation fondés sur une structure réaliste des abondances d’espèces ont révélé que l’observation de 1000 individus sélectionnés au hasard était suffisante pour estimer l’indice de Shannon-Wiener. L’estimation de la richesse en espèces requiert parfois jusqu’à 6000 individus (Parangpe etGore, 1997).

Un modèle d’abondance des espèces permet d’obtenir une description complète de l’abondance relative de différentes espèces au sein d’une communauté. La distribution empirique de l’abondance des espèces s’obtient en traçant point par point le graphe du nombre d’espèces et du nombre d’individus. Ensuite, on obtient une distribution théorique approchant la distribution observée. L’un des modèles théoriques utilisés à cet égard, en particulier en présence de populations partiellement perturbées, est la série logarithmique. Celle-ci prend la forme

a x,,, . . . , (6.45)

a x étant le nombre d’espèces constituées d’un individu, a x²/2 le nombre d’espèces de deux individus, etc... Le nombre total d’espèces (S) dans la population s’obtient en sommant tous les termes de la série, ce qui donnera

S = a [- ln (1-x)].

Pour ajuster la série, il faut calculer le nombre d’espèces qui devraient avoir un, deux etc… individus. Ces valeurs prévues sont ensuite rangées dans les mêmes classes d’abondance que celles qui ont été utilisées pour la distribution observée et les deux distributions sont comparées à l’aide d’un test de validité de l’ajustement. Le nombre total d’espèces est bien entendu identique dans les distributions observée et prévue.

Tous les calculs sont illustrés par l’exemple qui suit. Mathew et al. (1998) ont étudié l’impact de la perturbation d’une forêt sur la diversité des espèces d’insectes, dans quatre stations du Western Ghats, dans le Kerala. Dans le cadre de cette étude, ils ont établi une liste de l’abondance de 372 espèces, à Nelliyampathy. Cette liste n’est pas reproduite ici, pour des raisons d’espace, en série log.

*Etape 1. Ranger les abondances observées dans les classes d’abondance. Dans notre cas, on choisit des classes en log₂ (c’est à dire en octaves, ou doubles, des abondances d’espèces). Il suffit d’ajouter 0.5 à la borne supérieure de chaque classe, pour assigner clairement les abondances d’espèces observées à chaque classe. Ainsi, dans le tableau ci-dessous (Tableau 6.16), on constate que 158 espèces ont une abondance d’un ou deux individus, 55 espèces en ont 3 ou 4 etc.

Tableau 6.16. Nombre d’espèces obtenues dans différentes classes d’abondance.

*Etape 2. Les deux paramètres nécessaires pour ajuster la série sont x et a . La valeur de x est estimée par itération du terme suivant

(6.46)

où S = Nombre total d’espèces (372)

N = Nombre total d’individus (2804).

La valeur de x est en général supérieure à 0.9 et toujours <1.0. Il suffit de faire quelques opérations sur une calculatrice, pour obtenir la bonne valeur de x, en essayant différentes valeurs de x dans l’expression jusqu’à arriver à S/N = 0.13267.

La valeur correcte de x est donc 0.96059. Une fois que l’on a obtenu cette valeur de x, on peut facilement calculer a à l’aide de l’équation,

= = 115.0393 (6.47)

*Etape 3. Lorsque l’on a obtenu les valeurs de a et x, on peut calculer le nombre d’espèces qui devraient contenir 1, 2, 3, . . ., n individus. Ceci est illustré ci dessous, pour les quatre premières classes d’abondance correspondant aux sommes cumulées.

Tableau 6.17. Calculs à effectuer pour obtenir le nombre d’espèces prévu dans un modèle en série log.

*Etape 4. L’étape suivante consiste à dresser un tableau du nombre d’espèces prévu et observé d ans chaque classe d’abondance et à comparer les deux distributions à l’aide d’un test de validité de l’ajustement. Le test du ² est l’un des plus utilisés.

Pour chaque classe, calculer ² comme suit.

² = (Fréquence observée – Fréquence prévue)²/ Fréquence prévue (6.48)

Par exemple, dans la classe 1, c ² = (158-163.5809)2 /163.5809 =0.1904. Pour finir, sommer cette colonne pour obtenir la validité globale de l’ajustement, Vérifier la valeur du c ² obtenue dans la table du c ² (Annexe 4) en prenant comme degré de liberté le nombre de classes moins 1. Dans notre cas, , avec 6 degrés de liberté. La valeur de c ² pour P=0.05 est 12.592. On en conclut qu’il n’y a pas de différence significative entre la distribution observée et la distribution prévue. Le modèle en série log est donc bien ajusté aux données.

Lorsque le nombre d’espèces prévues est petit (<1.0), la valeur calculée du c ² peut être très élevée. Dans ce cas, il est préférable de combiner le nombres d’espèces observé dans au moins deux classes adjacentes, et de le comparer avec le nombre combiné d’espèces prévu dans les deux mêmes classes. Les degrés de liberté doivent être réduits en conséquence. Dans l’exemple qui précède, la fréquence prévue de la classe 8 est inférieure à 1, de sorte que l’on a combiné les fréquences observée et prévue de la classe 8 avec celles de la classe 7, pour tester la validité de l’ajustement.

Tableau 6.18. Test de validité de l’ajustement d’un modèle en série log.

La distribution spatiale des végétaux et des animaux est une importante caractéristique des communautés écologiques. C’est habituellement l’une des premières caractéristiques que l’on observe lorsque l’on étudie une communauté et c’est l’une des propriétés les plus fondamentales de tout groupe d’organismes biologiques. Une fois qu’une configuration a été identifiée, l’écologiste peut proposer des hypothèses qui expliquent les causes profondes de cette configuration et les tester. Ainsi, en fin de compte, c’est principalement pour tirer des hypothèses concernant la structure des communautés écologiques que l’on cherche à identifier les distributions spatiales. Nous allons décrire dans cette section l’utilisation de distributions statistiques ainsi que quelques indices de dispersion, pour détecter et mesurer la distribution spatiale des espèces au sein des communautés.

On discerne dans les communautés trois grands types de configuration : aléatoire, en bouquets et uniforme (voir Figure 6.5). Les mécanismes de causalité suivants sont souvent utilisés pour expliquer les répartitions observées dans les communautés écologiques. Dans une population d’organismes, la répartition aléatoire implique un environnement homogène et des comportements non sélectifs. En revanche, les configurations non aléatoires (regroupement en bouquets et uniformes) impliquent que des contraintes soient exercées sur la population. Le regroupement en bouquets laisse penser que les individus sont regroupés dans les endroits les plus favorables; Il peut y avoir diverses causes : le comportement grégaire, l’hétérogénéité de l’environnement, le mode de reproduction etc. Les dispersions uniformes résultent d’interactions négatives entre les individus, telles que la concurrence pour la nourriture et l’espace. On notera que l’identification d’une configuration et l’explication des causes possibles de cette configuration sont deux problèmes différents. De plus, il ne faut pas oublier le caractère multifactoriel de la nature; de nombreux processus (biotiques et abiotiques) interdépendants) peuvent favoriser les configurations.

Figure 6.5. Les trois grands types de distribution spatiale

(a) Aléatoires (b) En bouquets (c) Uniforme

Hutchinson a été l’un des premiers spécialistes de l’environnement à prendre conscience de l’importance des configurations spatiales dans les communautés et à identifier divers facteurs de causalité pouvant conduire à la structuration d’organismes, notamment : i) facteurs vectoriels résultant de l’action de forces environnementales externes (vent, courants de l’eau, et intensité de la lumière) ; ii) facteurs de reproduction, pouvant être attribués au mode de reproduction de l’organisme (clonage et régénération de la descendance) ; iii) facteurs sociaux dûs à des comportements innés (ex : comportement territorial) ; iv) facteurs coactifs, résultant d’interactions intra-spécifiques (ex : concurrence) ; et v) facteurs stochastiques résultant d’une variation aléatoire de l’un des facteurs qui précèdent. Ainsi les processus entrant en jeu dans les configurations spatiales peuvent être considérés comme intrinsèques (ex : facteurs sociaux, coactifs et de reproduction) ou extrinsèques aux espèces (ex : vectoriel). Les causes de la distribution spatiale sont analysées de façon plus approfondie dans Ludwig and Reynolds (1988).

Si des individus d’une espèce sont dispersés sur des unités d’échantillonnage discontinues (ex : cochenilles sur les feuilles des plantes), et si, à un moment donné, on préleve un échantillon du nombre d’individus par unité d’échantillonnage, il est possible de récapituler les données en terme de distribution de fréquence, c’est-à-dire du nombre d’unités d’échantillonnage avec 0, 1, 2, etc… individus. Cette distribution est l’ensemble de données de base qui entre en jeu dans les méthodes de détection des configurations décrites plus loin. On remarquera que les espèces sont supposées apparaître sur des sites ou des unités d’échantillonnage naturelles discontinus, telles que feuilles, fruits, arbres. En général, les relations entre la moyenne et la variance du nombre d’individus par unité d’échantillonnage sont fonction des modes de dispersion de la population. Par exemple, la moyenne et la variance sont à peu de choses près égales dans les répartitions aléatoires, mais la variance est plus grande que la moyenne dans les distributions en bouquets, et plus petite dans les répartitions uniformes. Il existe certains types de distribution de fréquence statistique qui, en raison de leurs rapports variance-moyenne, ont été utilisés comme modèles de ces types de configurations écologiques. Il s’agit de i) la distribution de Poisson pour les configurations aléatoires ; ii) la distribution binomiale négative pour les distributions en bouquets et iii) la distribution binomiale positive pour les distributions uniformes. Ces trois modèles statistiques ont couramment été utilisés dans les études de configuration spatiale, mais il existe d’autres distributions statistiques tout aussi appropriées.

La première étape de la détection du mode de distribution, dans une communauté écologique, implique souvent de tester l’hypothèse " la distribution du nombre d’individus par unité d’échantillonnage est aléatoire ". La distribution de Poisson a déjà été décrite dans la Section 2.4.2. Si l’hypothèse de la distribution aléatoire est rejetée, la distribution peut tendre vers le regroupement en bouquets (cas habituel) ou uniforme (exception). Si la direction tend vers une dispersion en bouquets, la concordance avec la distribution binomiale négative doit être testée et certains indices de dispersion, basés sur le rapport de la variance à la moyenne, peuvent être utilisés pour mesurer le degré de regroupement. Ce cas n’est pas abordé ici, d’une part parce que les configurations uniformes sont relativement rares dans les communautés naturelles, et d’autres part parce que la distribution binomiale a déjà été décrite dans la Section 2.4.1.

Avant de poursuivre, quelques réserves s’imposent. Tout d’abord, le non-rejet d’une hypothèse de distribution aléatoire signifie seulement qu’aucun caractère non aléatoire n’a été détecté à l’aide de l’ensemble de données spécifié. Deuxièmement, les hypothèses proposées doivent être raisonnables, c’est-à-dire soutenables et fondées à la fois sur le bon sens et sur des connaissances biologiques. Ce second point est lié par d’importantes ramifications au premier. Il n’est pas rare qu’une distribution statistique théorique (ex. distribution de Poisson) ressemble à une distribution de fréquence observée (c’est-à-dire qu’il y a concordance statistique entre les deux), même si les hypothèses qui sous-tendent ce modèle théorique ne sont pas vérifiées par l’ensemble de données. Il s’ensuit que l’on peut accepter une hypothèse nulle même si elle n’a pas de justification biologique. Troisièmement, les conclusions ne doivent pas être basées uniquement sur les tests de signification. Toutes les sources d’information disponibles (écologiques et statistiques) devraient être utilisées ensemble. Ainsi, le non rejet d’une hypothèse nulle, basée sur une petite taille d’échantillon, devrait être considéré comme une faible confirmation de ladite hypothèse. Enfin, il faut avoir présent à l’esprit que la détection d’une configuration spatiale et l’explication de ses causes possibles sont deux problèmes différents.

L’utilisation de la loi binomiale négative pour la vérification de configurations en bouquets est décrite ici. Le modèle binomial négatif est vraisemblablement la loi de probabilité la plus couramment utilisée pour les distributions en bouquets (également appelées distributions " contagieuses " ou " agrégatives "). Lorsque deux des conditions requises pour l’emploi du modèle de Poisson ne sont pas vérifiées - à savoir la condition 1 (toutes les unités d’échantillonnage naturelles ont la même probabilité de contenir un individu) et la condition 2 (la présence d’un individu dans une unité d’échantillonnage est sans influence sur le fait qu’elle soit occupée par un autre individu) - on obtient en général un rapport variance- moyenne élevé du nombre d’individus par unité d’échantillonnage. Comme on l’a vu plus haut, ceci laisse penser que l’on est en présence d’une configuration en bouquets.

La loi binomiale négative a deux paramètres, m , le nombre moyen d’individus par unité d’échantillonnage et k, un paramètre lié au degré de regroupement. Les étapes de la vérification de la concordance entre la distribution de fréquence observée et la loi binomiale négative sont décrites ci-dessous.