*Etape 1. Formulation de l’hypothèse; il s’agit de tester l’hypothèse selon laquelle le nombre d’individus par unité d’échantillonnage  suit une loi de distribution binomiale négative, ce qui dénote l’existence d’une dispersion non-aléatoire ou en bouquets. S’il n’arrive pas à rejeter cette hypothèse, l’écologiste peut avoir un bon modèle empirique pour décrire un ensemble de données de fréquence observées, sans que ce modèle explique quels sont les causes profondes possibles de cette configuration. Autrement dit, il faut se garder de déduire la causalité uniquement sur la base de nos méthodes de détection du mode de dispersion.

*Etape 2. Le nombre d’individus par unité d’échantillonnage est résumé sous la forme d’une distribution de fréquence, autrement dit du nombre d’unités d’échantillonnage avec 0, 1, 2, …, r individus.

*Etape 3. Calculer les probabilités P(x) de la loi binomiale négative. La probabilité de trouver x individus dans une unité d’échantillonnage, c’est à dire que dans P(x), x soit égal à 0, 1, 2, …, r individus, est donnée par la formule,

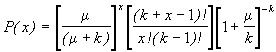(6.49)

Le paramètre m est estimé à partir de la moyenne de l’échantillon (). Le paramètre k mesure le degré de regroupement et tend vers zéro pour le regroupement maximal. On peut obtenir une estimation de k par itérations successives de l’équation suivante :

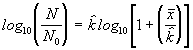(6.50)

où N est le nombre total d’unités d’échantillonnage dans l’échantillon, et N₀ est le nombre d’unités d’échantillonnage avec 0 individus. Dans un premier temps, on remplace dans le second membre de l’équation par une estimation initiale. Si le second membre de l’équation est inférieur au premier, on essaie une valeur plus élevée de , et l’on compare à nouveau les deux membres. On itère ce processus (en choisissant de manière appropriée des valeurs inférieures ou supérieures de ) jusqu’à obtenir une valeur de vers laquelle les deux membres de l’équation convergent. Une bonne estimation initiale de pour la première itération est obtenue grâce à la formule,

= (6.51)

où s² est la variance de l’échantillon estimée.

Lorsque la moyenne est basse (inférieure à 4), l’Equation (6.50) fournit un bon moyen d’estimer . Par contre, si la moyenne est élevée (supérieure à 4), la méthode itérative n’est efficace que si le regroupement de la population est généralisé. Ainsi, lorsque la moyenne () de la population et la valeur de (le paramètre de regroupement calculé à partir de l’équation (6.51)) sont toutes les deux supérieures à 4, l’équation (6.51) est préférée à l’équation (6.50) pour estimer.

Une fois que l’on a obtenue les deux statistiques, et , on calcule, avec la formule (6.49), les probabilités P(x) de trouver x individus dans une unité d’échantillonnage, où x = 0, 1, 2, …, r individus,

=

=

=

=

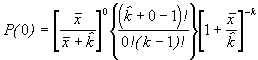
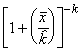
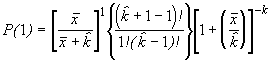
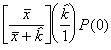
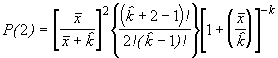
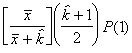
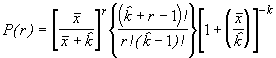
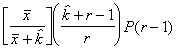
*Etape 4. Trouver les fréquences binomiales négatives théoriques. Le nombre théorique d’unités d’échantillonnage contenant x individus s’obtient en multipliant chaque probabilité binomiale négative par N, le nombre total d’unités d’échantillonnage dans l’échantillon. Le nombre de classes de fréquence, noté q, est aussi déterminé selon la méthode décrite pour le modèle de Poisson.

*Etape 5. Test de la validité de l’ajustement. Le test du ² sera effectué suivant la procédure décrite dans la Section 3.5.

Nous allons maintenant examiner un exemple d’ajustement d’une distribution binomiale négative. On trouve souvent des larves d’abeilles charpentières dans les pédicelles des inflorescences des yuccas (arbre à savon), dans le sud du Nouveau Mexique. Un écologiste spécialiste des insectes qui étudiait les modes de dispersion spatiale de ces abeilles, a récolté au hasard un échantillon de larves sur 180 pédicelles de yucca. Les données observées sont résumées dans le tableau de fréquence suivant,

où x est le nombre de larves d’abeilles par pédicelle et f_x est la fréquence de pédicelles de yucca ayant x = 0, 1, 2, …., r larves. Dans cet exemple, r = 10. Le nombre total d’unités d’échantillonnage est

N =

= 114 + 25 + …..+ 0 + 1 = 180

et le nombre total d’individus est

= (0)(114) + (1)(25) + (9)(0) + (10)(1) = 171

La moyenne arithmétique de l’échantillon est

= 0.95

et sa variance est

s² =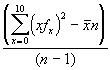

= 2.897

*Etape 1. Hypothèse: L’hypothèse nulle est « les larves d’abeilles charpentières se regroupent en bouquets sur les pédicelles des inflorescences de yucca ». Il convient donc de tester la concordance (du nombre d’individus par unité d’échantillonnage) avec la loi binomiale négative. La variance supérieure à la moyenne laisse penser que les abeilles sont distribuées en bouquets.

*Etape 2. Distribution de fréquence, f_x : La distribution de fréquence observée, sa moyenne et sa variance, sont données plus haut.

*Etape 3. Probabilités binomiales négatives, P(x) : Une estimation de , obtenue à l’aide de l’Equation (6.51) avec = 0.95 est s²= 2.897 est

= 0.4635

Les valeurs de et étant l’une et l’autre inférieures à 1, l’Equation (6.50) peut être utilisée pour donner une estimation de . En prenant les valeurs N =180 et N₀ =114 dans le premier membre de l’équation (6.50), on obtient la valeur 0.1984. Ensuite, en posant = 0.4635 dans le second membre de l’Equation (6.50), on obtient :

Itération 1 :

= 0.2245

Puisque le second membre de l’équation donne une valeur supérieure à 0.1984, on remplace par une valeur plus petite que 0.4635, dans l’Equation (6.50). En choisissant = 0.30 on trouve,

Itération 2 :

= 0.1859

Cette valeur est proche de 0.1984, (mais à présent plus petite). Pour l’itération suivante, on choisit donc une valeur de légèrement plus grande. En prenant =0.34, on a

Itération 3 : = 0.1969

Là encore, pour l’itération suivante, on essaye une valeur de légèrement plus élevée. Pour =0.3457,

Itération 4 : = 0.1984

Cette valeur numérique est identique à la valeur fournie par le premier membre de l’Equation (6.50) de sorte que, dans notre exemple, la meilleure estimation de est 0.3457. Enfin, les probabilités, individuelles et cumulatives, de trouver 0, 1, 2, et 3 larves par pédicelles [pour =0.95 et =0.3457, où ] sont données dans le Tableau 6.18.

Les probabilités cumulées, après avoir trouvé 4 individus dans une unité d’échantillonnage sont de 94.6%. Les probabilités restantes, de P(5) à P(10) sont donc de 5,4%, soit

P(5⁺) = 1.0 - 0.946 = 0.054.

Tableau 6.18. Calcul de P(x), les probabilités binomiales négatives, pour x individus (abeilles) par unité d’échantillon (pédicelle de yucca)

*Etape 4. Fréquences théoriques, E_x : Elles s’obtiennent en multipliant les fréquences théoriques par le nombre total d’unités d’échantillonnage (Tableau 6.19)

Tableau 6.19. Calcul des fréquences théoriques d’unités d’échantillonnage contenant un nombre variable d’abeilles.

*Etape 5. Validité de l’ajustement : Le test statistique c ² est calculé comme suit,

c ² =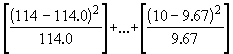

= 0.00 + …+ 0.01= 1.18

On compare cette valeur du critère de test à la table des valeurs critiques du c ² avec (nombre des classes – 3)= 3 degrés de liberté. La valeur critique, au seuil de probabilité de 5%, est de 7.82 (Annexe 4), et, puisque la probabilité d’obtenir une valeur de c ² égale à 1.18 est nettement inférieure à cette valeur, on ne rejette pas l’hypothèse nulle. Le modèle binomial négatif apparaît donc comme un bon ajustement des données observées, mais nous souhaitons obtenir une confirmation supplémentaire (par exemple, un ensemble de données indépendant) avant de conclure que les larves d’abeilles charpentières sont effectivement réparties en bouquets. On notera que si, dans notre exemple, on laisse descendre les valeurs théoriques minimales jusqu’à 1.0 et 3.0, les valeurs de c ² sont respectivement 2.6 et 2.5 – niveaux encore nettement inférieurs à la valeur critique.

Tableau 6.20. Calculs pour le critère de test c ²

Pour détecter des configurations spatiales, on peut préférer aux distributions statistiques certains indices faciles à calculer, comme l’indice de dispersion ou l’indice de Green, si les unités d’échantillonnage sont discrètes.

(i) Indice de dispersion : Le quotient variance-sur-moyenne ou indice de dispersion (ID) est

ID = (6.52)

où est s² sont respectivement la moyenne et la variance de l’échantillon. Le quotient variance-sur-moyenne (ID) est utile pour évaluer la concordance d’un ensemble de données avec la série de Poisson. Par contre, ce n’est pas un bon paramètre pour mesurer le degré de regroupement. Si la population est regroupée en bouquets, le ID est fortement influencé par le nombre d’individus dans l’échantillon, et ne sera un bon indice comparatif de regroupement que dans le cas où n est le même dans chaque échantillon. L’indice de Green (GI), qui est une version modifiée de l’ID, indépendante de n, est donné par la formule,

GI = 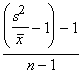(6.53)

GI varie de 0 (pour la dispersion aléatoire) à 1 (pour le regroupement maximal). On peut donc utiliser l’indice de Green pour comparer des échantillons dont le nombre total d’individus, la moyenne et le nombre d’unités d’échantillonnage dans l’échantillon varient. En conséquence, parmi les nombreuses variantes de l’ID qui ont été proposées pour mesurer le degré de regroupement, le GI semble la plus appropriée. Les valeurs du GI pour la population de cochenilles peuvent être obtenues comme suit

Comme la valeur maximale du GI est 1.0 (si les 171 individus étaient apparus dans une seule pédicelle de yucca), cette valeur représente un degré de regroupement relativement faible.

Il est bien connu que les forêts, en tant qu’écosystèmes, varient considérablement au fil du temps. Il est important, aussi bien du point de vue scientifique, que sur le plan de l’aménagement, de comprendre ces processus dynamiques. On s’est beaucoup intéressé dans le passé à l’estimation de la croissance et du rendement des forêts, qui est l’un des éléments de ces processus. Cependant plusieurs aspects tout aussi importants sont liés à la dynamique des forêts, notamment les effets à long terme de la pollution de l’environnement, les variations des cycles écologiques dans les forêts, la dynamique, la stabilité et la résilience des écosystèmes tant naturels qu’artificiels etc… Ces différents objectifs des applications requièrent des approches de modélisation radicalement différentes. Ces modèles sont si complexes qu’il est impossible, ne serait-ce que d’en donner un bref aperçu ici, de sorte que l’on s’est limité à tenter de donner une description simplifiée de quelques-uns de ceux qui pourraient être utilisées dans ce contexte.

Tout processus dynamique est configuré par l’échelle de temps caractéristique de ses composantes. Dans les forêts, ces échelles peuvent se compter en minutes (processus stomatiques) en heures (cycle diurne, dynamique sol-eau), en jours (dynamique des nutriments, phénologie), en mois (cycle saisonnier, accroissement), en années (croissance et sénescence des arbres), en décennies (stades de végétation successifs des forêts) ou en siècles (réaction d’une forêt à un changement climatique). L’échelle de temps que l’on privilégiera dépend de l’objet du modèle. On la détermine habituellement avec des données agrégées décrivant les processus qui ont des échelles de temps différentes, mais le niveau d’agrégation dépend du degré de validité comportementale visé.

Pour rassembler des données sur la dynamique des forêts, au niveau du macro-environnement, la méthode traditionnelle consiste à établir des parcelles échantillons permanentes et à faire des observations périodiques. Dernièrement, la télédétection par satellite et par d’autres dispositifs a élargi le champ d’application de la collecte de données historiques précises sur les forêts. Sans entrer dans les détails de ces autres approches possibles qui sont complexes, nous allons expliquer dans cette section comment sont utilisées les parcelles échantillons permanentes, dans les recherches forestières à long terme, et illustrer un modèle de succession forestière par un exemple très simplifié.

Le meilleur moyen d’étudier la dynamique des forêts naturelles est d’établir des parcelles échantillons permanentes. Bien que la taille et la forme des parcelles et la nature et la périodicité des observations varient suivant l’objet de l’enquête, nous proposons quelques directives valables pour les études écologiques en général ou pour les études sur l’aménagement des forêts.

Il convient de choisir des stations représentatives dans chaque catégorie de forêts et d’établir des parcelles échantillons pour observer en détail la regénération et la croissance. Les parcelles doivent être assez grandes - au moins un hectare (100 m x 100 m) – et être situées dans différentes stations ayant des peuplements de densités variables. L’idéal est d’avoir au moins 30 parcelles dans une catégorie de forêt particulière pour étudier la dynamique et les interactions entre le peuplement et la station. Les parcelles peuvent être délimitées par de petites tranchées aux quatre coins. Il faut aussi dresser une carte du lieu, indiquant l’emplacement exact de la parcelle. Un inventaire complet des arbres se trouvant dans les parcelles doit être fait en marquant chaque arbre avec des bagues d’aluminium numérotées. L’inventaire précisera certains paramètres de base, comme le nom de l’espèce et la circonférence à hauteur d’homme sur les arbres adultes (gbh sur écorce > 30 cm) et sur les gaulis (gbh sur écorce >10 cm <30 cm). Les plantules (gbh sur écorce < 10 cm) peuvent être comptées dans des sous-parcelles d’une taille de 1m x 1m, sélectionnées de manière aléatoire ou systématique.

Des informations sur les propriétés du sol de chaque parcelle sont rassemblées dans plusieurs fosses d’observation, dont les on regroupera les différentes données. Les paramètres de base seront le pH du sol, le carbone organique, la texture du sol (teneur en gravier, sable, limon et argile), température et réserves d’humidité du sol. Des observations concernant certaines caractéristiques topographiques, comme la pente, l’aspect, la proximité d’une source d’eau etc…, sont aussi enregistrées pour chaque parcelle.

Nous allons maintenant concentrer notre attention sur un modèle particulier, appelé "modèle de Markov", qui nécessite l’utilisation d’outils mathématiques appelées matrices. Une description élémentaire de la théorie des matrices est fournie à l’Annexe 7, pour les non initiés. Dans un modèle de Markov du premier ordre, l’évolution future d’un système est déterminée par son état présent, et ne dépend pas de la manière dont cet état s’est développé. L’enchaînement de résultats produits par un modèle de ce type est souvent appelé chaîne de Markov. L’application de ce modèle à des problèmes concrets est limitée par trois contraintes majeures, à savoir: le système doit être classé en un nombre fini d’états, les transitions doivent avoir lieu à des instants discrets, même si, pour le système en cours de modélisation, ces derniers peuvent être si proches qu’ils peuvent être considérés comme continus dans le temps, et enfin les probabilités de transition ne doivent pas varier avec le temps. Il est possible de modifier dans une certaine mesure ces contraintes, quitte à augmenter la complexité mathématique du modèle. On peut utiliser des probabilités variant en fonction du temps, ou des intervalles variables entre les transitions et, dans les modèles de Markov d’ordre plus élevé, les probabilités de transition dépendent, non seulement de l’état actuel, mais aussi d’un ou plusieurs états antérieurs.

Les modèles markoviens ont une valeur potentielle particulièrement élevée, mais jusqu’à présent ils ont été peu utilisés en écologie. Toutefois des études préliminaires laissent penser que, lorsque les systèmes écologiques étudiés affichent des propriétés markoviennes, et plus particulièrement d’une chaîne de Markov stationnaire de premier ordre, il est possible de faire plusieurs analyses intéressantes et importantes du modèle. Par exemple, l’analyse algébrique d’une matrice de transition déterminera l’existence d’une série d’états transitoires, d’ensembles fermés d’états ou d’un état absorbant. Une analyse plus approfondie permet de fractionner la matrice de transition de base et d’étudier séparément les différentes composantes, ce qui simplifie le système écologique à l’étude. L’analyse d’une matrice de transition peut aussi conduire à calculer les temps de passage moyens d’un état à l’autre et la durée moyenne d’un état particulier, depuis son début. En présence d’états fermés ou absorbants, il est possible de calculer la probabilité d’absorption et le temps moyen d’absorption. Un ensemble transitoire d’états est un ensemble dans lequel chaque état peut en fin de compte être atteint à partir de tout autre état faisant partie de l’ensemble, mais qui est abandonné lorsque l’état entre dans un ensemble d’états fermés ou dans un état absorbant. Un ensemble fermé se distingue d’un ensemble transitoire en ce sens que, une fois que le système est entré dans un état quelconque de l’ensemble fermé, l’ensemble ne peut pas être abandonné. Un état absorbant est un état que l’on ne peut plus quitter, c’est à dire où l’auto remplacement est complet. C’est pourquoi le temps de passage moyen représente le temps moyen nécessaire pour passer à travers un état particulier de la succession, et le temps moyen d’absorption est le temps moyen pour atteindre une composition stable.

Pour construire des modèles apparentés à celui de Markov, les principales informations nécessaires sont les suivantes: une classification quelconque qui, jusqu’à un degré acceptable, sépare les états de la succession en des catégorie définissables, des données servant à déterminer les probabilités de transferts ou les vitesses auxquelles les états passent, au cours du temps, d’une catégorie de cette classification à une autre et des données décrivant les conditions initiales à un temps donné, habituellement suivant une perturbation bien établie.

Prenons pour exemple les interactions forêts (terres boisées) – prairies sur de longues périodes de temps dans des paysages naturels. Il est bien connu que lorsque les forêts naturelles sont continuellement perturbées par l’homme ou affectées par des incendies répétés, elles peuvent retourner à l’état de prairie. L’inverse peut aussi se produire, en ce sens que des prairies peuvent se transformer en forêts dans certains environnements propices. Dans cet exemple, les forêts et les prairies sont deux états que le système peut prendre avec des définitions bien adaptées même si, dans la réalité, il peut y avoir plus de deux catégories.

Le Tableau 6.21 présente les données collectées dans 20 parcelles échantillons permanentes, sur l’état de la végétation se trouvant dans les parcelles classées dans la catégorie forêts (F) ou prairies (G), en 4 occasions successives, espacées de 5 ans.

Les probabilités historiques de transition entre les deux états possibles, sur une période de 5 ans, sont indiquées dans le Tableau 6.22. Ces probabilités ont été estimées en comptant le nombre de fois où se produit un type particulier de transition, disons F-G, sur une période de 5 ans, et en divisant ce nombre par le nombre total de transitions possibles dans les 20 parcelles, en vingt ans.

Tableau 6.21. Etat de la végétation dans les parcelles témoin, en 4 occasions

Tableau 6.22. Probabilités de transition, relatives aux changements successifs se produisant dans un paysage (intervalle = 5 ans)

Ainsi, les parcelles qui sont initialement des forêts ont une probabilité de 0,7 de rester à l’état de forêts à la fin de la période de 5 ans, et une probabilité de 0,3 d’être convertie en prairie. Les surfaces qui, au départ, sont des prairies ont une probabilité de 0,8 de rester dans cet état et une probabilité de 0,2 de retourner à l’état de forêt. Aucun des états n’est donc absorbant ou fermé, mais chacun représente une transition de la forêt à la prairie, et vice-versa. En l’absence d’états absorbants, le processus de Markov prend le nom de chaîne ergodique et l’on peut étudier toutes les conséquences de la matrice des probabilités de transition en exploitant les propriétés fondamentales du modèle markovien.

Les valeurs du Tableau 6.22 montrent les probabilités de transition d’un état quelconque à un autre après un intervalle de temps (5ans). Les probabilités de transition après deux intervalles de temps peuvent être dérivées directement en multipliant la matrice de transition en une étape par elle-même, de manière à ce que, dans le cas plus simple où il est existe deux états, les probabilités correspondantes soient données par la matrice suivante:

Sous une forme condensée, on peut écrire :

P⁽²⁾ = PP

De même, la matrice de transition en trois étapes s’écrit :

ou P⁽²⁾ = P⁽²⁾P

En général, pour la n-ème étape, on peut poser :

P⁽ⁿ⁾ = P^(n-1)P (6.54)

Pour la matrice du Tableau 6.22, les probabilités de transition à l’issue de deux intervalles de temps sont:

Et à l’issue de quatre intervalles de temps :

Si une matrice de probabilités de transition est élevée à des puissances successives jusqu’à atteindre un état où toutes les lignes de la matrice sont identiques, formant un vecteur de probabilité fixe, la matrice est appelée matrice de transition régulière. La matrice donne la limite à laquelle les probabilités de passer d’un état à un autre sont indépendantes de l’état initial, et le vecteur fixe de probabilité t exprime les proportions d’équilibre des différents états. Par exemple, le vecteur des probabilités d’équilibre est 

Donc, si les probabilités de transition ont été correctement estimées et restent stationnaires - ce qui implique qu’il ne se produit aucun changement majeur dans les conditions environnementales ou dans le modèl e d’aménagement de la région considérée - le paysage finira par atteindre un état d’équilibre formé d’environ 40% de forêt et environ 60 % de prairie.

Lorsque, comme dans cet exemple, il n’existe pas d’états absorbants, on peut aussi estimer, au moyen de calculs complexes, l’intervalle de temps moyen nécessaire pour qu’une surface de prairie se transforme en forêt, (et vice-versa) compte tenu des conditions qui prévalent dans la région, c’est à dire les temps moyens de premier passage. En d’autres termes, si l’on choisit une surface au hasard, pendant combien de temps devrons nous attendre, en moyenne, pour que cette surface devienne une forêt ou une prairie, c’est-à-dire les temps moyens de premier passage à l’équilibre.

6.4. Biologie de la faune sauvage

L’échantillonnage par lignes interceptées est une méthode couramment employée pour estimer l’abondance de la faune. Cette méthode peut être grossièrement décrite comme suit. Supposons que l’on ait une surface de limites connues et de taille A et que l’on veuille estimer l’abondance d’une population biologique, sur cette surface. La technique d’échantillonnage par lignes interceptées requiert l’établissement d’au moins une ligne de parcours (ou transect) sur la surface considérée. On note le nombre d’objets détectés (s_i) et les distances perpendiculaires (x_i), de la ligne jusqu’aux objets détectés. On peut aussi enregistrer la distance d’observation r_i et l’ angle d’observation q _i, qui permettent de retrouver x_i à l’aide de la formule x = r sin(q ). Soit n la taille de l’échantillon. L’échantillon correspondant de données potentielles est indexé par (s_i, r_{i, q i} , i = 1,..., n). La méthode est représentée graphiquement à la Figure 6.6.

Figure 6.6. Représentation graphique de l’échantillonnage par lignes interceptées

r

x

Quatre hypothèses cruciales doivent être posées pour obtenir des estimations fiables de l’abondance de la population à partir d’une enquête par lignes interceptées, à savoir: i) Les points situés directement sur la ligne ne sont jamais omis ii) Les points sont fixes à leur emplacement d’observation initial, dont ils ne bougent pas avant d’être détectés et ils ne sont jamais comptés deux fois iii) Les distances et les angles sont mesurés avec exactitude iv) Les observations sont des événements indépendants.

Une estimation de la densité est donnée par la formule suivante :

(6.55)

où n = Nombre d’objets observés

f(0) = Estimation de la fonction de densité de probabilité des valeurs des distances, à distance nulle

L = Longueur du transect

Pour estimer la quantité f(0) on part du principe qu’une distribution théorique, comme la distribution semi-normale ou la distribution exponentielle négative, est un bon ajustement de la distribution de fréquences observée des valeurs des distances. Dans le contexte de l’échantillonnage par lignes interceptées, ces distributions prennent le nom de modèles de fonction de détection. L’ajustement de ces distributions peut aussi être testé en calculant les fréquences théoriques et en effectuant un test de validité de l’ajustement du c ². Une autre variante permet d’estimer la distribution de fréquence observée par des fonctions non-paramétriques comme la série de Fourier, et d’estimer f(0). L’idéal est d’effectuer au moins 40 observations indépendantes pour obtenir une estimation précise de la densité. On trouvera dans Buckland et al. (1993) une description détaillée des différents modèles de fonction de détection  qui entrent en jeu dans les échantillonnages par lignes interceptées.

Prenons par exemple l’échantillon suivant de 40 observations sur la distance perpendiculaire (x), en mètres séparant des troupeaux d’éléphants de 10 transects de 2 km de long chacun, disposés au hasard dans un sanctuaire de faune

32,56,85,12,56,58,59,45,75,58,56,89,54,85,75,25,15,45,78,15

32,56,85,12,56,58,59,45,75,58,56,89,54,85,75,25,15,45,78,15

Ici n = 40, L = 20 km. Si la fonction de détection est semi-normale, la densité de troupeaux d’éléphants dans le sanctuaire de faune peut être estimée par la formule,

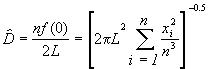
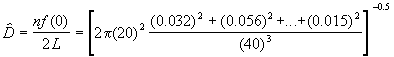
= 13.63 Troupeaux/ km²

Dans le cas d’une fonction de détection semi-normale, l’erreur-type relative, ou au choix, le coefficient de variation (CV) de l’estimation de D est donné par la relation,

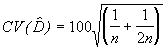(6.56)

=

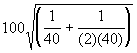
= 19.36%

Le domaine vital, ou aire de répartition naturelle, est l’espace dans laquelle vit normalement un animal, qu’il le défende ou non comme son territoire, et qu’il le partage ou non avec d’autres animaux. En général, le domaine vital ne comprend pas les zones de migration ou de dispersion. Les données géographiques concernant un ou plusieurs animaux servent de base pour calculer le domaine vital, et toutes les statistiques sur ce sujet sont obtenues grâce à la manipulation de ces données pendant une certaine unité de temps. Il existe plusieurs méthodes d’évaluation du domaine vital, mais elles rentrent généralement dans 3 catégories, suivant qu’elles sont basées sur i) un polygone ii) un centre d’activités ou iii) des fonctions non paramétriques (Worton,1987), chacune ayant ses avantages et ses inconvénients. Nous allons illustrer ce qui précède à l’aide d’une méthode basée sur un centre d’activité.

Si x et y sont deux co-ordonnées indépendantes de chaque position et n est la taille de l’échantillon, le point () est considéré comme le centre d’activité

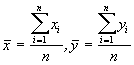(6.57)

Le calcul d’un centre d’activité simplifie les données géographiques en les réduisant à un point unique. Cette mesure peut être utile pour séparer les domaines des individus dont les points relatifs aux données géographiques empiètent largement les uns sur les autres.

L’une des principales méthodes proposées pour mesurer le domaine vital est basée sur un modèle elliptique à deux variables. Pour estimer le domaine vital par cette approche, on commence par calculer certaines mesures de dispersion élémentaires concernant le centre d’activité, comme la variance et la covariance,

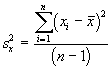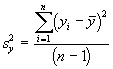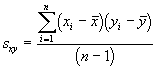, , (6.58)

ainsi que l’écart-type, et . Ces statistiques de base peuvent être utilisées pour déterminer d’autres variables, comme les valeurs propres, connues aussi sous le nom de racines caractéristiques ou latentes, de la matrice 2 x 2 des variances-covariances. Les équations des valeurs propres sont les suivantes:

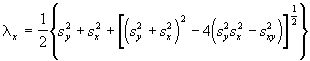(6.59)

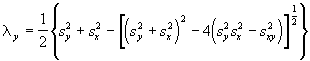(6.60)

Ces valeurs mesurent la variabilité intrinsèque de la dispersion des positions selon deux axes orthogonaux (perpendiculaires et indépendants) passant par le centre d’activité.

Bien que l’orientation de ces nouveaux axes ne puisse pas se déduire directement des valeurs propres, leurs pentes peuvent être déterminées par les relations,

b₁ (pente de l’axe principal [le plus long]) = 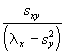(6.61)

b₂ (pente de l’axe secondaire [le plus court]) = (6.62)

Les ordonnées y à l’origine ainsi que les pentes des axes complètent les calculs nécessaires pour tracer les axes de variabilité. Les équations

(6.63)

décrivent respectivement l’axe de variabilité principal et l’axe de variabilité secondaire.

Considérons un ensemble de données géographiques représenté par un nuage de points orienté parallèlement à l’un des axes de la grille. Les écart-types des coordonnées x et y (s_x et s_y) sont proportionnels aux longueurs des axes principal et secondaire (ou semi-principal et semi-secondaire) d’une ellipse passant par ces points. En utilisant la formule de l’aire d’une ellipse, A_e= p s_xs_y, on peut obtenir une estimation de la taille du domaine vital. Dans le reste de notre démonstration, nous prendrons pour ellipse type l’ellipse ayant des axes de longueur 2s_x et 2s. Si l’axe principal et l’axe secondaire de l’ellipse sont égaux, la figure est un cercle et la formule devient A_c= p r², où r = s_x = s_y.

L’un des inconvénients évidents de cette mesure est que les axes calculés de données géographiques naturelles sont rarement parfaitement alignés avec les axes d’une grille déterminés arbitrairement. Il s’ensuit que les valeurs s_x et s_y dont dépend l’aire de l’ellipse, peuvent être affectées par l’orientation et la forme de l’ellipse. Ce problème n’existe pas dans les modèles circulaires de domaine vital. Il existe deux méthodes qui permettent de calculer des valeurs de s_x et s_y, corrigées pour l’orientation (covariance). Dans la première, chaque ensemble de coordonnées est transformé comme suit, avant de calculer l’aire de l’ellipse

(6.64)

et (6.65)

où q = arctan(-b) et b est la pente de l’axe principal de ellipse.

La deuxième méthode, beaucoup plus simple, qui permet de déterminer s_x et s_y corrigés pour l’orientation de l’ellipse, fait appel aux valeurs propres de la matrice des variances-covariances dérivées des coordonnées des observations. Puisque ces valeurs propres sont analogues à des variances, leurs racines carrées fournissent aussi des valeurs équivalentes aux écarts-types des données géographiques transformées (c’est à dire, et ). Bien que cette seconde procédure soit beaucoup plus simple, les transformations trigonométriques de points individuels des données sont également utiles à plusieurs égards, comme le verrons plus loin.

Le fait de prendre l’ellipse type comme mesure du domaine vital pose un autre problème  car les variances et covariances utilisées dans les calculs sont des estimations de valeurs paramétriques. En tant que telles, elles sont influencées par la taille de l’échantillon. A partir du moment où les données suivent une loi de distribution normale à deux variables, l’incorporation du critère de test statistique F dans le calcul de l’ellipse permet de compenser en partie la taille de l’échantillon. La formule,

(6.66)

peut être utilisée pour éliminer l’incidence de la taille de l’échantillon qui a servi à déterminer ce qui est maintenant devenu une ellipse d’un pourcentage de confiance de [(1-a )100]. Cette mesure est supposée fournir une estimation fiable de la taille du domaine vital, lorsque les données géographiques suivent une loi de distribution normale à deux variables. Avant l’introduction du test F, les calculs présentés pourraient s’appliquer à tous les cas où l’éparpillement des données géographiques est symétrique, unimodal. White et Garrott (1990) ont indiqué les calculs supplémentaires qui doivent être faits pour tracer sur papier l’ellipse de confiance [(1-a )100].

L’application d’un modèle général du domaine vital permet de tirer des conclusions sur la familiarité relative d’un animal avec un point quelconque situé à l’intérieur de son domaine vital. Ces informations peuvent être déterminées avec plus de précision par une simple observation, mais elles sont extrêmement coûteuses, en temps, et il est difficile de faire des comparaisons quantitatives entre des individus ou entre des enquêtes. A propos du concept de centre d’activité, Hayne (1949) estime que, bien qu’il soit tentant d’identifier le centre d’activité avec l’emplacement du domaine vital d’un animal, cela ne doit pas être fait car ce point est une moyenne des points de capture et n’a pas nécessairement d’autre signification biologique. Mis à part le problème que nous venons de mentionner, les écarts inhérents à la normalité des données géographiques peuvent être une source de difficultés. Du fait de l’étalement (asymétrie du domaine vital), le centre d’activité se trouve en réalité plus près d’un arc de l’ellipse de confiance que ne le prévoyait le modèle, de sorte que la taille du domaine vital (l’ellipse de confiance [1-a ]100 ) est surestimée. La kurtose (aplatissement) peut augmenter ou diminuer les estimations de la taille du domaine vital. Si les données sont platikurtiques, la taille du domaine vital est sous-évaluée, et inversement dans le cas de données leptokurtiques. La transformation trigonométrique de données à deux variables aide à résoudre ce problème en fournissant des distributions non-corrélées des coordonnées x et y. Quoiqu’il en soit, pour vérifier le bien-fondé de l’hypothèse de la distribution normale à deux variables, on peut se référer aux méthodes décrites par White et Garrott (1990), que nous ne développerons pas ici pour ne pas compliquer notre exposé.

La taille de l’échantillon peut avoir une influence importante sur la fiabilité des statistiques présentées ici. Il est assez évident que les petites tailles d’échantillons (ex : n <20), peuvent fausser sérieusement les mesures considérées. Une multitude de facteurs qui n’ont pas été pris en considération dans cette étude, peuvent également influencer les résultats sans que l’on sache encore comment. C’est notamment le cas des différences entre les espèces et les individus, du comportement social, des sources de nourriture et de l’hétérogénéité de l’habitat, pour n’en citer que quelques-uns.

Les étapes du calcul du domaine vital sont décrites ci-après, à partir de données simulées obéissant à une loi de distribution normale à deux variables avec m _x = m _y = 10, s _x = s _y = 3, et cov (x,y) = 0 (White and Garrott (1990)). Ces données sont reportées dans le Tableau 6.23.

Tableau 6.23. Données simulées obéissants à une loi de distribution normale à deux variables avec m _x = m _y = 10, s _x = s _y = 3, et cov (x,y) = 0.

*Etape 1. Calcul des moyennes, des variances et des covariances

= 10.14

=10.35

=11.78

= 2.57

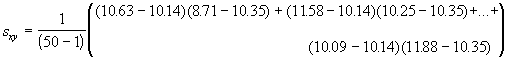= -1.22

= 3.43

= 1.60

*Etape 2. Calcul des valeurs propres et des pentes des axes.

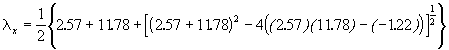
= 11.6434

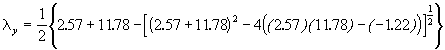
= 2.7076

*Etape 3. Calcul des valeurs de et .

= = 3.4122

= = 1.6455

*Etape 4. Calcul du domaine vital sur la base du test F à (1-a ) = 0.95.

.

=

= 114.8118 m² = 0.0115 ha