CAPÍTULO 2 – MODELOS Y TASAS

2.1 Modelos

La ciencia construye modelos o teorías para explicar fenómenos. Los fenómenos son observados y se establecen relaciones, causas y explicaciones. Las observaciones se realizan sobre la evolución de magnitudes (características) con el tiempo (o con otras características) y tomando en consideración sus posibles causas (factores).

• Física – fenómeno del movimiento de los cuerpos (características – espacios recorridos en relación a los tiempos invertidos en recorrerlos)

• Biología – fenómeno del crecimiento (característica – talla, o peso, en relación al tiempo)

2.1.1 ESTRUCTURA DE UN MODELO

Suposiciones básicas

• simplifican la realidad

• deben ser simples y «tratables» matemáticamente

• no pueden ser contradictorias

• no se demuestran

• se establecen sobre características

Las suposiciones básicas, normalmente, se refieren a la evolución de las características y se establecen sobre las tasas de variación de esas características.

Relaciones (propiedades)

• se deducen de las suposiciones básicas, o de relaciones deducidas anteriormente mediante leyes de la lógica (matemática). Las propiedades también llamadas:

«resultados» o «conclusiones» del modelo

Verificación

• los resultados del modelo deben ser coherentes (concordar) con la realidad.

la verificación implica observación (práctica):

muestreo, métodos estadísticos,...

Perfeccionamiento

• si los resultados no concuerdan con la realidad se deben modificar las suposiciones básicas.

• si la concordancia es aproximada se debe valorar si la aproximación es suficiente o no.

• la modificación de las suposiciones básicas puede consistir simplemente en «ampliar el ámbito» de la realidad que sirvió de base para las suposiciones, para adaptarlas a la nueva realidad sobre la cual se pretende aplicar el modelo.

Ventajas

• es más sencillo analizar las propiedades del modelo que la realidad

• resultados útiles en la práctica

• posibilidad de analizar situaciones o escenarios diferentes

• destacar lo esencial de los fenómenos y sus causas

• posibilidad de perfeccionamiento

2.1.2 TIPOS DE MODELOS MÁS USADOS EN LA EVALUACIÓN PESQUERA

Modelos de Producción

Los modelos de producción, también llamados modelos de Producción General, modelos Globales, modelos Sintéticos o incluso modelos del tipo Lotka-Volterra. Estos modelos consideran el stock en su globalidad, en particular la abundancia total (en peso o en número) y estudian su evolución, los efectos del esfuerzo de pesca, etc. No consideran la estructura de edades o de tamaños del stock.

Modelos Estructurales

Estos modelos consideran la estructura de edades del stock y la evolución de esa estructura con el tiempo. Pero, principalmente, se basan en que el stock, en un período determinado de tiempo, esta formado por individuos de diferentes cohortes, y por lo tanto de diferentes edades y tamaños. De este modo, permiten análisis y previsiones de lo que le puede acontecer al stock y a las capturas, basándose en la evolución de las diferentes cohortes que lo componen.

En este manual no se seguirá el camino histórico de la construcción de los modelos. Se ha considerado más conveniente discutir en primer lugar los Modelos Estructurales y posteriormente analizar los Modelos de Producción.

2.2 Tasas

Las suposiciones básicas de un modelo de la evolución de una característica precisan del concepto de tasa de variación de la característica en relación al tiempo (o a otras características).

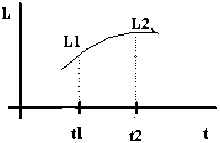
Figura 2.1 Evolución de la talla (L) de un individuo con el tiempo (o la edad) (t)

Para el estudio general de tasas, se substituye la característica L del ejemplo por y, y la variable asociada no será el tiempo t sino la variable x. Pensando en los modelos de evaluación y con el fin de simplificar, se considera que la función y, solo toma valores reales y no negativos.

2.2.1 TASA MEDIA ABSOLUTA – tma(y)

Se considera y una función de x y el intervalo i de limites (x_i, x_i+1)

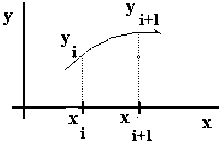
Figura 2.2 Función y=f(x) al variar en el intervalo i

Sean:

Dx_i = x_i+1 - x_i el tamaño del intervalo

y_i = valor de y cuando x = x_i

y_i+1 = valor de y cuando x = x_i+1

La variación de y en el intervalo Dx_i será Dy_i = y_i+1 – y_i

La tasa media absoluta, tma(y), de la variación de y en el intervalo Dx_i será:

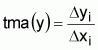
Gráficamente:

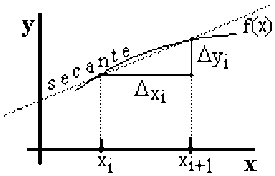
Figura 2.3 Tasa media absoluta de variación de y en el intervalo Dx_i

pendiente de la secante =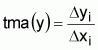

= tma(y) durante Dxi

Nota: tma(y) es conocida en la física como velocidad media de variación de y respecto a x, en el intervalo Dx_i.

2.2.2 TASA INSTANTANEA ABSOLUTA – tia(y)

Sea y una función de x

La tasa instantánea absoluta de y en el punto x = x_i es la derivada de y con respecto a x en ese punto.

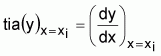
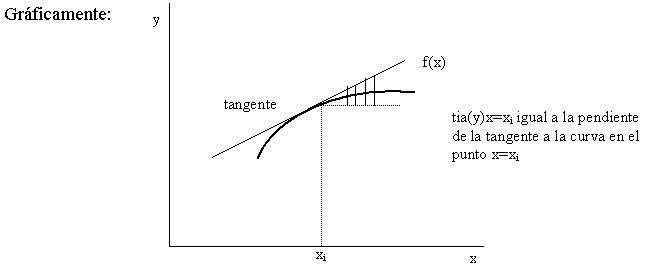
Figura 2.4 Tasa instantánea absoluta de y en el punto x_i

Nota: tia(y) es conocida como velocidad instantánea de variación de y con x en el punto x.

Propiedades

1. Dada la tia(y) el cálculo de la función y se obtiene, por integración, siendo

y = f(x) + Constante, donde f(x) = Primitiva de tia(y) y la Constante es la constante de integración.

Si aceptamos una condición inicial x^*, y^*, donde y^* es el valor de y correspondiente a x = x^*, eliminando la Constante, resulta y = y^*+f(x)-f(x^*)

2. El ángulo que forma la tangente a la curva y con el eje de las x es la inclinación.

- La tangente trigonométrica de la inclinación es la pendiente de la tangente geométrica.

- tia(y) = derivada de y = pendiente = tg (inclinación)

3. Si en un punto x cumple:

tia(y) > 0 entonces y es creciente en ese punto

tia(y) < 0 entonces y es decreciente

tia(y) = 0 entonces y es estacionaria en ese punto (máximo o mínimo)

4. Si tia(y) = constante = const entonces y es función lineal de x, o según la propiedad 1 (ver pagina 11) será:

5. Si y(x) = u(x) + v(x) entonces tia(y) = tia(u) + tia(v)

6. Si las causas A y B provocan aisladamente variaciones en y entonces las causas A y B simultáneamente provocaran una variación en y tal que

tia(y) _total = tia(y) _{causa A} + tia(y) _{causa B}

tia(tia(y)) = d²y/dx² = aceleración de y en el punto x

7. Si la aceleración en el punto x es positiva entonces la tia(y) es creciente y si aquella aceleración es negativa la tia(y) será decreciente.

2.2.3 TASA MEDIA RELATIVA – tmr(y)

Se considera y una función de x y el intervalo (x_i, x_i+1)

Sean:

Dx_i = x_i+1- x_i = tamaño del intervalo

y_i = valor de y cuando x = x_i

y_i+1 = valor de y cuando x = x_i+1

x_i* = cierto punto del intervalo (x_i, x_i+1)

y_i* = valor de y cuando x = x_i*

x_i^* puede ser x_i, x_i+1, , etc.

La tasa media de y relativa a y_i* será:

o

Comentarios

1. tmr(y) está asociada con la tasa media de variación porcentual de y en relación a la media y*, esto es,

2. Se considera = x_i + Dx_i/2 = 1/2 . (x_i,+ x_i+1) =

3. Por lo cual, entonces, se llamara en el intervalo (x_i, x_i+1) al valor de y cuando

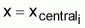
Nótese que puede ser diferente de la media, (y_i + y_i+1)/2

4. Es frecuente calcular tmr(y) en relación a del intervalo.

2.2.4 TASA INSTANTANEA RELATIVA – tir(y)

Sea y una función de x

La tasa instantánea relativa de y en el punto x = x_i es

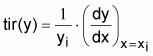o

Propiedades

1. Dada la tir(y), el cálculo de la función y se obtiene por integración, siendo y = f(x) + Constante, donde f(x) = Primitiva de tir(y) y Constante es la constante de integración.

Si se adopta la condición inicial x^*, y^*, donde y^* es el valor de y correspondiente a x = x^*, tenemos, eliminando la Constante, y = y^*+ f(x) - f(x^*)

2. Si en un punto x se da:

tir(y) > 0 entonces y es creciente en ese punto

tir(y) < 0 entonces y es decreciente

tir(y) = 0 entonces y es estacionario en ese punto (máximo o mínimo)

3. tir(y) = tia(lny) como se deduce de las reglas de la derivación

4. Si tir(y)= constante = const. entonces y es función exponencial de x, esto es,

y = Constante.e^const.x o

y = y* . e^{const.(x - x*)} y vice-versa.

5. Si y(x) = u(x).v(x) entonces tir(y) = tir(u) + tir(v)

6. Si las causas A y B provocan aisladamente variaciones en y entonces las causas A y B simultáneamente provocaran una variación en y tal que

tir(y)_total = tir(y)_{causa A} + tir(y)_{causa B}

2.3 Modelo lineal simple

Sea y = f(x)

Suposición básica del modelo

tia(y) = Constante = b en el intervalo (x_i, x_i+1): Dx_i = x_i+1 – x_i

Condición inicial

x* = x_i Þ y* = y_i

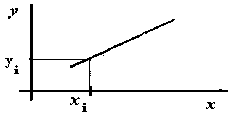
Figura 2.5 Representación gráfica de un modelo lineal simple

Propiedades

Otras expresiones útiles

Demostraciones más importantes

2.4 Modelo exponencial

Sea

Suposición básica del modelo

tir(y) = Constante = c en el intervalo

Condición inicial

x* = x_i Þ y* = y_i

Propiedades

Considerando que tir(y) = tia(lny) se puede decir que el modelo exponencial de y contra x es equivalente al modelo lineal de lny contra x. Así, sus propiedades más importantes pueden deducirse tomando antilogaritmos a las propiedades del modelo lineal de lny contra x.

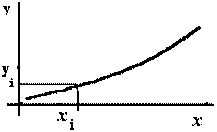
Figura 2.6 Representación gráfica del modelo exponencial

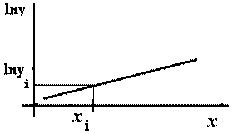
Figura 2.7 Representación gráfica del modelo lineal de lny contra x

Otras expresiones útiles

Demostraciones