8. LEVANTAMIENTOS TOPOGRÁFICOS � NIVELACIÓN DIRECTA
8.0 Introducción
|
| 1. En los capítulos 5 y 6 del Volumen 1 de este Manual,
se han ilustrado varios dispositivos para medir diferencias de altura. También
se enseñó cómo usar tales dispositivos
para resolver tres tipos
de problemas, que se presentan cuando se miden diferencias de altura
en el curso del diseño y la realización de una granja acuícola
(ver Sección 50). Ahora es posible aprender cómo planificar
un levantamiento para resolver tales problemas, cómo llevar
el registro de las mediciones realizadas en el cuaderno de campo y
cómo encontrar la información necesaria a partir
de dichas mediciones. |
|
|
| |
|
|
Altura y altitud de un punto
|
| 2. Ya se ha visto qué es la altura de un punto
del suelo. De todos modos, es importante formular una definición
más precisa de esos términos.
- Cuando la altura de un punto es su distancia vertical por encima
o por debajo de la superficie de un plano de referencia elegido,
hablamos de la altura* de ese punto.
- Cuando la altura de un punto es su distancia vertical por encima
o por debajo del nivel del mar (como plano de referencia), se
trata de la altitud* del punto.
|
Ejemplo
|
|
Altura del punto por encima de la marca A, sobre
el suelo
Altitud del mismo punto sobre el nivel del mar (asnm) |
1.83 m
345 m
|
3. La distancia vertical entre dos puntos se llama diferencia de
nivel, un concepto similar al definido antes como diferencia de
altura (ver Sección 50). La medición de las diferencias
de nivel se llama nivelación y constituye una operación
básica en los levantamientos topográficos.
|
|
|
| |
|
|
|
¿Cuáles son los principales métodos de nivelación?
|
|
4. Es posible utilizar diferentes métodos de nivelación,
tales como:
- nivelación directa, que comporta la medición
directa de las diferencias de nivel; se trata del método usado
más frecuentemente;
- nivelación indirecta, que comporta el cálculo
de las diferencias de altura a partir de las pendientes y distancias
horizontales medidas.
|
|
Nivelaci�n directa

|
| |
|
|
|
Ya se ha visto qué es la nivelación indirecta en la Sección
50, cuando se enseñó calcular
las diferencias de nivel a partir de pendientes o �ngulos
verticales. A continuación se estudia en qué consiste
la nivelación directa.

|
|
Nivelaci�n indirecta

|
¿Cuáles son los distintos tipos de nivelación directa?
5. La nivelación directa permite medir ya sea la altura de los puntos,
como la diferencia de nivel entre diversos puntos mediante un nivel y una mira
graduada (ver Capítulo 5). Existen dos tipos de nivelación directa:
- la nivelación diferencial; y
- la nivelación de perfiles.
6.Cuando se lleva a cabo una nivelación directa, se determina
la diferencia de nivel de puntos que están a una cierta distancia unos
de otros (ver Sección 81). La nivelación directa más sencilla
consiste en medir sólo dos puntos, A y B, a partir de una estación
central, EN. Pero también puede ser necesario determinar la diferencia
de nivel entre:
- varios puntos A, B, ... E, observados desde una sola estación de
nivelación, EN; o
- varios puntos A, ... F, observados desde una serie de estaciones de nivelación,
EN1, ... EN6, por ejemplo.
7. Cuando se lleva a cabo una nivelación de perfil, se determina
el nivel o cota de puntos situados a intervalos regulares a lo largo de una
línea conocida, tal como el eje de un canal de alimentación de
agua o el eje longitudinal de un valle. Este tipo de nivelación permite
determinar la altura de diferentes puntos de un perfil transversal
(ver Sección 8.2).
8. También se puede usar la nivelación directa para determinar
las alturas necesarias para el trazado de curvas de nivel (ver Sección
8.3), y l�neas de pendiente constante (ver Secci�n
6.9), en cuyo caso se combina la nivelación diferencial y la nivelación
de perfiles.
|
Nivelaci�n diferencial

|
|
Nivelaci�n de perfil

|
9. Existen varios modos sencillos para determinar la altura de puntos del
suelo y las diferencias de nivel entre ellos; y en todos estos casos se usan
un nivel y una mira graduada. En las secciones siguientes se describen detalladamente
estos métodos, para ayudar a decidir cuál se debe usar. El Cuadro
10 permite comparar los varios métodos y seleccionar el que mejor
se adecua a cada necesidad, en cada situación.
| CUADRO
10
M�todos de nivelaci�n directa
|
Secci�n
|
Tipo
|
M�todo
|
Aplicabilidad
|
Comentarios
|
|
|
Nivelación diferencial
|
Poligonal abierta
|
Extensión de tierra larga y estrecha
|
Verificar el error de cierre
|
|
|
Nivelación diferencial
|
Poligonal cerrada
|
Perímetro de la parcela de tierra y
línea de base para la proyección radial
|
Verificar el error de cierreCombinar con el
método radial
|
|
|
Nivelación diferencial
|
Cuadrículas
|
Parcela de tierra con poca vegetación
|
Cuadrados de 10 a 20 m y de 30 a 50 m
|
|
|
Nivelación diferencial
|
Radial
|
Parcela grande con visibilidad
|
Combinar con poligonal cerrada
|
|
|
Nivelación del perfil longitudinal
|
Poligonal abierta
|
Niveles con visor y sin visor
|
Verificar el error de cierre
|
|
|
Nivelación del corte transversal
|
Radial
|
Nivel con visor y buena visibilidad
|
|
|
|
Curvas de nivel
|
Directo
|
Realización de mapas de áreas
pequeñas con niveles con y sin visor y miras de plancheta
|
Lento y preciso
Proceder de abajo hacia arriba
|
|
|
Curvas de nivel
|
Cuadrículas
|
Parcelas pequeñas con poca vegetación
Especialmente si ya se ha hecho el levantamiento del perímetroMapas
a pequeña y mediana escala
|
El terreno, la escala y la precisión
dependen del intervalo entre las curvas de nivel. Proceder
de abajo hacia arribaAdecuado para el uso de la plancheta
|
|
|
Curvas de nivel
|
Radial
|
Mapas de grandes áreas a pequeña
y mediana escala
|
Rápido y algo imprecisoProceder de
abajo hacia arribaAdecuado para el uso de la plancheta
|
|
|
Curvas de nivel
|
Secciones transversales
|
Levantamiento preliminar de extensiones de
tierra largas y estrechas
|
Rápido y algo imprecisoProceder de
abajo hacia arribaAdecuado para el uso de la plancheta
|
|
8.1
Cómo realizar un levantamiento topográfico por nivelación
diferencial
|
¿Qué es el levantamiento diferencial?
|
| 1. Para comprender cabalmente qué se entiende por
nivelación diferencial, es preferible partir de una situación
en la cual se toman en cuenta sólo dos puntos, A y B,
ambos visibles desde una estación central de nivelación,
EN. .
- Desde EN, mire hacia una mira graduada colocada en el punto A. El
punto de intersección de la línea visual con la mira graduada,
es el punto X. Mida AX. Esta operación se llama visual hacia
atrás (VAt).
|
|
Halle AX por visual hacia atr�s

|
| |
|
|
- Gire, y desde EN mire hacia la mira graduada colocada en el punto
B. El punto de intersección de la línea visual con la
mira graduada, es el punto Y. Mida BY. En este caso la operación
se llama visual hacia adelante (VAd).
|
|
Halle BY por una visual hacia adelante

|
| |
|
|
- La diferencia de nivel entre los puntos A y B es igual
a BC o (AX � BY) o (visual hacia atrás VAt � visual
hacia adelante VAd).
|
|
La diferencia de altura entre
los puntos A y B es igual a AX menos BY

|
| |
|
|
|
- Si se conoce la altura de A, llamada H(A), se puede calcular la
altura de B, llamada H(B), como VAt � VAd
+ H(A).
- Pero VAt + H(A) = HI, la altura del instrumento o la altura de
la línea visual dirigida desde el nivel.
|
|
|
| |
|
|
(la altura del punto B es igual a la altura del instrumento de nivelación,
menos la visual hacia adelante).
|
|
|
¿Qué son visual hacia atrás y visual hacia
adelante?
|
| Es importante entender qué son exactamente la �visual
hacia atrás� y la �visual hacia adelante�, en
nivelación directa.
2. Una visual hacia atrás (VAt)
es la visual efectuada con el nivel hacia un punto de altura conocida
H, de tal modo que se puede determinar la altura del instrumento
HI. En nivelación directa, la visual hacia atrás se efectúa
comúnmente mirando hacia atrás, pero no siempre es así.
Las visuales hacia atrás también se llaman visuales
directas (+V), porque siempre se las debe sumar a una altura conocida
para determinar HI.
|
|
|
| |
|
|
| 3.Una visual hacia adelante (VAd)
también es la visual efectuada con un nivel, pero se puede dirigir
a cualquier punto de la línea visual sobre la cual se debe determinar
la altura. La visual hacia adelante comúnmente se realiza mirando
hacia adelante, pero no siempre. Las visuales hacia adelante también
se llaman visuales inversas (-V), porque siempre se las sustrae
de la HI para hallar la altura A del punto. Recuerde que:
|
|
|
| |
|
|
Levantamiento de dos puntos desde un
punto intermedio
|
| 4. A menudo es imposible observar simultáneamente los
dos puntos objeto de la medición, o también puede ocurrir
que estén muy alejados. En tales casos, es necesario realizar series
de nivelaciones diferenciales. Se trata de una operación similar
a la descrita arriba, excepto porque se usan puntos intermedios provisionales
llamados puntos intermedios (PI). |
|
|
| |
|
|
| 5. Se conoce la altura del punto A, H(A) = 100 m y se quiere
hallar la altura del punto B, H(B), que no es visible desde la estación
central de nivelación. Se elige un punto intermedio C
más o menos a mitad de camino entre A y B. Se determina el nivel
de EN1, a mitad de camino entre A y C. |
|
|
| |
|
|
| 6. Efectúe una visual hacia atrás desde A (por
ejemplo VAt = 1,89 m). Mida la visual hacia adelante en C, VAd = 0,72m.
Calcule HI = VAt + H(A) = 1,89 m + 100 m = 101,89 m. Halle la altura del
punto intermedio C como H(C) = HI � VAd = 101,89 m � 0,72 m =
101,17 m. |
|
|
| |
|
|
| |
|
|
|
7. Diríjase a una segunda estación de nivelación,
EN2, más o menos equidistante a C y B. Determine el nivel y mida
VAt = 1,96 m, y luego VAd = 0,87 m. Calcule HI = VAt + A(C)
= 1,96 m + 101,17 m = 103,13 m. Halle H(B) = HI � VAd = 103,13 m � 0,87
m = 102,26 m.
8. El cálculo se realiza con mayor facilidad si se registran
las mediciones de campo en un cuadro, tal como se muestra en el
ejemplo. No es necesario efectuar cálculos intermedios. Todas las
VAt y las VAd se suman separadamente. La suma VAd se resta de la suma
VAt para hallar la diferencia de altura desde el punto A al B. A to point
B.
- Una diferencia positiva significa que B está a
una altura superior que A.
- Una diferencia negativa significa que B está a
una altura inferior que A.
|
|
|
| |
|
|
|
Conociendo la altura de A, a continuación es posible calcular
fácilmente la altura de B. En este caso, H(B) = 100 m + 2,26 m
= 102,26 m; que es el mismo resultado alcanzado en el punto 7, pero que
requiere cálculos mucho más complicados. Este tipo de cálculo
se llama verificación aritmética.
Ejemplo
Cuadro tipo para la nivelación diferencial con un punto intermedio.

|
|
|
Levantamiento de dos puntos con varios puntos intermedios
9. A menudo es necesario usar más de un punto intermedio entre un punto
de altura conocida y otro, cuya altura se desconoce. A tal efecto, se puede
usar el procedimiento apenas explicado, pero hará falta registrar
las mediciones de campo en un cuadro para facilitar el cálculo.
10. Conociendo la altura del punto A, necesita hallar la altura de B. A tal
efecto, son necesarios cinco puntos intermedios, PI1 ... PI5, y seis
estaciones de nivelación, EN1 ... EN6.
Nota : los puntos intermedios y las estaciones de nivelación
no es necesario que estén sobre la misma línea recta, pero es
importante colocar cada estación de nivelación aproximadamente
equidistante de los dos puntos que se quieren medir desde esa estación.
11. Desde cada estación de nivelación, haga una visual hacia
atrás (VAt) y una visual hacia adelante (VAd), excepto:
- en el punto de partida A, donde se efectúa sólo
una visual hacia atrás; o
- en el punto de llegada B, donde se efectúa sólo
una visual hacia adelante.
|

|
| |
|
Ejemplo
Cuadro tipo para la nivelaci�n diferencial con varios puntos intermedios

|
Utilizando el punto 8 como guía, registre todas las mediciones en un
cuadro y calcule el resultado. Habrá determinado que el punto B es 2,82
m más alto que el punto A, y que por lo tanto, su altura es H(B) = 100
m + 2,82 m = 102,82 m.
12. Aun cuando se proceda con cuidado, es posible cometer errores cuando se
realizan cálculos aritméticos a partir de las cifras registradas.
Para reducir ese margen de error, agregue dos columnas adicionales
al cuadro para facilitar la verificación. En esas columnas, anote la
diferencia (VAt � VAd), ya sea positiva (+), o negativa (�) entre las medidas
efectuadas en cada estación de nivelación. Por ejemplo, a partir
de la EN1 se ha medido VAt(A) = 1,50 m y VAd (PI1) = 1,00 m. La diferencia 1,50
m � 1,00 m = 0,50 m es positiva, por lo tanto se anota en la columna (+) en
la línea PI1.
La suma aritmética de tales diferencias debe ser igual a
la diferencia de nivel calculada D(H) = +2,82 m. Dichas columnas ayudan además
a calcular la altura de cada punto intermedio y a verificar mejor
la altura del punto B.
| Ejemplo
Nivelaci�n diferencial con varios puntos intermedios
|
|
Realizaci�n de un levantamiento topogr�fico por poligonal abierta rectil�nea
|
|
13. Los conocimientos adquiridos hasta ahora permiten llevar a cabo el
levantamiento topográfico de dos puntos distantes, midiendo la
distancia horizontal entre ellos y su diferencia de nivel.
Para realizar el levantamiento topográfico del emplazamiento de
una granja acuícola, se utiliza un método muy semejante.
Se prepara el mapa topográfico del sitio (ver Capítulo 9)
que es una guía útil para el diseño de la granja.
14. Este método topográfico utiliza poligonales abiertas
rectilíneas, o sea que comportan varias estaciones intermedias
ubicadas a lo largo de una línea recta. Se conoce la altura del
punto inicial A, H(A) = 63,55 m. Se quiere hallar la distancia que separa
el punto B del punto A, y sus niveles. Dada la naturaleza del terreno
en el cual se trabaja, es imposible ver el punto B desde el punto A, por
lo cual se necesitan dos puntos intermedios, PI1 y PI2, para
la nivelación. Mida las distancias horizontales a medida que avanza
con el nivel, desde el punto A hacia el B; trate de mantener la línea
recta. Si no es posible, debe usar el levantamiento por poligonal
abierta quebrada, que comporta la medición de los azimut
de cada sección de poligonal a medida que avanza y cambia de dirección
(ver punto 17).
|
|
|
15. Prepare un cuadro como el descrito en el punto 12
y agregue dos columnas para las distancias horizontales. Anote todas las mediciones
de distancia y altura en la parte principal del cuadro. Luego, en la primera
columna adicional, registre cada distancia parcial medida desde un
punto al siguiente. En la segunda columna, anote la distancia acumulada,
que es la distancia calculada desde el punto inicial A hasta el punto en el
cual usted se encuentra midiendo. La última cifra de la segunda columna
será la distancia total AB.
| Ejemplo
Levantamiento topográfico de una poligonal abierta rectilínea
por nivelación diferencial
 |
16. Conclusiones. El punto B está situado a un
nivel de 1,55 m por encima del punto A, su altura es 65,10 m y dista 156,50
m del punto A. La verificación aritmética de las diferencias (VAt
� VAd) coincide con las diferencias de nivel calculadas.
Levantamientos topográficos por poligonales abiertas
de línea quebrada
|
| 17. Recuerde que si realiza un levantamiento por poligonal
abierta de línea quebrada (o en zigzag), también es necesario
medir el azimut de cada secci�n de poligonal a medida que
avanza, además de las distancias y las alturas. |
|
|
| |
|
|
| 18. Se debe realizar el levantamiento de la poligonal
abierta ABCDE a partir del punto conocido A. Son necesarios cuatro puntos
intermedios, PI1, PI2, PI3 y PI4. Se quiere hallar:
- las alturas de los puntos B, C, D y E;
- las distancias horizontales entre tales puntos;
- la posición de cada punto en relación a los otros,
de manera que se pueda preparar un mapa topográfico.
|
|
|
| |
|
|
|
|
| Proceda por nivelación diferencial siguiendo las indicaciones
precedentes, efectuando mediciones de visuales hacia adelante y hacia
atrás desde cada estación de nivelación. Mida
los azimut y las distancias horizontales a medida que avanza a partir del
punto conocido A, hacia el punto final E. Todos los azimut de los puntos
intermedios situados sobre una misma rectas son iguales, lo cual facilita
la verificación del trabajo. |
|
|
| |
|
|
| 19. Prepare un cuadro semejante al que se ilustra
en el punto 15 y agregue tres columnas adicionales para anotar
y verificar los valores de los azimut (ver Sección 71,
punto 17). Anote todas las mediciones en ese cuadro. En la parte de abajo,
realice todas las verificaciones de los cálculos de altura, tal como
ha aprendido en los puntos precedentes. |
|
|
| |
|
|
|
Ejemplo
Levantamiento topogr�fico por nivelaci�n diferencial de una poligonal abierta y quebrada

|
Verificación de los errores de nivelación
|
| 20. El hecho de verificar los cálculos aritméticos
no dice mucho sobre la precisión del levantamiento realizado. Para
verificar la precisión de las operaciones efectuadas, se debe llevar
a cabo la nivelación en sentido inverso, desde el punto
final hacia el inicial, utilizando el mismo procedimiento. Es probable que
la altura del punto A que se obtiene mediante la segunda nivelación,
sea diferente de la altura conocida. Esa diferencia es el error de
cierre. |
|
|
| |
|
|
|
Ejemplo
A partir del punto A de altura conocida, realice un levantamiento
por poligonal a través de cinco puntos intermedios, PI1 ... PI5
y determine la altura del punto B. Para verificar el error de cierre,
haga el levantamiento por poligonal de la recta BA, con otros cuatro puntos
intermedios PI6 ... PI9 y calcule a continuación la altura del
punto A. Si la altura conocida de ese punto de partida A es 153 m y si
la altura calculada de A, al final del levantamiento, es de 153,2 m, el
error de cierre es entonces igual a 153,2 m � 153 m = 0,2 m..
|
|
|
| |
|
|
| |
|
|
21. El error de cierre debe ser inferior al error admisible, que es el límite
de error que se puede dar en un levantamiento considerado preciso. El tamaño
del error admisible depende del tipo de levantamiento (prospección, preliminar,
detallado, etc.) y de la distancia total recorrida durante el levantamiento.
Como una ayuda para determinar la precisión de cada levantamiento, se
puede calcular el error máximo admisible (EMA) expresado en centímetros,
de la siguiente manera:
| Prospección y levantamiento preliminar
EMA (cm) = 10 √D
La mayoría de los levantamientos de ingeniería
EMA (cm) = 2,5 √D |
donde D es la distancia total recorrida durante el levantamiento,
expresada en kilómetros.
Ejemplo
Se acaba de completar una prospecci�n. El error de cierre es de 0,2 m o 20 cm, al final de la poligonal de 2,5 km + 1,8 km = 4,3 km de largo. En este caso, el m�ximo error admisible (en cent�metros) equivale a 10�4.3
= 10 x 2.07 = 20.7 cm. Dado que el error de cierre es inferior al EMA, las mediciones han sido lo suficientemente precisas para una prospecci�n.
Levantamientos topográficos
por poligonales cerradas
|
| 22. En la sección precedente se ha llevado a cabo un
levantamiento topográfico de poligonal abierta uniendo los puntos
A y B. Es posible realizar el levantamiento de una poligonal cerrada,
tal como el perímetro del terreno de una granja piscícola,
de una manera similar. Se deben usar los vértices del perímetro
A, B, C, D, E y F como puntos de nivelación y establecer entre
ellos tantos puntos intermedios como sea necesario. Realice
el levantamiento planim�trico como se explica en la Secci�n 7.1, y utilice
la nivelación diferencial para determinar la altura de cada punto
del perímetro.
23. Si no se conoce la altura exacta del punto inicial A, se le puede
dar un valor cualquiera, por ejemplo H(A) = 100 m. Comience el levantamiento
en el punto A y proceda en la dirección de las agujas del
reloj, siguiendo el perímetro del área. Realice mediciones
colocando la mira graduada en los puntos PI1, PI2, B, PI3, etc., hasta
regresar al punto inicial A y cerrar la poligonal. Simultáneamente,
lleve a cabo las mediciones de distancias horizontales y azimut, que sean
necesarios. Registre el resultado de las lecturas en dos cuadros
distintos, el primero para el levantamiento planimétrico
y el segundo para la nivelación; o también en un solo
cuadro que incluya las medidas de distancia. Utilizando las columnas
(VAt � VAd) es fácil determinar la altura de cada punto a partir
de la altura conocida (o supuesta) del punto A. Verifique todos
los cálculos, tal como se ha indicado en los puntos 15 y 16. Determine
a continuación el error de nivelación de cierre en el punto
A (ver punto 20). Tal error debe ser inferior o igual al error máximo
admisible (ver punto 21). |
|
|
| |
|
|
|
Ejemplo
Levantamiento topogr�fico de una poligonal cerrada por nivelaci�n diferencial

|
|
Levantamiento topográfico
por cuadrícula
|
|
|
| 24. El método de la cuadrícula es especialmente
útil para llevar a cabo el levantamiento de terrenos pequeños
con poca vegetación. En áreas más grandes, con vegetación
alta o bosques, el método resulta más difícil de
usar y poco práctico. Su aplicación consiste en determinar
cuadrados en el área objeto del levantamiento, y la altura de los
ángulos de dichos cuadrados.
25. El tamaño de los cuadrados trazados depende de
la precisión que se requiere. Para una mayor precisión,
los lados de los cuadrados deben medir de 10 a 20 m de longitud. En el
caso de prospecciones que requieren menos precisión, los lados
de los cuadrados pueden medir de 30 a 50 m. |
|
|
| |
|
|
| 26. Seleccione la línea base AA sobre el
terreno y márquela claramente con jalones. Esa línea de base
debe estar preferiblemente, situada al centro del lugar y paralela
a los costados más largos. Si utiliza una brújula, es preferible
orientar la línea base en la dirección norte-sur.
27. Trabajando cuesta arriba, encadene la línea de base a partir
del perímetro del área y coloque jalones a intervalos
regulares, que sean iguales a la medida del costado de los cuadrados que
se ha seleccionado, por ejemplo 20 m. Numere visiblemente dichos jalones,
1, 2, 3 ... |
|
|
| |
|
|
| 28. A partir de cada jalón, trace una línea
recta perpendicular a la l�nea de base , que atraviese
toda la superficie del terreno. |
|
|
29. Encadene toda la longitud de cada
perpendicular, a cada lado de la l�nea base. Coloque un jalón
cada 20 m (la medida del cuadrado elegida). Identifique cada jalón
con:
- una letra (A, B, C, etc.) que se refiere a la línea
paralela a la línea base, sobre la cual se encuentra el punto
en cuestión;
- un número (1,2,3, ... n) que se refiere a la perpendicular,
trazada a partir de la línea base, a la cual el punto pertenece.
Ejemplo
A 20 m del punto A1, la perpendicular 2 corta la recta AA en el
punto A2.
El punto B2 se encuentra 20 m a la izquierda del punto A2,
sobre la recta BB.. |
|
|
| |
|
|
| 30. Una vez trazada la cuadrícula sobre
el terreno, es necesario determinar la altura de los ángulos
de los cuadrados, marcados con los jalones. En primer lugar instale un punto fijo de referencia (PF) sobre
la línea base AA cerca del límite del área
y preferiblemente en la parte más baja (ver punto 42-44). El punto
fijo de referencia se puede establecer en un sitio de altura conocida
(tal como el punto de una poligonal cuyo levantamiento se ha realizado
precedentemente) o también en un punto de altura supuesta
(por ejemplo, 100 m) (ver punto 45).
31. Se realiza el levantamiento de los puntos de la cuadrícula,
en dos etapas.
|
|
|
| |
|
|
| 32.Si se utiliza un nivel con visor, se puede
llevar a cabo un levantamiento radial (ver punto 34). Se coloca el nivel
en la EN1 y se efectúa una visual hacia atrás leyendo en dirección
al punto fijo de referencia (PF). Luego, se efectúa visuales hacia
adelante leyendo todos los puntos de la línea de base que sea posible.
A partir de esos datos se determina la altura del instrumento (HI) y la
altura de los puntos, con HI = H(PF) + VAt y H(punto) = HI � VAd. Cuando
es necesario se cambia la ubicación de la estación de nivelación
y se determina un nuevo HI en el último punto conocido, que se usa
como punto intermedio. A continuación se efectúa una serie
de visuales hacia adelante. Dado que las distancias de la cuadrícula
son fijas, no es necesario medirlas otra vez. Anote las medidas en un cuadro,
tal como se ve en el ejemplo. |
|
|
| |
|
|
|
Ejemplo
Levantamiento topogr�fico por cuadr�culas con un nivel con visor
|
Estaci�n de nivelado
|
Punto
|
RV
|
HI
|
VA
|
Altura
|
Comentarios
|
|
1
|
PF
|
1.53
|
101.53
|
-
|
100.00
|
Altura supuesta
|
| |
A1
|
-
|
101.53
|
1.25
|
100.28
|
|
| |
A2
|
-
|
101.53
|
1.20
|
100.33
|
|
| |
A3
|
-
|
101.53
|
1.15
|
100.38
|
|
|
2
|
A3
|
1.48
|
101.86
|
-
|
100.38
|
Punto intermedio
|
| |
A4
|
-
|
101.86
|
1.41
|
100.45
|
|
| |
...
|
...
|
...
|
...
|
...
|
|
| |
A9
|
...
|
...
|
...
|
...
|
|
|
5
|
A1
|
1.20
|
101.48
|
-
|
100.28
|
A partir del A1de arriba
|
| |
B1
|
-
|
101.48
|
0.23
|
100.25
|
|
| |
C1
|
-
|
101.48
|
0.25
|
100.23
|
|
| |
D1
|
-
|
101.48
|
0.28
|
100.20
|
|
|
6
|
D1
|
1.30
|
101.50
|
-
|
100.20
|
Punto intermedio
|
| |
E1
|
-
|
101.50
|
0.35
|
100.15
|
|
| |
...
|
...
|
...
|
...
|
...
|
|
| |
G1
|
-
|
101.50
|
0.47
|
100.03
|
|
|
9
|
A2
|
1.35
|
101.68
|
-
|
100.33
|
A partir del A2 de arriba
|
| |
B2
|
...
|
...
|
-
|
...
|
|
| |
...
|
...
|
...
|
...
|
...
|
|
|
12
|
F2
|
...
|
...
|
-
|
...
|
|
| |
G2
|
...
|
...
|
-
|
...
|
|
|
13
|
A3
|
...
|
...
|
-
|
100.38
|
A partir del A3 de arriba
|
| |
...
|
...
|
...
|
...
|
...
|
|
|
| |
Ejemplo
Levantamiento topogr�fico por cuadr�culas
con un nivel sin visor

|
| 33.Si se usa un nivel sin dispositivo visual, primero
se sigue la línea base AA. Utilizando el punto fijo como punto de
referencia, se lleva a cabo el levantamiento de todos los puntos A1, A2,
... A9. Luego se repite el procedimiento a lo largo de cada perpendicular,
comenzando con el punto de la línea base conocido, como punto de
referencia.
Se anotan todas las mediciones en un cuadro y se determina la altura
de cada punto de la cuadrícula (ver puntos 38-41 para una explicación
más detallada).
El cuadro prevé un espacio en la parte inferior para verificar
los cálculos y las mediciones (ver punto 41 en esta Sección).
|
|
|
Levantamientos
topográficos radiales
|
| 34. Para llevar a cabo un levantamiento radial (ver Sección
72), primero se debe determinar la altura del instrumento HI en la estación
de nivelación O. Se mira hacia el punto X de altura conocida H(X)
y se efectúa una medición de visual hacia atrás (VAt).
Se aplica:
35. Luego se debe determinar la altura de los puntos A, B, C y D. Se
mira sucesivamente hacia cada uno de ellos, efectuando una visual hacia
adelante (VAd). Se calcula su altura como H (punto) = HI � VAd.
36. Se anotan todas las mediciones en un cuadro. Dicho cuadro también
puede incluir datos planimétricos tales como azimut y distancias
horizontales. También se pueden usar dos cuadros diferentes tal
como se explicó en el punto 23. La primera línea del cuadro
se refiere el punto conocido X. Dicho punto puede ser uno de los puntos
del perímetro que ya ha sido determinado, o puede ser un
punto fijo (ver punto 42). Se determina la posición del punto
O a partir del azimut de la línea OX y la distancia horizontal
OX. |
|
Use X como punto de referencia

|
| |
|
|
|
|
| |
|
|
|
Ejemplo
Levantamiento topogr�fico radial
|
Estaci�n de nivelaci�n
|
Punto
|
RV
|
HI
|
VA
|
Altura (m)
|
Azimut (grados)
|
Distancia (m)
|
Comentarios
|
|
0
|
X
|
0.45
|
144.00
|
-
|
143.55
|
285
|
35.3
|
Altura conocida |
|
0
|
A
|
-
|
144.00
|
1.65
|
142.35
|
50
|
29.6
|
|
|
0
|
B
|
-
|
144.00
|
0.97
|
143.03
|
131
|
27.3
|
|
|
0
|
C
|
-
|
144.00
|
0.60
|
143.40
|
193
|
25.1
|
|
|
0
|
D
|
-
|
144.00
|
1.12
|
142.88
|
266
|
24.8
|
|
|
Combinación de los métodos de levantamiento
por poligonal y por radiación
|
37. Este método combina el levantamiento radial con
una poligonal cerrada. Se puede utilizar para reunir la información
necesaria para elaborar un plano topográfico de un terreno,
por ejemplo del emplazamiento de una granja acuícola (ver Capítulo
9). Aplicando los métodos de levantamiento topográfico ya
estudiados, se procede de la siguiente manera:
(a) a) Mediante una poligonal cerrada, se realiza el levantamiento planimétrico
del per�metro del �rea ABCDEA. Se determina
la longitud y la dirección de todos los lados (ver Sección
71). |
|
Fix the position of LS 1 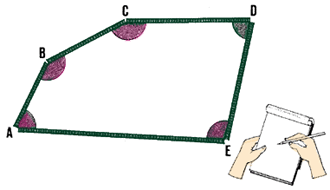
|
| |
|
|
| (b) En el interior del sitio, se seleccionan varias estaciones
de nivelación 1, 2, 3, ... 6, desde las cuales se puede realizar
el levantamiento radial de la superficie cercana. |
|
Choose levelling stations

|
| |
|
|
| (c) Se determina la posición de la estación
de nivelación 1 midiéndola en relación a los
puntos conocidos del perímetro tales como A y B. Se puede utilizar,
por ejemplo,la plancheta o proceder por triangulaci�n
(ver Sección 9.2). |
|
Survey the boundaries

|
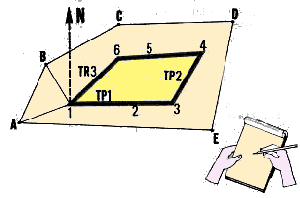
(d) Se unen todas las estaciones de nivelación seleccionadas,
mediante líneas rectas para formar una poligonal cerrada.
Se efectúa el levantamiento utilizando, si es necesario puntos
intermedios, para fijar la posición de cada estación
y para determinar su altura. Se verifica el error de cierre
(ver Sección 7.1) y esta Sección, punto 20).
|
|
Levantamiento de todas las estaciones de nivelaci�n
|
| |
|
|
| (e) A esta altura se puede iniciar el levantamiento topográfico
detallado, procediendo sucesivamente a partir de cada estación
de nivelación conocida. A partir de la estación 1, se traza
una serie de líneas rectas radiales a un intervalo fijo
de ángulo (tal como 20°). Esto significa que cada línea
radial está a 20° de la siguiente. Se usa la brújula
y jalones o estacas. Se marca sobre el terreno la línea norte-sur,
que también se puede llamar la línea cero grado.
De pie sobre esta línea en la estación 1, se mide y marca
una línea con un azimut de 20°. Luego, girando en el sentido
de las agujas del reloj, siempre en el mismo punto, se mide y marcan sucesivamente
líneas con azimut 40°, 60°, ... 340°.
Nota: el intervalo fijo de ángulo que se
debe usar depende de la precisión que se requiere. Valores angulares
más pequeños permiten establecer un mapa más preciso
del lugar.
|
|
Marque las l�neas radiales a los intervalos que ha elegido

|
| |
|
|
| (f) A partir de la estación 1, utilizando la nivelación
diferencial, se procede al levantamiento de una serie de puntos sobre
cada línea radial. Se puede elegir cualquier punto, por ejemplo la
intersección de la línea radial con el perímetro del
sitio, o un punto en el cual la pendiente del suelo cambia bruscamente,
o el emplazamiento de una roca o un árbol. Al mismo tiempo que se
determina la altura de tales puntos, se mide la distancia
entre cada uno de ellos y la estación de nivelación, de manera
tal que luego se los pueda transportar a un mapa. |
|
|
| |
|
|
| (g) Desplazándose sucesivamente a cada estación
(2, 3, 4, 5, 6), se repiten los puntos (e) y (f), midiendo la altura y la
distancia de puntos no conocidos elegidos al azar, ubicados sobre
las líneas radiales, de manera tal de establecer el nivel de toda
el área. |
|
|
| |
|
|
| (h) Se anotan todas las mediciones en un cuadro y se calcula
la altura de todos los puntos considerados (ver esta misma Sección,
punto 36). El cuadro requiere dos columnas adicionales:
|
|
|
| |
|
|
- una columna llamada �línea� en la cual se registran
los azimut de cada línea;
- una columna llamada �Distancias acumuladas�. En este espacio
se puede calcular separadamente la distancia desde la estación
de nivelación al punto considerado sobre cada línea radial.
|
|
|
| |
|
|
|
Ejemplo
Levantamiento topogr�fico radial compuesta de parte de un terreno

|
Levantamiento topográfico con un nivel sin visor
|
| 38. También es posible realizar levantamientos
topográficos a lo largo de líneas rectas utilizando niveles
sin visor, tales como el nivel de cuerda
(ver Sección 5.2) o el nivel de agua de tubo flexible (ver Sección
5.3). Ya se ha explicado cómo se procede para medir diferencias
de nivel por cuadrícula, con ese tipo de niveles (ver punto 33
de esta Sección).
Recuerde que cuando se traza la cuadrícula, la
distancia entre los puntos debe ser inferior a la longitud del nivel
utilizado.
|
|
|
| |
|
|
| 39. Este método requiere de un equipo de dos o tres
personas. El observador de atrás y el de adelante realizan las mediciones
en el campo, pero sólo una persona es la responsable de anotar tales
medidas en el cuaderno de campo. |
|
|
| 
|
| |
|
Ejemplo
Levantamiento topogr�fico con un nivel de cuerda (20 m)

|
40. Se registran las mediciones en un cuadro o tabla para cada sector estudiado.
Se miden distancias horizontales de un punto al siguiente y las diferencias
de nivel correspondientes. En los puntos inicial y final, se efectúa
una sola medición de altura. La persona de atrás realiza esa medición
en el punto inicial y la persona que va delante, en el punto final.
41. Se determinan las distancias acumuladas a partir del punto inicial y las
alturas de cada punto, como indica el ejemplo. Se pueden realizar tres verificaciones
en la parte inferior del cuadro.
Establecimiento
de puntos fijos de referencia para levantamientos topográficos
42. Como se acaba de explicar, la nivelación diferencial se inicia siempre
midiendo una altura en relación a un punto en el suelo de altura
conocida o supuesta. Tal punto se convierte en un punto fijo de referencia
(PF). La altura de ese punto fijo constituye la base para determinar la
altura de los otros puntos que se deben levantar en el área.
43. Un punto fijo de referencia tiene que ser permanente. Es necesario
establecer al menos un punto fijo de referencia, cerca del sitio donde se construye
una granja acuícola, para que sirva como punto u objeto de referencia
fijo. También es posible usar el punto fijo de referencia como punto
intermedio durante un levantamiento topográfico.
44. Un punto fijo de referencia debe ser un punto perfectamente definido,
fácil de encontrar y de reconocer. También debe ser fácilmente
accesible, para que se le pueda colocar una mira graduada. Es posible establecer
un punto fijo de referencia:
- sobre un piquete de madera o bambú, colocado cerca del lugar de
la construcción;
- clavando un clavo en un árbol o en un tronco de árbol, cerca
del nivel del suelo, de manera que el clavo permanezca en su sitio aun si
el árbol es abatido;
- fijando una varilla de hierro en un bloque de cemento cerca del nivel del
suelo;
- sobre objetos o estructuras permanentes, que no deban ser desplazados,
abatidos o modificados, tales como un puente, una roca grande o la pared de
un edificio.
Nota :es preferible pintar el punto fijo de referencia
o poner varias señales cerca de él, para mostrar su ubicación.
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
| 45. En general la altura del punto fijo H(PF) no se conoce
y hay que darle un valor supuesto. Una vez que se establece el primer punto
fijo de referencia que se va a utilizar en un proyecto de construcción,
se le asigna una altura igual a un número entero que resulte conveniente,
por ejemplo 100 m. El número elegido debe ser bastante grande, de
manera que ningún punto del área tenga una altura negativa.
Nota : en los ejemplos precedentes, se vio que
algunos levantamientos topográficos se refieren a puntos medidos
precedentemente. Esto quiere decir que las mediciones se basan en dichos
puntos. Tales puntos se convierten en puntos fijos intermedios de
referencia. Se determina su altura por nivelación y se transforman
en alturas conocidas.
|
|
|
8.2 Cómo
realizar la nivelación de un perfil
|
¿Cuál es el objetivo de la nivelación de
un perfil?
|
| 1. El objetivo de la nivelación de un perfil es determinar
los cambios de altura de la superficie del suelo, a lo largo de una línea
definida. (Ya se ha explicado en qué consiste la nivelación
de un perfil usado con el método de cuadrícula en la Sección
81, punto 31). La línea definida AB puede ser el eje de un canal
de alimentación de agua, de una fosa de drenaje, del dique de un
reservorio o de un estanque. Igualmente se puede tratar del lecho de un
río que atraviesa un valle, en el cual se quiere levantar una represa
o también puede ser una de las líneas perpendiculares a un
río, trazadas a través del valle, en el curso de un levantamiento
topográfico realizado para elegir el emplazamiento adecuado de una
granja acuícola. |
|
L�nea del terreno AB

|
| |
|
|
| 2. ormalmente, las mediciones realizadas en el curso de la
nivelación de un perfil se transportan al papel, para que adquieran
la forma de un diagrama o croquis, llamado gráfico. Éste muestra
las variaciones de altura en relación con las distancias horizontales.
Este tipo de gráfico se llama perfil del
terreno y las Secciones 95 y 96 indican cómo se realiza. |
|
Perfil AB

|
¿En qué
consiste la nivelación de un perfil?
|
| 3. Para nivelar un perfil, se debe determinar la altura
de una serie de puntos situados a intervalos reducidos a lo largo
de una línea definida. Tales alturas determinan el perfil
de la línea.
4. Existen dos tipos de perfiles comúnmente utilizados en piscicultura:
perfil longitudinal y sección transversal.
|
|
|
| |
|
|
- · El levantamiento de una sección transversal
se lleva a cabo en general, a lo largo de
una l�nea que es perpendicular a un perfil longitudinal ya estudiado,
usando los puntos de altura conocida como puntos fijos de referencia.
Definir la sección transversal de un valle, por ejemplo, puede
ser muy útil para ubicar un lugar adecuado para una granja de
peces. En una escala más reducida, también se puede llevar
a cabo el levantamiento de la sección transversal para canales
de alimentación de agua, construcción de represas o de
estanques. Ya se vio cómo se usan los perfiles de sección
transversal cuando se lleva a cabo un levantamiento con el método
de la cuadrícula (ver Sección 81, punto 31).
|
|
|
Levantamiento
de un perfil longitudinal con el método radial
|
| 5. Se debe realizar el levantamiento de la línea AB,
el eje de un canal de agua, aplicando el método radial y utilizando
un nivel con dispositivo visual. Se mide la distancia horizontal y se marca
la línea con estacas o jalones cada 25 m, desde el comienzo hasta
el final. Se añaden algunos puntos adicionales donde existen pronunciados
cambios de pendiente. En cada jalón se indica claramente la distancia
desde ese punto, hasta el punto inicial A, o sea la distancia acumulada. |
|
Marque con piquetes la l�nea

|
| |
|
|
| 6. Se coloca el nivel en EN1. Se efectúa una visual
hacia atrás, VAt, desde un punto fijo de altura H(PF) para determinar
la altura del instrumento HI, tal como:
|
|
Determine Hl y LS 1

|
| |
|
|
| 7. Desde la estación de nivelación EN1, se efectúan
visuales hacia adelante (VAd) dirigidas a tantos puntos (por ejemplo, seis)
de la recta AB como sea posible, comenzando con el punto inicial A. |
|
Efectue visuales hacia los puntos que se han marcado

|
|
8. Cuando es necesario se desplaza el nivel hacia una nueva estación,
para seguir leyendo los puntos siguientes, teniendo en cuenta que:
- primero, se debe elegir un punto intermedio PI y efectuar
una visual hacia atrás, VAt, para determinar su altura a partir
de EN1;
- el observador se desplaza hacia la próxima estación
de nivelación, EN2, desde la cual puede ver el punto intermedio,
PI;
- el observador efectúa una visual hacia atrás, VAt,
en ese punto intermedio para determinar la nueva altura del instrumento,
HI.
|
|
Haga una lectura de mira hacia adelante
desde LS 1 hacia el punto intermedio

|
| |
|
|
| 9. A continuación se llevan a cabo visuales hacia adelante,
VAd, dirigidas a tantos puntos como es posible, hasta alcanzar el punto
final de la recta AB. Si es necesario, se usa otro punto intermedio y una
nueva estación de nivelación, tal como se ha descrito en el
punto 8. |
|
Haga una lectura de mira hacia atr�s
desde LS 2 hacia el punto intermedio

|
| |
|
|
| 10. Todas las mediciones se anotan en el cuaderno de campo,
utilizando un cuadro similar a los que se usaron con los otros métodos.
Se determinan las alturas de los puntos (excepto de los puntos intermedios)
restando cada visual hacia adelante, VAd, de su correspondiente HI. En el
ejemplo que se da en esta página, la distancia horizontal acumulada
(en metros) aparece en la primera columna como la numeración de los
puntos: 00, 25, 50, 65, etc.
|
|
Haga lecturas de mira hacia
los puntos que se han marcado

|
| |
|
|
|
Ejemplo
Levantamiento radial de perfil longitudinal con nivel con visor
|
Puntos (m)
|
RV
|
HI
|
VA
|
Altura(m)
|
Comentarios
|
|
PF
|
1.37
|
2.87
|
-
|
1.50
|
Clavar al pie del tronco del �rbolp |
|
00
|
-
|
2.87
|
1.53
|
1.34
|
Inicio del canal |
|
25
|
-
|
2.87
|
1.67
|
1.20
|
|
|
50
|
-
|
2.87
|
1.73
|
1.14
|
|
|
65
|
-
|
2.87
|
1.90
|
0.97
|
Cambio de pendiente marcada |
|
75
|
-
|
2.87
|
2.05
|
0.82
|
|
|
100
|
-
|
2.87
|
2.22
|
0.65
|
|
|
TP
|
1.80
|
3.07
|
1.60
|
1.27
|
Sobre piedra |
|
125
|
-
|
3.07
|
2.27
|
0.80
|
|
|
150
|
-
|
3.07
|
2.37
|
0.70
|
|
|
175
|
-
|
3.07
|
2.57
|
0.50
|
|
|
200
|
-
|
3.07
|
2.77
|
0.30
|
|
|
230
|
-
|
3.07
|
3.00
|
0.07
|
Final del canal |
|
Levantamiento de un perfil longitudinal
por poligonal
|
| 11. Se debe llevar a cabo el levantamiento de la misma
recta AB, el eje de un canal de agua, para establecer su perfil. Se usa
un nivel sin dispositivo visual, tal como un nivel de agua de tubo flexible (ver Sección
5.3). Dado que se usa este tipo de nivel, se procede a un levantamiento
por poligonal. Se marca la línea AB clavando jalones
en el suelo a intervalos regulares. La longitud de los intervalos depende
del largo del nivel (en este caso, 10 m). Se agregan jalones intermedios
cuando aparecen cambios de pendiente muy marcados. En cada jalón
se marca su distancia en relación al punto inicial A.
12. Nivele una línea de unión entre el punto fijo de referencia
PF y el punto inicial A ver Secci�n
53, puntos 6-12). Esta operación permite conocer la altura
del punto A, mediante el punto intermedio 1.
|
|
Marque la l�nea a intervalos de 10 m

|
| |
|
|
| 13. Proceda al levantamiento de los puntos
marcados a lo largo de la recta, usando el método indicado. En
cada punto se deben efectuar dos lecturas de escala, una hacia atrás
y una hacia adelante, excepto en el punto final en el cual se realiza
solo una medición de altura.
14. Una sola persona debe ser la responsable del registro de las
mediciones en el cuaderno de campo, utilizando un cuadro semejante
al que aparece en la Sección 81, punto 41. Pero en este caso no
es necesario anotar las distancias en el cuadro, ya que ellas identifican
los puntos objeto del levantamiento. Las verificaciones se realizan en
la parte inferior del cuadro, como es habitual. Recuerde que este tipo
de levantamiento se realiza sin puntos intermedios.
|
|
Nivele el punto de enlace
desde el punto fijo de referencia (PF)
y nivele despu�s los puntos de la l�nea que los une

|
| |
|
|
|
Ejemplo
Levantamiento por poligonal de un perfil con un nivel de tubo flexible (10 m)

|
Levantamiento de la secci�n transversal
|
15. Después de haber determinado la altura de los puntos del perfil
longitudinal, se procede al levantamiento de las secciones transversales
perpendiculares. Estas secciones transversales pueden pasar
por tantos puntos como sea necesario, y en general son útiles para
establecer curvas de nivel en terrenos largos y estrechos (ver Sección
83).
16. Será necesario recoger mayor información sobre algunos
puntos del perfil longitudinal. Se eligen dichos puntos y se marcan. Luego
se trazan y marcan l�neas perpendiculares
a tales puntos (ver Sección 3.6); se prolongan dichas perpendiculares,
tanto como sea necesario, a ambos lados de la poligonal. En
este tipo de nivelación, tales perpendiculares se llaman las rectas
de la sección transversal.
|
|
|
| |
|
|
| Nota : en los puntos en los cuales la
poligonal cambia de dirección (por ejemplo, el punto 175 del dibujo),
es necesario trazar dos perpendiculares, E y F; cada una de estas líneas
es perpendicular a una sección de la poligonal. |
|
Haga dos secciones transversales en cada cambio de direcci�n

|
| |
|
|
|
17. Se eligen y se marcan claramente los puntos de cada recta de sección
transversal que se quieren medir. En este caso, los puntos no tienen que
estar a una distancia regular unos de otros. Más bien, es preferible
que estén ubicados donde el terreno presenta modificaciones,
que pueden corresponder a cambios de pendiente.
18. Como ya se conoce la altura de los puntos de la poligonal, a partir
de un estudio preliminar, se los considera como puntos fijos. Se procede
con el levantamiento del perfil de puntos seleccionados a lo largo de
las rectas de sección transversal, tal como se explicó previamente.
A tal efecto, se realiza el levantamiento:
Nota : también se puede proceder por poligonal
utilizando un un nivel visual simple ,como el nivel de bambú
(ver Sección 56) o un nivel de mano (ver Sección 5.7).
|
|
|
19. Las notas tomadas en el campo resultarán semejantes a las indicadas
en los puntos 10 ó 14, dependiendo del método de nivelación
utilizado. De todos modos, la identificación de los puntos es distinta.
En efecto, se identifica cada recta de sección transversal por el
número correspondiente al punto de la poligonal de altura conocida.
Para hacer esto, se identifican los puntos medidos de cada recta según
se encuentren a la izquierda o a la derecha de la poligonal. Se completa
la identificación con la distancia (en metros) medida desde el punto
de la poligonal. El ejemplo a continuación presenta las notas tomadas
en el campo y los cálculos efectuados durante un levantamiento radial,
en el cual cada recta de sección transversal ha sido medida desde una
única estación de nivelación.
|
Ejemplo
Nivelaci�n radial de un corte transversal
|
Punto de la poligonal
|
Punto
|
RV(m)
|
HI(m)
|
VA(m)
|
Altura(m)
|
Comentarios
|
| |
Derecha
|
Izquierda
|
|
|
|
|
|
|
50
|
...
|
...
|
...
|
...
|
...
|
...
|
|
|
75
|
-
|
-
|
0.54
|
40.94
|
-
|
40.40
|
Borde del camino existente
|
| |
10
|
-
|
|
40.94
|
1.09
|
39.85
|
|
| |
18
|
-
|
|
40.94
|
1.15
|
39.79
|
|
| |
-
|
9
|
|
40.94
|
0.85
|
40.09
|
|
| |
-
|
16
|
|
40.94
|
0.68
|
40.26
|
|
|
100
|
-
|
-
|
1.15
|
38.96
|
-
|
37.81
|
Borde del campo de ma�z
|
| |
8
|
-
|
|
38.96
|
1.23
|
37.73
|
|
| |
-
|
4
|
|
38.96
|
1.11
|
37.85
|
|
| |
-
|
16
|
|
38.96
|
0.78
|
38.18
|
|
|
125
|
-
|
-
|
0.97
|
36.64
|
-
|
35.67
|
Borde de un bosquecillo
|
| |
5
|
-
|
|
36.64
|
1.12
|
35.52
|
|
| |
20
|
-
|
|
36.64
|
1.55
|
35.09
|
|
| |
-
|
14
|
|
36.64
|
1.03
|
35.61
|
|
| |
|
25
|
|
36.64
|
0.89
|
35.75
|
|
|
150
|
...
|
...
|
...
|
...
|
...
|
...
|
|
|
8.3
Cómo trazar curvas de nivel
|
¿Qu� es una curva de nivel?
|
| 1. Una curva de nivel es una línea recta
o curva, imaginaria y continua, que une puntos del terreno que tienen la
misma altura. La altura de tales puntos debe ser medida en relación
al mismo plano de referencia. |
|
|
| |
|
|
|
Ejemplo
Si se vierte agua en un hueco del terreno, es posible observar que
la superficie del agua forma una línea continua constituida por
los puntos en los cuales el agua está en contacto con los costados
del hueco. Esa línea define la curva de nivel que corresponde a
esa altura de agua en el hueco. Un lago o un reservorio también
definen una curva de nivel correspondiente a la superficie, que depende
del nivel del agua. |
|
|
| |
|
|
¿En qué consiste el trazado de curvas de
nivel?
|
|
2. Trazar curvas de nivel consiste en identificar dichas curvas en el
terreno, marcarlas con jalones y transportarlas a un mapa o plano
La Secci�n 9.4 ofrece informaci�n adicional
sobre el dibujo de curvas de nivel en mapas y planos.
|
|
|
| 3. El trazado de curvas de nivel se usa en acuicultura
para resolver dos tipos de problemas:
- si ya se ha decidido la ubicaci�n de un punto, puede ser necesario
identificar la curva de nivel que pasa por ese punto;
Ejemplo
Se ha elegido el punto de llegada de un canal de alimentación
de agua, en una granja acuícola. A continuación se debe
determinar el eje del canal, que generalmente describe una curva de nivel,
remontándose hasta la fuente de suministro del agua (que puede
ser un punto a lo largo del río, o la tubería de salida
de una bomba). |
|
|
| |
|
|
|
- si se debe dibujar un plano o mapa que muestre el relieve del terreno,
es necesario determinar la ubicación de las curvas en el terreno
para poderlas transferir luego al papel.
Ejemplo
Se ha elegido el emplazamiento de una granja acu�cola. Para poder
planificar, dise�ar y construir la granja, es necesario previamente realizar
un mapa topogr�fico que muestre la localizaci�n de una serie de curvas
de nivel, a partir de las cuales se conoce el relieve del terreno.
|
|
|
| |
|
|
|
4. si se debe dibujar un plano o mapa que muestre
el relieve del terreno, es necesario determinar la tubicaci�n
de las curvas en el terreno, para poderlas transferir luego al papel.
5. En las siguientes secciones se estudia cómo realizar el levantamiento
de curvas de nivel en el terreno, para luego preparar un mapa topográfico
(ver Sección 94).
|
|
|
| |
|
|
|
¿Cuáles son los principales métodos de levantamiento de
curvas de nivel?
|
|
6. La determinación de todas las curvas de nivel de un terreno
es una tarea imposible. Por lo tanto, es necesario decidir cuántas
curvas de nivel se deben identificar en cada área. En tal caso,
se fija la diferencia de nivel entre curvas cercanas, que se llama
intervalo de curvas de nivel.
7. La elección del intervalo que se va a usar depende sobre todo
de la precisión que se requiere, de la escala en la cual se debe
dibujar el plano (ver Sección 91) y del tipo de terreno que es
objeto del levantamiento. Los intervalos de curvas de nivel en general
varían de 0,25 m a 1 m. Este rango de intervalos asegura
una buena precisión, permite dibujar mapas topográficos
a gran escala de áreas planas o con una ligera pendiente (como
son los terrenos que se eligen para construir granjas acuícolas).
Dado que los intervalos menores hacen muy difícil el trazado de
curvas de nivel, en general las prospecciones y los estudios preliminares
se llevan a cabo con un intervalo de curvas de nivel mayor que el usado
posteriormente para levantamientos más detallados.
|
|
|
| |
|
|
|
Ejemplo
Relaciones existentes entre el tama�o de las curvas de nivel y algunos factores
|
Factor
|
Intervalos entre curvas de nivel
|
|
M�s peque�o
|
M�s grande
|
| Precisión requerida |
Alta
|
Baja
|
| Escala del mapa (Sección 9.1) |
Escala grande
|
Escala pequeña
|
| Tipo de terreno |
Plano
|
Inclinado
|
|
|
|
| |
|
|
| 8. Existen dos métodos principales
de trazado de curvas de nivel:
- un método directo, por el cual se trazan y marcan
la línea que sigue cada curva de nivel en el terreno, y luego
se realiza el levantamiento planimétrico de dichas líneas
para poder representarlas en un mapa;
- un método indirecto, por el cual se realiza un
levantamiento topográfico del área para determinar una
serie de puntos de altura conocida. Luego se los representa en el plano
y se determina la curva de nivel a partir de ese plano.
|
|
Trazado directo de curvas de nivel

|
| |
|
|
Elección de un método de levantamiento
de curvas de nivel
|
|
|
| 9. Cuando se selecciona el método que se va a usar
para trazar curvas de nivel, es importante recordar que:
- el método directo es más lento, pero más
preciso. Es preferible usarlo para trazar curvas en un área relativamente
pequeña que se debe estudiar en detalle, a una escala grande;
- el método indirecto es más veloz, pero no
tan preciso. Se usa para trazar curvas en áreas grandes que luego
se transfieren al plano en pequeña o media escala. Es preferible asociarlo con el uso de la plancheta
(ver Secci�n 75).
|
|
ITrazado indirecto de curvas de nivel

|
Trazado de curvas de nivel en
el terreno con un nivel con dispositivo visual
|
|
A continuación se explica el método directo de trazado
de curvas de nivel que permite determinar una serie de puntos en el suelo
que tienen exactamente la misma altura.
10. Se inicia el trazado de curvas de nivel del sitio ABCDEA en un punto
de altura conocida, tal como un punto fijo de referencia ya existente,
PF .Si no existe tal punto en el área,
se puede establecer:
- mediante nivelación diferencial a partir de un
punto fijo de referencia fuera del área, en dirección
a un punto dentro del área; o también
- suponiendo una altura conveniente para el punto fijo (tal
como 100 m), de manera que ningún punto considerado sucesivamente
resulte con una altura negativa.
Nota : es preferible que el punto fijo de referencia
quede establecido en el medio de la parte más baja del terreno,
de manera que el levantamiento se pueda realizar cuesta arriba.
|
|
Establezca un punto fijo de referencia (PF)
en la parte mas baja de la parcela

|
| |
|
|
| 11. A partir del punto fijo de referencia PF,
en el punto F, trace y marque la línea recta FG. Asegúrese
que la recta sigue la dirección de la pendiente más
pronunciada del terreno. La recta debe atravesar toda el área.
12. Trace una, serie de l�neas paralelas a FG. a intervalos regulares.
Para elegir el intervalo entre las paralelas, use:
- 10 m o menos, si el intervalo de curvas de nivel debe
ser de 0,25 a 0,50 m;
- 25 a 30 m, si el intervalo de curvas de nivel debe ser
de 1 a 1,50 m;
- 50 m, si el terreno tiene una pendiente muy suave o regular.
|
|
Trace la l�nea FG desde el punto fijo de referencia (PF)
y l�neas paralelas a intervalos regulares

|
| |
|
|
| 13. Si se conoce la altura H(PF) del punto fijo de referencia
PF, a partir de una prospección anterior, primero se determina un
punto de la recta que tenga un altura correspondiente a un múltiplo
del intervalo de curva de nivel elegido. Se puede usar un nivel
con dispositivo visual junto con una mira
graduada de tablilla. De esta manera, es posible fijar la tablilla en
la mira a la altura requerida para identificar la primera curva de nivel
en el terreno. |
|
Establezca una visual hacia atr�s hacia el punto fijo de referencia
(PF) y calcule la curva de nivel mas cercana

|
| |
|
|
|
Ejemplo
- PF está a una altura de 59,36 m.
- Con el nivel con dispositivo visual instalado en la EN1 y la mira
graduada colocada en PF, se efectúa una VAt = 3,23 m.
- Se elige el intervalo de curva de nivel, por ejemplo IC = 0,25 m.
- Se calcula el múltiplo de IC (= nIC) más cercano a
H(PF) = 59,36 m, de la siguiente manera:
a) H(PF) ÷ IC = 59,36 m ÷ 0,25 m = 237,44 .. o el número
redondo n = 238;
b) n x IC = 238 x 0,25 m = 59,50 m.
- La diferencia entre H(PF) y n(IC) es igual a 59,50 m � 59,36 m =
0,14 m.
- Coloque la tablilla en la mira graduada a la altura de VAt menos
esa diferencia, o sea 3,23 m � 0,14 m = 3,09 m.
- Determine la posición de la primera curva de nivel a la altura
59,50 m.
|
|
Coloque la mira de tablilla en H(BM) - n(CL)
por debajo de la l�nea de mira

|
| |
|
|
| |
|
Cuando la mira de tablilla est� en la l�nea de miraquiere decir
que se ha encontrado un punto de la primera curva de nivel

|
| 14. Este método exige el concurso de un asistente.
En EN1, desde donde es posible observar la mayor cantidad de puntos vecinos,
se instala el nivel. Sosteniendo la mira graduada con la tablilla ya
ajustada, el asistente remonta lentamente la pendiente, a partir del
punto fijo recorriendo el eje FG. El operador mira hacia la tablilla
con el nivel y le dice al asistente que se detenga cuando la línea
visual coincide con la tablilla. El punto en el terreno X donde le encuentra
la mira graduada debe estar a una altura de 59,50 m. Ese es el primer punto
de la curva de nivel de 59,50 m. El operador indica al asistente que marque
el punto con un jalón. Es importante indicar claramente en el jalón
la altura del punto.
|
|
Marque el punto

|
| |
|
|
| 15. El asistente se desplaza llevando la mira graduada hacia
otra línea paralela, donde se determina y marca un segundo punto
Y, siempre a la altura de 59,50 m, siguiendo el mismo procedimiento. Se
repite la operación en todas las líneas paralelas, hasta que
la curva de nivel de 59,50m ha sido completamente marcada en el suelo, a
lo largo de toda el área. |
|
Haga el levantamiento de otros puntos de la misma curva de nivel

|
| |
|
|
|
16. Para determinar la siguiente curva de nivel, se debe cambiar la posición
de la tablilla en la mira. Como se procede remontando la pendiente,
y se usa un intervalo de curva de nivel de 0,25, se debe bajar la
tablilla 25 cm, o sea 3,09 m � 0,25 m = 2,84 m. En esta posición,
la tablilla indicará puntos en el suelo que tengan una altura de
59,50 m + 0,25 m = 59,75 m, si se sigue midiendo a partir de la misma
estación de nivelación EN1.
|
|
Baje la mira de tablilla de acuerdo con el intervalo seleccionado

|
| |
|
|
|
17. A partir de EN1, se determinan todos los puntos de las líneas
paralelas que tienen una altura de 59,75 m y se marca una segunda curva
de nivel en el suelo. Nuevamente se baja la tablilla otros 0,25 m,
hasta una altura de 2,84 m � 0,25 m = 2,59 m para determinar los puntos
que están en la curva de 60 m.
|
|
Haga el levantamiento de la siguiente curva de nivel

|
| |
|
|
|
18. Si es necesario cambiar la estación de nivelación pero
se sigue midiendo la misma curva:
- se pide al asistente que sostenga la mira graduada en uno de los
puntos de la curva;
- se mueve el nivel hacia una nueva y más conveniente estación
de nivelación;
- se le dice al asistente que ajuste la altura de la tablilla hasta
que quede alineada con la línea visual del nivel;
- se continúa el levantamiento de la misma curva de nivel.
|
|
Para seguir en la misma curva de nivel, mueva
el nivel y ajuste despu�s la mira de tablilla

|
| |
|
|
|
19. Si es necesario cambiar la estación de nivelación,
al mismo tiempo que se inicia el trazado de una nueva curva
- se pide al asistente que sostenga la mira graduada en un punto de
la curva que se acaba de medir;
- se mueve el nivel hacia la nueva estación;
- se ajusta la altura de la tablilla con la nueva línea visual;
- se cambia la altura de la tablilla para determinar la nueva curva
de nivel (bajándola 0,25 m, por ejemplo, ver punto 16).
|
|
Para una nueva curva de nivel,
coloque la mira de tablilla por debajo de la l�nea de mira

|
| |
|
|
| |
|
Localice la nueva curva de nivel

|
20. Una vez determinada la intersección de las varias curvas de nivel
con cada línea paralela, se deben medir las distancias horizontales entre
todos los puntos marcados. Para hacer esto, se puede proceder por encadenado
a lo largo de las l�neas paralelas, comenzando
por los límites del área (ver Sección 26). Estas mediciones
permiten el posterior establecimiento del mapa topográfico del sitio
(ver Sección 9.4).
Mida la distancia horizontal entre los puntos
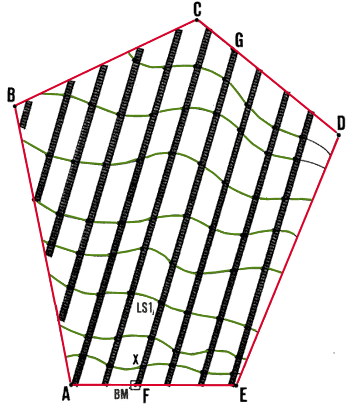
|
|
Trazado de curvas de nivel con un nivel sin visor
|
|
21. Si se utiliza un nivel sin visor (tal como un nivel de cuerda o un
nivel de bastidor en forma de A) para trazar curvas de nivel en un terreno,
la primera cosa que se debe hacer es establecer un punto
fijo de referencia PF, cerca del límite del área. Como
de costumbre, el punto fijo de referencia puede ser un punto de altura
conocida o de altura supuesta. Se debe situar en la zona más baja
del terreno (ver Sección 81, puntos 42-44).
22. Trace una línea FC a partir del PF, y trace líneas
paralelas a esta recta a una distancia determinada, tal como se
ha descrito en los puntos 11-12 más arriba.
Ejemplo
Distancia determinada para las paralelas = 10 m.
|
|
Trace una l�nea a trav�s del punto fijo de referencia
(PF) y paralelas a intervalos regulares

|
| |
|
|
|
23.. Si se utiliza un punto fijo de referencia de altura conocida,
se procede como se ha indicado en el punto 13 para calcular la altura
de la primera curva de nivel que se determina, cerca del punto fijo de
referencia. También se calcula la diferencia entre la altura de
esta primera curva y la altura del punto fijo de referencia.
Ejemplo
- Altura del PF, H(PF) = 127,85 m
- Intervalo de curva de nivel elegido = 0,50 m
- M�ltiplo de H(PF) = 127,85 m � 0,50 m = 255,70, por lo tanto
se elige n= 256
- La primera curva de nivel estar� a un altura de 256 x 0,50 m
= 128 m
- Diferencia de altura entre H(curva) y H(PF) = 128 m - 127,85
= 0,15 m.
|
|
Calculate the nearest contour line

|
| |
|
|
|
24. Cerca del punto fijo de referencia se colocan algunos objetos (tales
como ladrillos, piedras, planchas de madera, una lata o una caja) para
representar físicamente la altura de la primera curva de nivel
calculada.
|
|
Halle la diferencia de altura

|
| |
|
|
|
Ejemplo
Cerca de PF, coloque algunos ladrillos y ajuste su parte superior
a una altura de 0,15 m por encima de H(PF), usando
una regla y un nivel de alba�il (ver Secci�n 5.1). La parte
superior de estos ladrillos estará a un altura de 128 m. |
|
Use ladrillos para compensar la diferencia
de altura en el punto fijo de referencia (PF)

|
| |
|
|
| 25. Determine un punto en el suelo X, cerca de PF y situado
sobre la línea CF que pasa por PF, y que tiene la misma altura
que los objetos colocados cerca de PF. Para hacer esto, use alguno de
los métodos descritos antes (ver Secciones 51, 62-64 y 66). Este
punto del suelo X es el primer punto de la curva de nivel 128 m.
Ejemplo
Usando un nivel de regla, transfiera la altura 128 m desde la parte
superior de los ladrillos al punto en el suelo X, sobre la línea
CF, pasando por PF.. |
|
Localizaci�n de una curva de nivel a partir de
un punto
fijo de referencia (PF) de altura conocida

|
| |
|
|
|
26. Si se usa un punto fijo de referencia con una altura supuesta
y se trabaja cuesta arriba, determine el punto X de la línea que
pasa por PF del mismo modo. La altura de ese punto será igual a
la altura supuesta H(PF) más el intervalo de curva de nivel IC.
Ejemplo
- Si H(PF) = 100 m y IC = 0,50 m, significa que la altura de los
ladrillos es 0,50 en PF.
- Marque el sitio del punto cercano X en el cual H(X) = 100 m +
0,50 m = 100,50 m.
|
|
Localizaci�n de una curva de nivel a partir de
un punto
fijo de referencia (PF) al que se ha asignado una altura determinada

|
|
27. Inicie el trazado de la curva de nivel a partir del punto X usando
uno de los m�todos descritos en el Cap�tulo 6. Marque con un
jalón, cada punto donde la curva de nivel que se está
trazando cruza una de las líneas paralelas. En cada
jalón se debe indicar claramente la altura del punto al suelo.
28. Cada vez que se concluye el trazado de una curva, se determina el
primer punto, Z, de la curva siguiente usando un método similar
al descrito en el punto 24. En el punto conocido X, donde la última
curva de nivel cruza la línea central CF, se colocan objetos
cuya altura total es igual al intervalo de curva de nivel. Se transfiere
ese nuevo nivel horizontalmente a lo largo de la línea CF al punto
Z de la próxima curva de nivel. Si el intervalo es grande, es necesario
usar puntos intermedios y proceder por etapas.
|
|
Marque las intersecciones la curva de nivel con las paralelas

|
| |
|
|
|
Ejemplo
- IC = 0,50 m
- Transfiera la primera H(curva) mediante + 0,25 m, de X a Y.
- Repita nuevamente de Y a Z, para totalizar + 0,50 m = 2 x 0,25
m.
29. Una vez marcadas todas las curvas con jalones sobre el terreno,
se miden las distancias horizontales a lo largo de las l�neas paralelas
Esto facilita la preparación de un mapa topográfico (ver
Sección 9.4).
|
|
Transfiera la altura del intervalo de la curva de nivel

|
| |
|
|
| |
|
Mida las distancias horizontales entre los puntos

|
| |
|
|
Trazado de curvas de nivel con el
método indirecto
|
| 30. También es posible trazar curvas de nivel usando
un método indirecto. En este caso se realiza un levantamiento topográfico
del área, usando un patrón definido, tal como:
- una cuadrícula, para determinar la altura de los
puntos ubicados en las intersecciones de la cuadrícula constituida
por parcelas cuadradas o rectangulares;
- radial, para determinar la altura de puntos elegidos al
azar, localizados en líneas radiales que parten de un punto conocido
y se encuentran a un intervalo de ángulo definido;
- sección transversal, para determinar la altura
de puntos situados sobre líneas rectas cortas trazadas perpendicularmente
a una línea base conocida.
|
|
Cuadr�cula
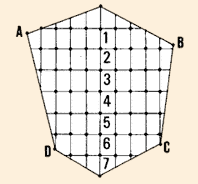
|
| |
|
|
| 31. Ya se vio que la cuadr�cula
se usa comúnmente para trazar curvas de nivel en áreas
relativamente pequeñas, en especial si el perímetro ya ha
sido nivelado (ver Sección 81, puntos 24-33).
32. También se estudió el modelo radial , que es especialmente útil
en áreas grandes (ver Sección 81, puntos 34-36).
|
|
Radiaci�n

|
| |
|
|
| 33. Finalmente se consideró la sección
transversal. Este tipo de procedimiento se usa normalmente en prospecciones,
cuando se requiere un plano de curvas de nivel de una franja larga y estrecha
de terreno para elegir el trazado más adecuado para nuestros propósitos.
Se trazan líneas a una distancia de 30 a 100 m y de unos 50 a 100
metros de largo a cada lado de la poligonal principal, y perpendiculares
a ella. Sucesivamente se determina la altura
de los puntos a los largo de la secci�n transversal (ver Secci�n 82, puntos
15-19). |
|
Secciones transversales
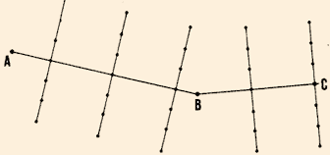
|
